野鸡题手写题解整合

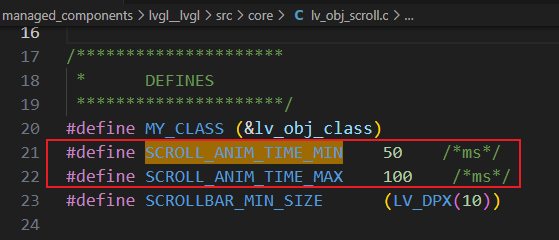
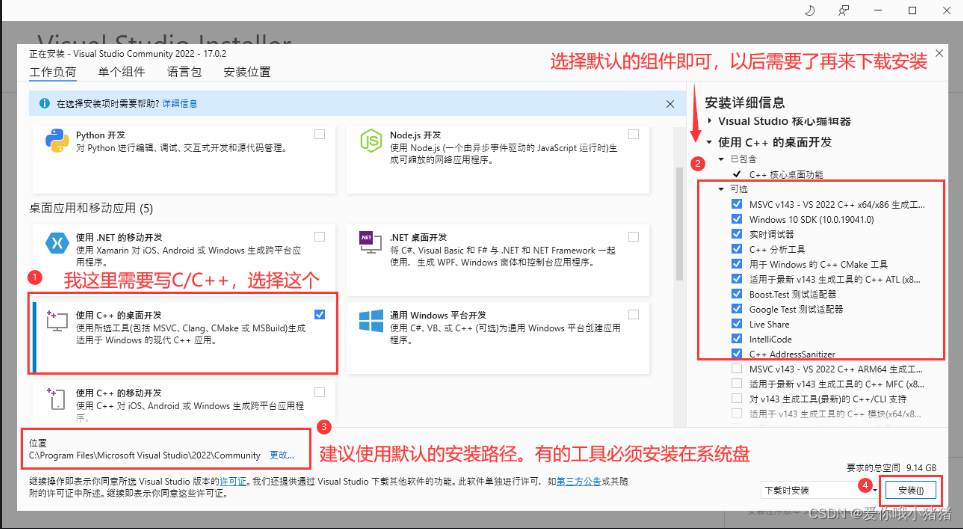
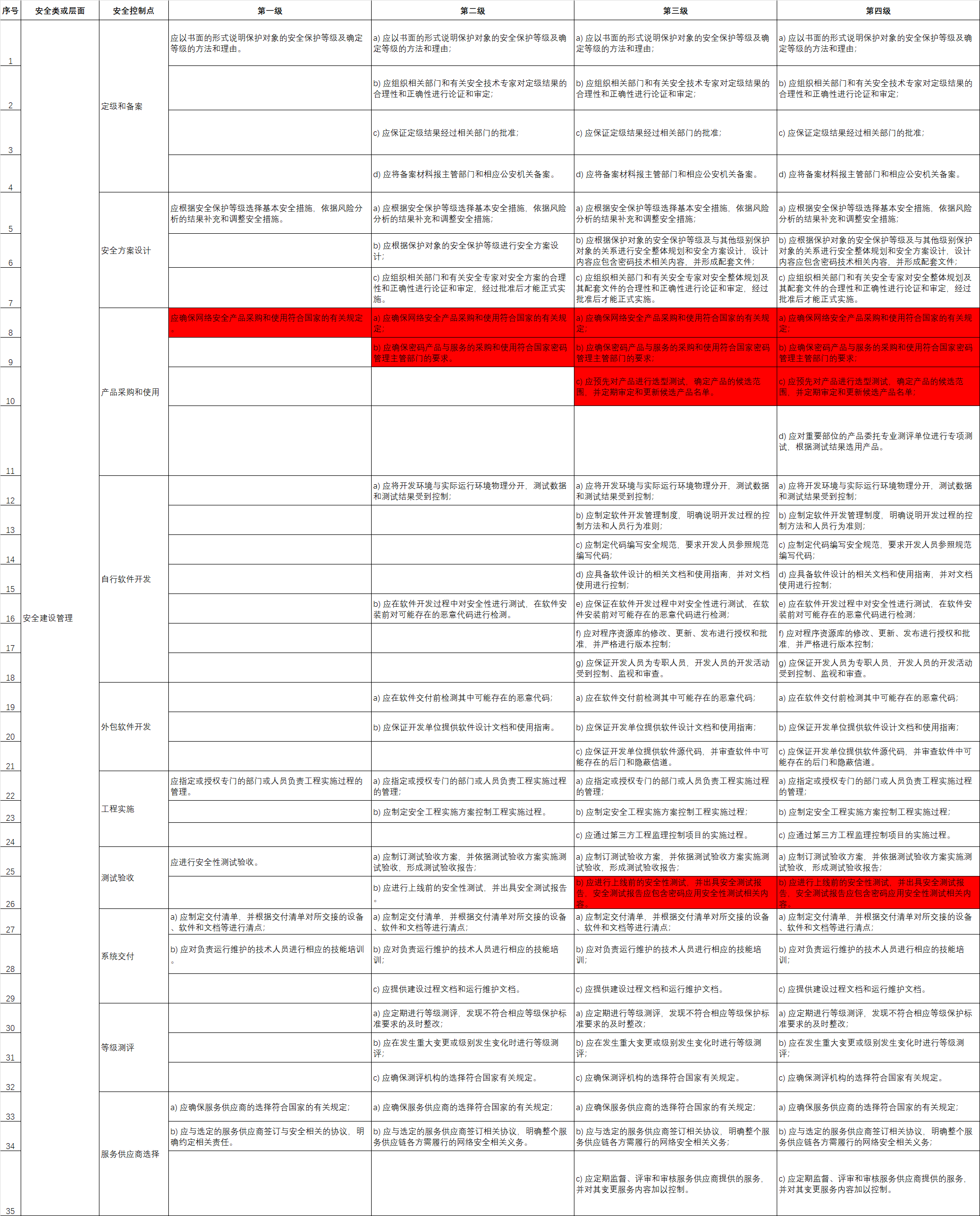
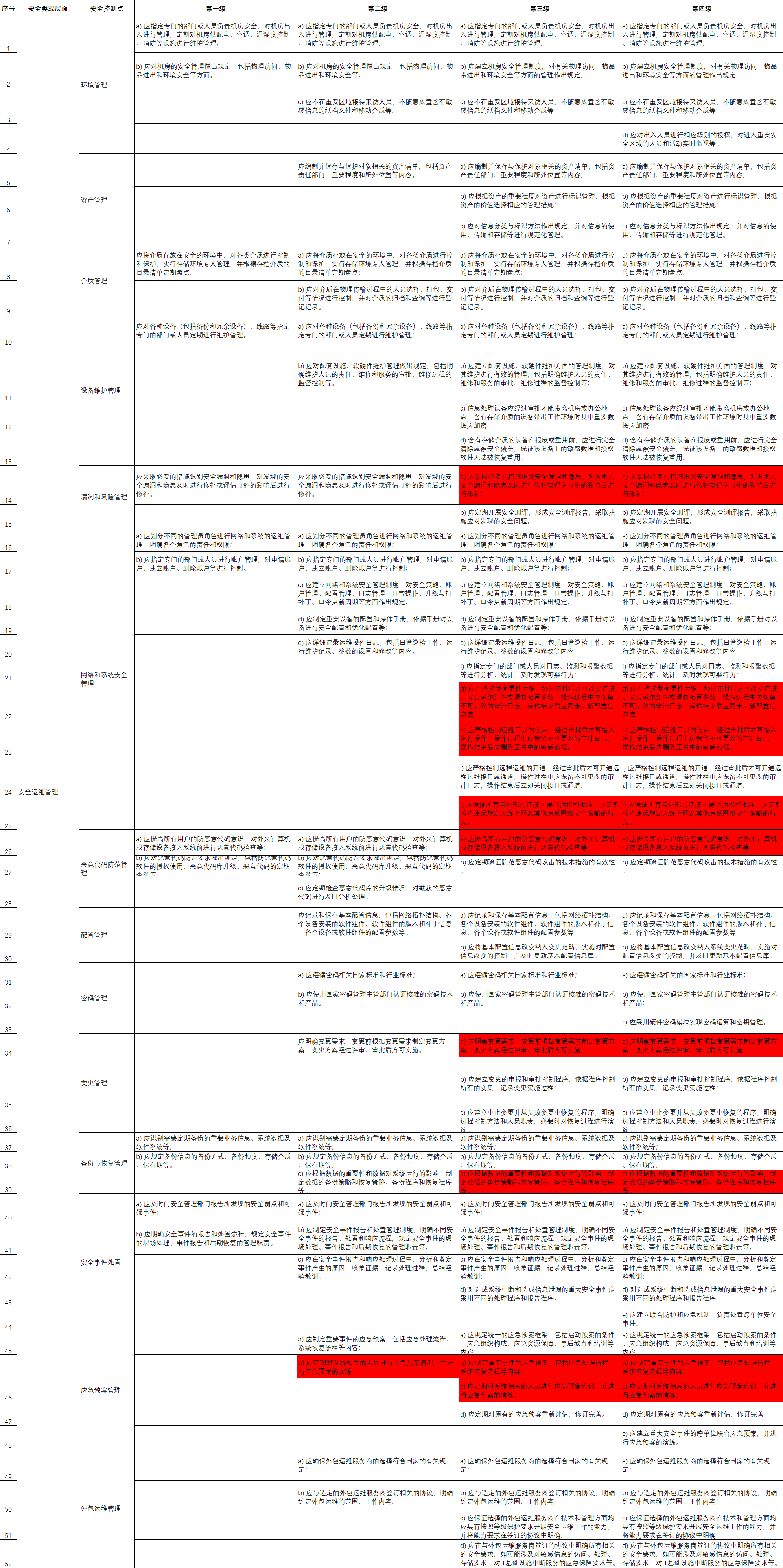
浴谷正在蒸蒸日上，专栏区怕是马上要倒闭了。

CF2026F

题 题。题外话：这场有点水平，E 题让我重拾了最大权闭合子图的记忆。

首先考虑没有这个可持久化（只有 \(2,3,4\) 操作）怎么做。\(0/1\) 背包问题，动态维护当前的 dp 数组 \(f_i\) 表示总体积 \(\sum p\) 不超过 \(i\) 的前提下，总价值 \(\sum t\) 的最大值，\(f\) 大小为值域 \(V=2000\)。不方便撤销的滑动窗口，自然想单调队列，但是 \(f\) 这个东西不符合单调队列的底层逻辑“更靠前且更小的元素没用”，因为每个物品的贡献不是简单的取 \(\max\)。

考虑如果把滑动窗口换成栈（要求 \(\mathcal O(V)\) 将某个元素压入栈或弹栈、给出体积限制 \(p\) 查询最大价值和），就可以直接做，对栈内每个物品维护它到栈底的所有物品构成的 \(f\) 即可。回到队列，引入普及组算法——双栈模拟队列就能够把问题规约到栈上。具体地，开前后两个栈 \(L,R\)，入队压入 \(R\)，出队时若 \(L\) 为空则把 \(R\) 中元素全部搬到 \(L\)，然后从 \(L\) 弹出。显然均摊 \(\mathcal O(1)\)。

回到原问题，暴力可持久化不能接受（修改量总共 \(\Theta(qV)\)，多不了 \(\log\)）。这类可持久化问题在操作可逆的情况下可以建出版本依赖树离线处理，对于本题，对 \(2,3\) 操作同样新建版本。考虑逆操作，要支持 pop_back 和 push_front，也就是把上文队列换成双端队列。双栈模拟仍然正确（插入删除都在对应一边，删除时如果那边的栈空了就把另一个栈全倒腾过来），不过复杂度是假的（多次 push_back 然后 pop_front 和 pop_back 交错能卡掉）。

发现每次把整个栈转移过去有点极端了。事实上，每次只转移栈底的 \(\frac{siz}2\) 个物品即可均摊 \(\mathcal O(1)\)，这是一种在国外普及度很高的神秘科技。大概证明是，把底部 \(\frac{siz}2\) 个物品和顶部 \(\frac{siz}2\) 个物品一一配对，形成一种关系 \((u,v)\)，后续只有在 \(u\) 或 \(v\) 出队时，另一个才可能继续发生栈间的转移。于是总的转移物品个数与入队次数 \(+\) 出队次数相当，整体复杂度 \(\mathcal O(qV)\)。

另外一开始把 \(f_i\) 定义成了体积恰好为 \(i\) 导致查询变成 \(\Theta(V^2)\)。。联考前得复习下普及组算法，真不知道自己能这么唐。

#include <cstdio>
#include <vector>
#include <stack>
#include <cstring>using namespace std;void cmx(int &x,int y){if(x<y) x=y;}const int W=2327;int rbq[W];struct BMI{int p,t;};void ad(int* f,BMI x){for(int i=W-1;i>=x.p;--i) cmx(f[i],f[i-x.p]+x.t);
}namespace DS{class st{struct node{BMI x;int f[W];}tmp;public:stack<node> s;bool emp(){return s.empty();}void push(BMI x){memcpy(tmp.f,s.empty()?rbq:s.top().f,W<<2);ad(tmp.f,x);tmp.x=x;s.push(tmp);}BMI acs_tp(){BMI x=s.top().x;s.pop();return x;}}l,r,t;void adj(){bool flg=r.emp();if(flg) l.s.swap(r.s);int s=(int)r.s.size()>>1;while(s--) t.push(r.acs_tp());while(!r.emp()) l.push(r.acs_tp());while(!t.emp()) r.push(t.acs_tp());if(flg) l.s.swap(r.s);}int qry(int p){int *f=l.emp()?rbq:l.s.top().f,*g=r.emp()?rbq:r.s.top().f,res=0;for(int i=0;i<=p;++i) cmx(res,f[i]+g[p-i]);return res;}BMI acs_frt(){if(l.emp()) adj();return l.acs_tp();}void pop_bck(){if(r.emp()) adj();r.acs_tp();}
}const int N=34102;vector<int> vc[N];struct qry{int p,i;};
vector<qry> qr[N];bool del[N],ref[N];BMI w[N];int ans[N];void dfs(int u){if(del[u]) w[u]=DS::acs_frt();if(ref[u]) DS::r.push(w[u]);for(auto[p,i]:qr[u]) ans[i]=DS::qry(p);for(int v:vc[u]) dfs(v);if(ref[u]) DS::pop_bck();if(del[u]) DS::l.push(w[u]);
}int cur[N],v;int main()
{int q,V=1,qc=0;scanf("%d",&q);while(q--){int f,x;scanf("%d%d",&f,&x);switch(f){case 1:vc[cur[x]].push_back(cur[++V]=++v);break;case 2:vc[cur[x]].push_back(++v),ref[cur[x]=v]=1,scanf("%d%d",&w[v].p,&w[v].t);break;case 3:vc[cur[x]].push_back(++v),del[cur[x]=v]=1;break;case 4:int p;scanf("%d",&p);qr[cur[x]].push_back((qry){p,++qc});break;}}dfs(0);for(int i=1;i<=qc;++i) printf("%d\n",ans[i]);
}