11. Dual Diffusion Implicit Bridges for Image-to-Image Translation
该文提出一种双扩散隐式桥(Dual Diffusion Implicit Bridges, DDIBs)方法用于图像转换,其最大的特点在于处理源域图像的模型和处理目标域图像的模型是彼此分开独立的。使用源域图像训练一个扩散模型 v θ ( s ) v^{(s)}_{\theta} vθ(s),然后使用目标域图像训练另外一个模型 v θ ( t ) v^{(t)}_{\theta} vθ(t),给定一个源域图像 x ( s ) x^{(s)} x(s),首先利用 v θ ( s ) v^{(s)}_{\theta} vθ(s)将其转化为潜在特征 x ( l ) x^{(l)} x(l),然后再经过 v θ ( t ) v^{(t)}_{\theta} vθ(t)将其转化为目标域图像 x ( t ) x^{(t)} x(t)。这带来一个好处,训练过程中不需要同时使用源域和目标域图像对模型进行训练,这在一些对数据私密性要求较高的领域是十分必要的。此外,源域和目标域模型是可以相互转换的,即源域扩散模型,反过来也可以当作目标域的生成模型使用,这就能够实现从目标域向源域的转换。而且一个训练好的扩散模型可以跟任意的目标域生成模型结合,这就使得许多图像转换任务所需模型的数量是随着域的数量线性增长,而不是原本的二次方增长。还有一个重大优势,就是这个方法采用了DDIM模型中的常微分方程ODE建模方式,这就在理论上保证了转化过程具有非常好的循环一致性,即由源域图像 x ( s ) x^{(s)} x(s),生成的目标域图像 x ( t ) x^{(t)} x(t),再经过反向生成得到的伪源域图像 x ′ ( s ) x'^{(s)} x′(s)与初始的源域图像 x ( s ) x^{(s)} x(s)之间仅存在一个微小的ODE求解过程中的离散化误差。最后,就是这个方法其实对于扩散模型和生成模型 v θ v_{\theta} vθ是没有什么限制的,我们可以使用各种最新的模型来进行扩散和生成。
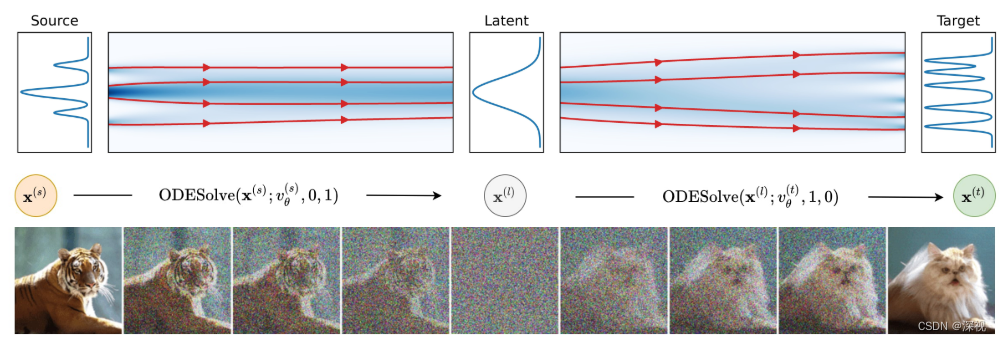
作者首先对基于分数的生成模型(SGMs)进行了回顾,提到其中的两个重要代表作SMLD(NCSN)和DDPM算法都是可以用随机微分方程SDEs来描述的,其扩散和生成过程如下 d x = f ( x , t ) d t + g ( t ) d w , d x = [ f − g 2 ∇ x log p t ( x ) ] d t + g ( t ) d w (1) \mathrm{d} \mathbf{x}=\mathbf{f}(\mathbf{x}, t) \mathrm{d} t+g(t) \mathrm{d} \mathbf{w}, \quad \mathrm{d} \mathbf{x}=\left[\mathbf{f}-g^{2} \nabla_{\mathbf{x}} \log p_{t}(\mathbf{x})\right] \mathrm{d} t+g(t) \mathrm{d} \mathbf{w}\tag{1} dx=f(x,t)dt+g(t)dw,dx=[f−g2∇xlogpt(x)]dt+g(t)dw(1)同时,也提到任何的扩散过程都可以通过确定性的常微分方程来表示,称之为概率流常微分方程(PF ODEs),其扩散过程表示如下 d x = [ f ( x , t ) − 1 2 g ( t ) 2 ∇ x log p t ( x ) ] d t (2) \mathrm{d} \mathbf{x}=\left[\mathbf{f}(\mathbf{x}, t)-\frac{1}{2} g(t)^{2} \nabla_{\mathbf{x}} \log p_{t}(\mathbf{x})\right] \mathrm{d} t\tag{2} dx=[f(x,t)−21g(t)2∇xlogpt(x)]dt(2)如果我们用 v θ = d x / d t v_{\theta}=\mathrm{d} \mathbf{x}/\mathrm{d} t vθ=dx/dt来表示参数为 θ \theta θ的一个速度场(velocity field),也就是公式(2)中方括号里的内容,则使用ODE求解由 x ( t 0 ) x(t_0) x(t0)到 x ( t 1 ) x(t_1) x(t1)的映射关系过程表示如下 ODESolve ( x ( t 0 ) ; v θ , t 0 , t 1 ) = x ( t 0 ) + ∫ t 0 t 1 v θ ( t , x ( t ) ) d t (3) \operatorname{ODESolve}\left(\mathbf{x}\left(t_{0}\right) ; v_{\theta}, t_{0}, t_{1}\right)=\mathbf{x}\left(t_{0}\right)+\int_{t_{0}}^{t_{1}} v_{\theta}(t, \mathbf{x}(t)) \mathrm{d} t\tag{3} ODESolve(x(t0);vθ,t0,t1)=x(t0)+∫t0t1vθ(t,x(t))dt(3)当 t 0 = 0 , t 1 = 1 t_0=0,t_1=1 t0=0,t1=1时就表示扩散过程,而当 t 0 = 1 , t 1 = 0 t_0=1,t_1=0 t0=1,t1=0时就表示生成过程,DDIBs的扩散和生成流程如下图所示,其中求解器ODESolve本文使用的是DDIM,当然其他的求解器也是可以的。此外 v θ v_{\theta} vθ中的未知量 ∇ x log p t ( x ) \nabla_{\mathbf{x}} \log p_{t}(\mathbf{x}) ∇xlogpt(x)通常用一个噪声估计网络或者叫做分数估计网络 s θ s_{\theta} sθ来进行估计, s θ s_{\theta} sθ可采用带有注意力机制的UNet模型或者条件UNet模型。

其实讲到这里,DDIBs方法的过程和特点就已经介绍完了,下面作者又分析了其背后的理论依据,作者是从薛定谔桥问题(Schrodinger Bridges Problem,SBP)的角度来描述DDIBs的理论基础的。假设 Ω = C ( [ 0 , 1 ] ; R n ) \Omega=C\left([0,1];\mathbb{R}^{n}\right) Ω=C([0,1];Rn)是在时间[0,1]范围内 n n n维实值连续函数的路径空间, D ( p 0 , p 1 ) \mathcal{D}\left(p_{0}, p_{1}\right) D(p0,p1)是空间 Ω \Omega Ω上所有的分布集合,其在时刻 t = 0 , t = 1 t=0,t=1 t=0,t=1上的边缘分布分别为 p 0 , p 1 p_0,p_1 p0,p1。给定一个先验的参考度量 W W W,则SBP就是要寻找在 p 0 p_0 p0和 p 1 p_1 p1之间随时间 t t t变化的概率最大的进化路径,也就是说从 D ( p 0 , p 1 ) \mathcal{D}\left(p_{0}, p_{1}\right) D(p0,p1)寻找一个分布使得其与参考度量 W W W之间的KL散度最小,即下式所示 P S B P : = arg min { D K L ( P ∥ W ) ∣ P ∈ D ( p 0 , p 1 ) } (4) P_{S B P}:=\arg \min \left\{D_{K L}(P \| W) \mid P \in \mathcal{D}\left(p_{0}, p_{1}\right)\right\}\tag{4} PSBP:=argmin{DKL(P∥W)∣P∈D(p0,p1)}(4)作者还解释到SBP实际上是一个带有额外熵正则项的Monge-Kantorovich (MK)最优传输问题(OT)。上面这一大段,其实我也没怎么看懂,大概的意思是SBP就是寻找一个时间跨度为 t t t,边缘分布分别为 p 0 p_0 p0和 p 1 p_1 p1的概率分布 P P P。那么SBP与上面提到的SGMs又有什么关系呢?作者引用他人研究的结果证明SGMs是一种隐式的最优传输模型,对应着带有线性或退化漂移(linear or degenerate drifts)的SBP。简单理解为SGMs是退化版的SBP,是SBP的一个特例。那么用SBP来描述扩散和生成过程如下: d x = [ f + g 2 ∇ x log Φ t ( x ) ] d t + g ( t ) d w , d x = [ f − g 2 ∇ x log Φ ^ t ( x ) ] d t + g ( t ) d w (5) \mathrm{d} \mathbf{x}=\left[\mathbf{f}+g^{2} \nabla_{\mathbf{x}} \log \Phi_{t}(\mathbf{x})\right] \mathrm{d} t+g(t) \mathrm{d} \mathbf{w}, \quad \mathrm{d} \mathbf{x}=\left[\mathbf{f}-g^{2} \nabla_{\mathbf{x}} \log \hat{\Phi}_{t}(\mathbf{x})\right] \mathrm{d} t+g(t) \mathrm{d} \mathbf{w}\tag{5} dx=[f+g2∇xlogΦt(x)]dt+g(t)dw,dx=[f−g2∇xlogΦ^t(x)]dt+g(t)dw(5)其中 Φ t , Φ ^ t {\Phi}_{t},\hat{\Phi}_{t} Φt,Φ^t为薛定谔因子,其满足 p t ( x ) = Φ t ( x ) Φ ^ t ( x ) p_{t}(\mathbf{x})=\Phi_{t}(\mathbf{x}) \hat{\Phi}_{t}(\mathbf{x}) pt(x)=Φt(x)Φ^t(x)。式中 z t = g ( t ) ∇ x log Φ t ( x ) \mathbf{z}_{t}=g(t) \nabla_{\mathbf{x}} \log \Phi_{t}(\mathbf{x}) zt=g(t)∇xlogΦt(x)和 z ^ t = g ( t ) ∇ x log Φ ^ t ( x ) \hat{\mathbf{z}}_{t}=g(t) \nabla_{\mathbf{x}} \log \hat{\Phi}_{t}(\mathbf{x}) z^t=g(t)∇xlogΦ^t(x)能够充分的表征SBP的动态变化过程,因此可以被看作是扩散和生成过程所遵循的策略。从对数似然的角度来看,当 z t , z ^ t \mathbf{z}_{t}, \hat{\mathbf{z}}_{t} zt,z^t满足以下条件时,SBP和SGMs是等价的 ( z t , z ^ t ) = ( 0 , g ( t ) ∇ x log p t ( x ) ) (6) \left(\mathbf{z}_{t}, \hat{\mathbf{z}}_{t}\right)=\left(0, g(t) \nabla_{\mathbf{x}} \log p_{t}(\mathbf{x})\right)\tag{6} (zt,z^t)=(0,g(t)∇xlogpt(x))(6)当然与SGMs相似,SBP也能够推导出其对应的确定性概率流常微分方程PE ODE,如下所示 d x = [ f ( x , t ) + g ( t ) z − 1 2 g ( t ) ( z + z ^ ) ] d t \mathrm{d} \mathbf{x}=\left[\mathbf{f}(\mathbf{x}, t)+g(t) \mathbf{z}-\frac{1}{2} g(t)(\mathbf{z}+\hat{\mathbf{z}})\right] \mathrm{d} t dx=[f(x,t)+g(t)z−21g(t)(z+z^)]dt其中 z \mathbf{z} z只与 x \mathbf{x} x有关,与时间 t t t无关。
费了这么多力气,作者就想说明一点DDIBs是两个级联的薛定谔桥,分别连接了源域和潜在空间以及潜在空间和目标域。这就是该文提出方法名字的来源,双扩散隐式桥(Dual Diffusion Implicit Bridges, DDIBs)是基于去噪扩散隐式模型(Denoising Diffusion Implicit Models, DDIM)的且包含两个独立的薛定谔桥以连接数据和潜在空间分布。后面作者在一个2维图像数据集上,验证了DDIBs方法所具备的图像转换的平滑性和循环一致性,如下图所示
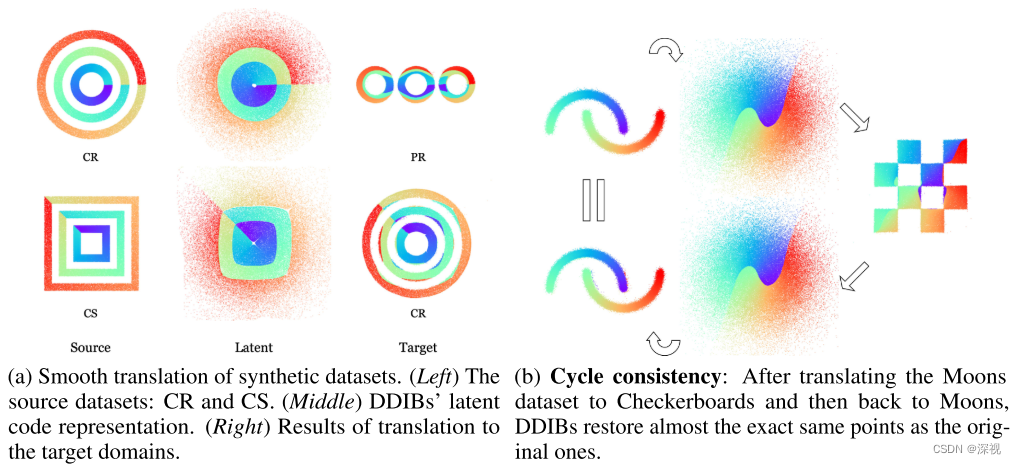
由图a可以看出来,当图像从一种形状转换到另一种形状时,其颜色的分布情况几乎与源图像保持一致;由图b可以看出,当图像从形状A转换到B再转换回A时,两者之间几乎没有任何差别,这就显著表明了生成过程具备很好的循环一致性。
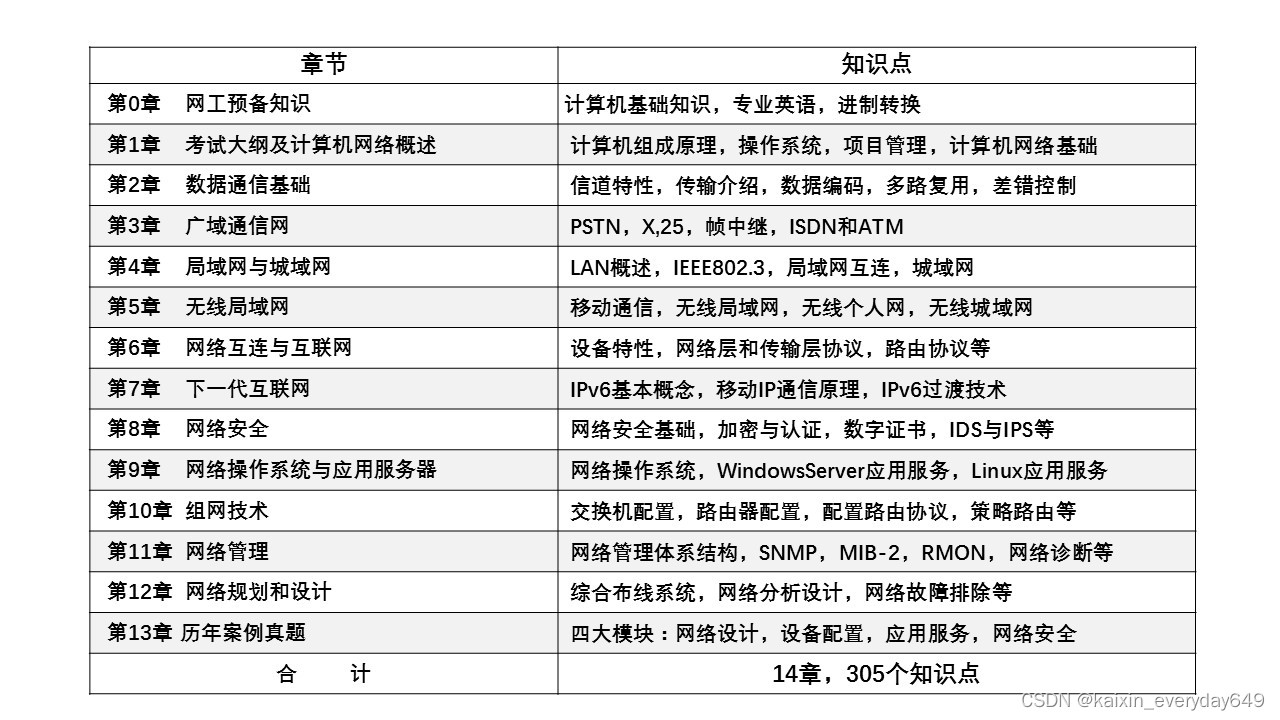
此外,作者还利用条件扩散模型测试了DDIBs由一个源域转换到多个目标域的表现,如下图所示

可以看到,当源域图像(狮子,类别代号291)转化为其他多个类别时,再保留原有的吼叫姿态的同时,又能很好的兼顾目标类别的特征。




![[ESP32]:基于HTTP实现百度AI识图](https://img-blog.csdnimg.cn/direct/72bed8619792476ab2cfebf1175d5222.png#pic_center)