🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~
✨主攻领域:【渗透领域】【应急响应】 【Java、PHP】 【VulnHub靶场复现】【面试分析】
🎉点赞➕评论➕收藏 == 养成习惯(一键三连)😋
🎉欢迎关注💗一起学习👍一起讨论⭐️一起进步📝文末有彩蛋
🙏作者水平有限,欢迎各位大佬指点,相互学习进步!目录
数组的相关函数
编程思想
递推算法
递归算法
数组的相关函数
1)排序函数:对数组元素进行排序,都是按照ASCII码进行比较,可以进行英文比较
sort():顺序排序(下标重排)
rsort():逆序排序
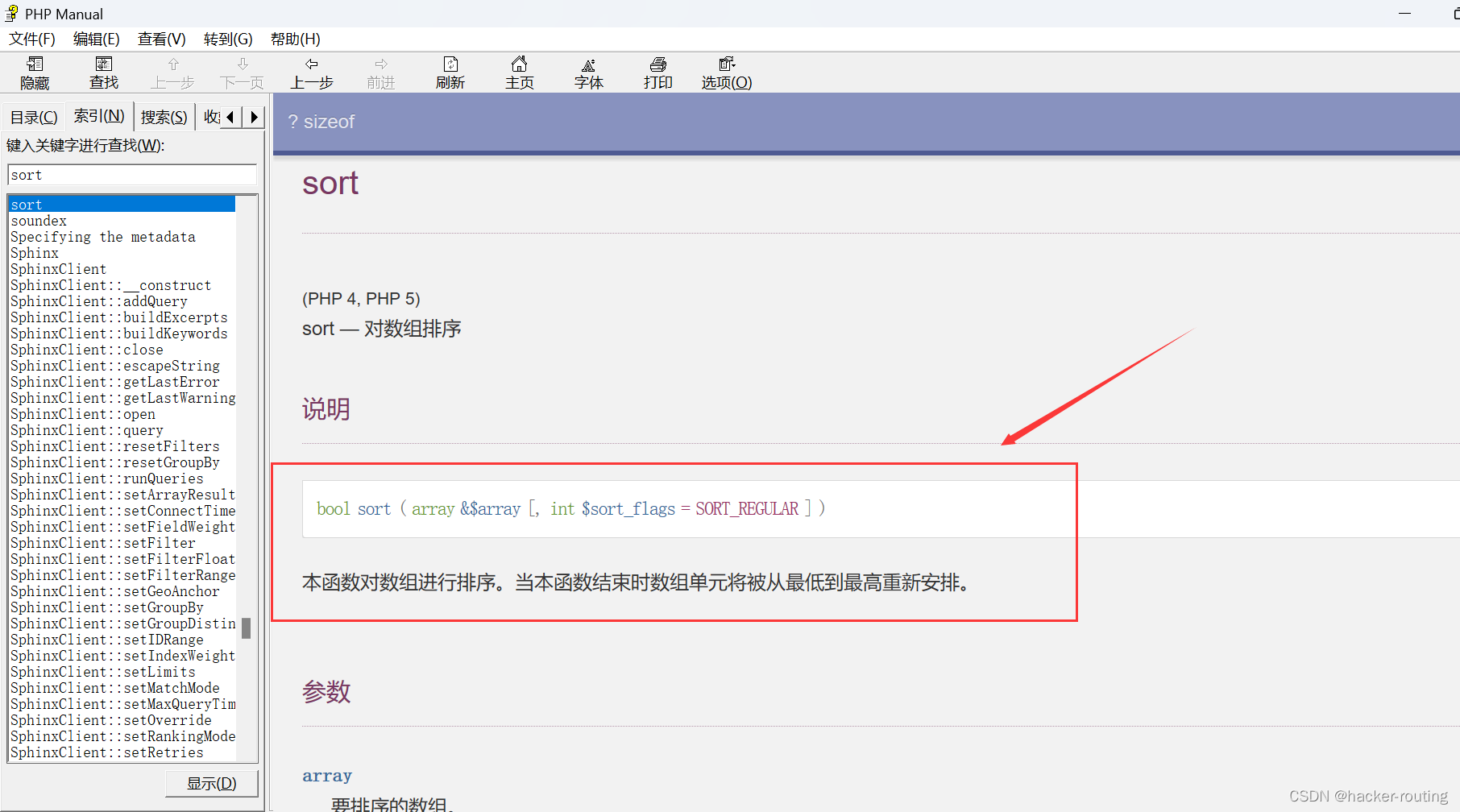

asort():顺序排序(下标保留)
arsort():逆序排序
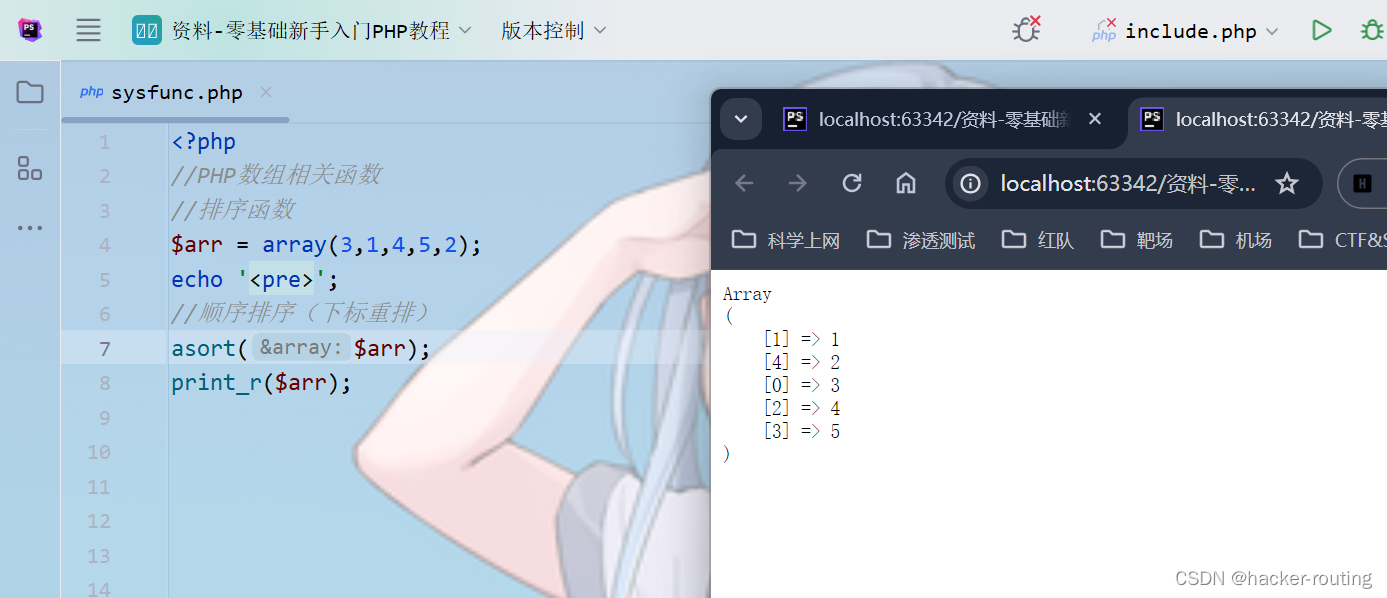
ksort():顺序排序:按照键名(下标)
krsort():逆序排序
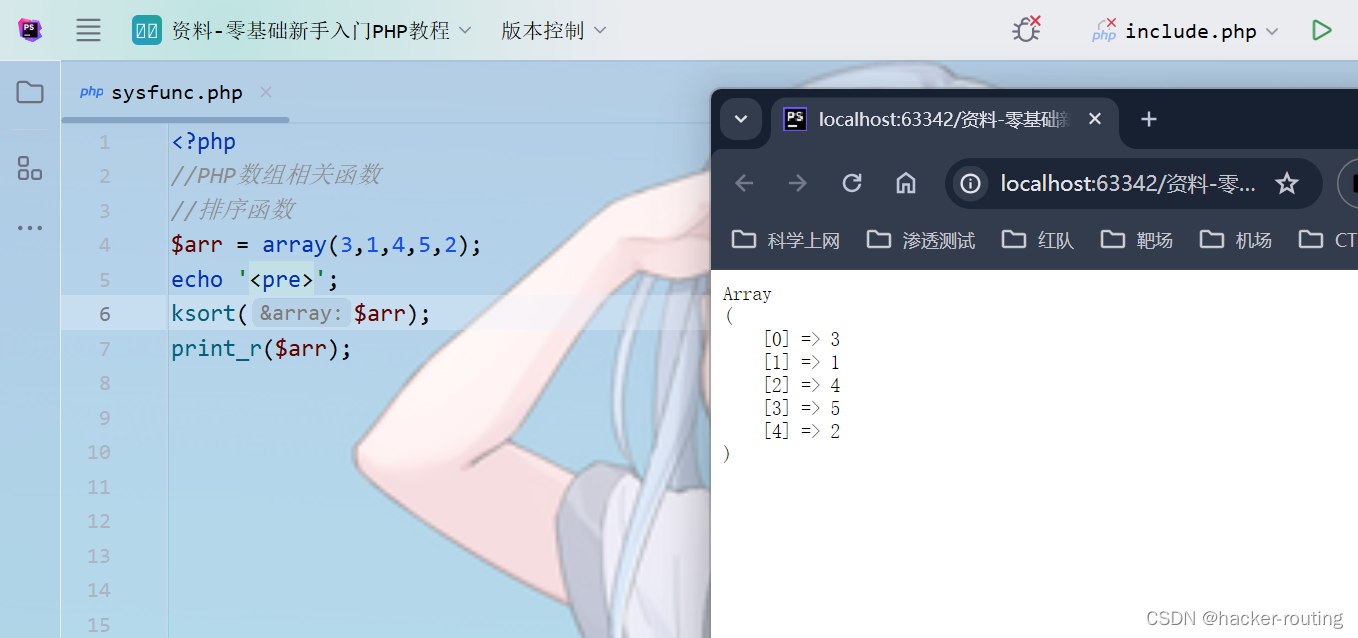
shuffle():随机打乱数组元素,数组下标会重排
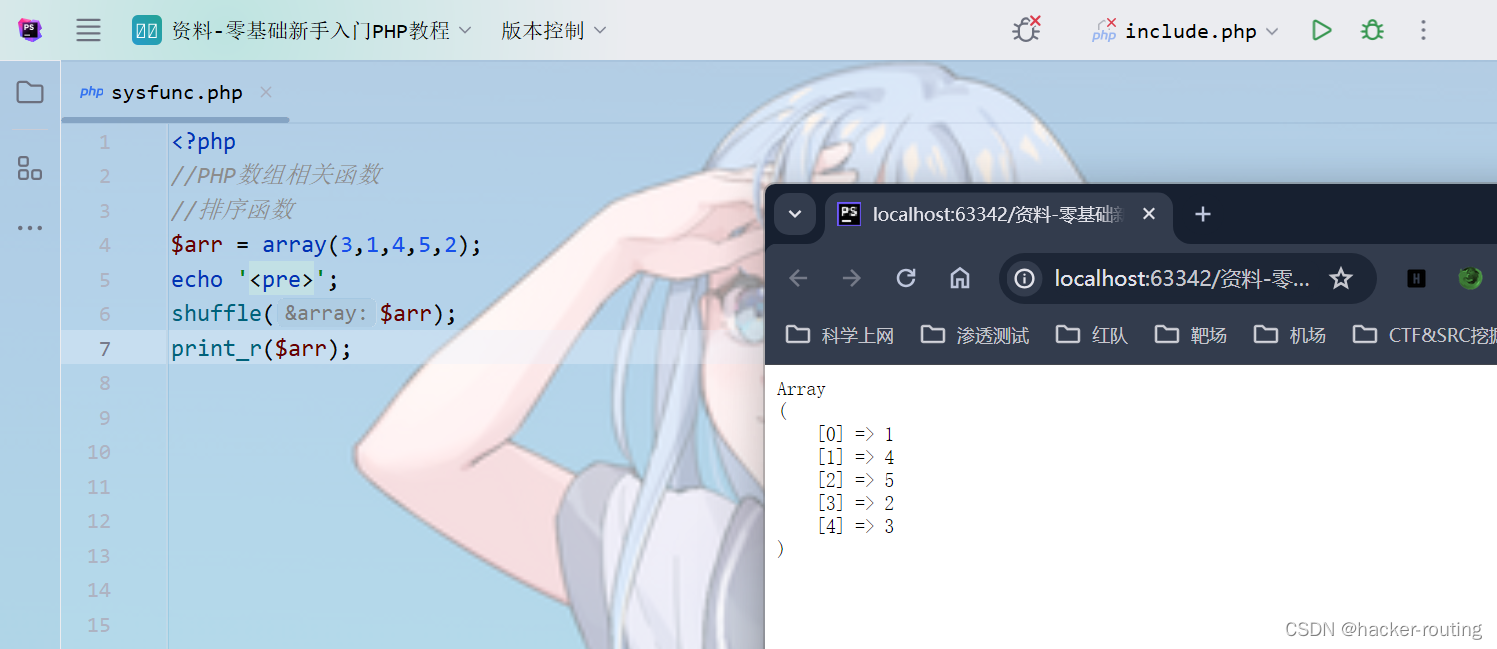
2)指针函数
reset():重置指针,将数组指针回到首位
end():重置指针,将数组指针指导最后一个元素
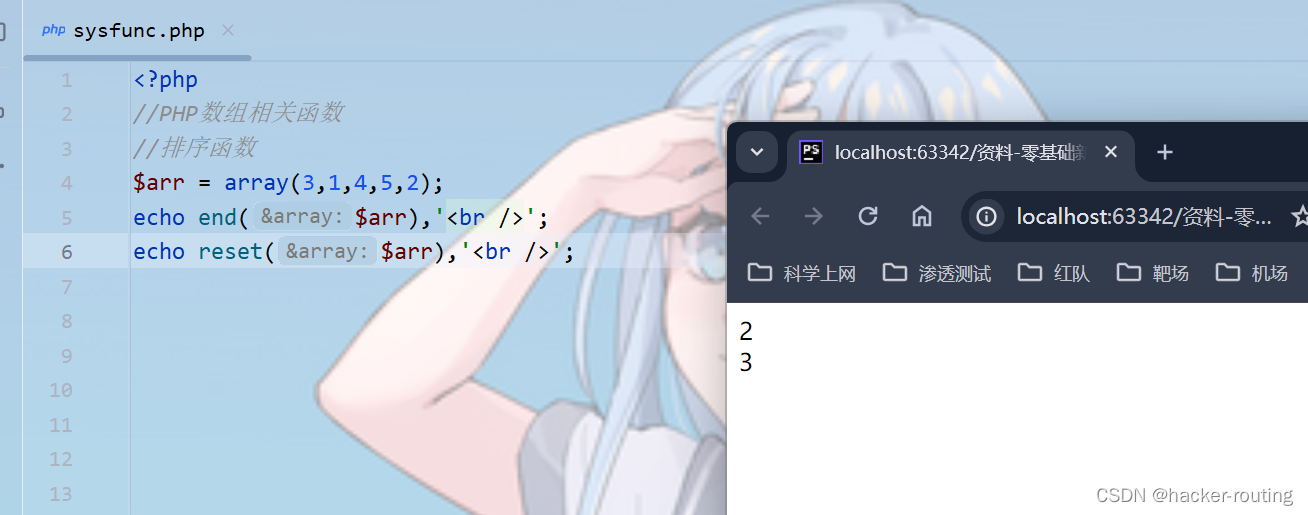
next():指针下移,取得下一个元素的值
prev():指针上移,取得上一个元素的值

注意事项:next和prev会移动指针,有可能导致指针移动到最前或者最后(离开数组),导致数组不能使用,通过next和prev不能回到真确的指针位置。只能通过end或者reset进行指针重置
3)其他函数
count():统计数组中元素的数量
array_push():往数组中加入一个元素(数组后面)
array_pop():从数组中取出一个元素(数组后面)
array_shift():从数组中取出一个元素(数组前面)
array_unshift():从数组中加入一个元素(数组前面)
PHP模拟数据结构:
栈:压栈,先进去后出来(FILO)

编程思想
编程思想:如何利用数学模式,来解决对应的需求问题;然后利用代码实现对应的数据模型(逻辑)。
算法:使用代码实现对应的数学模型,从而解决对应的业务问题。
递推算法
递推算法是一种简单的算法,即通过已知条件,利用特定关系得出中间推论,直至得到结果的算法。递推算法分为顺推和逆推两种。
顺推:通过最简单的条件(已知),然后逐步推演结果
逆推:通过结果找到规律,然后推到已知条件
斐波那契数列:1 1 2 3 5 8 13 …,通常需求:请求得指定位置N所对应的值是多少
找规律:
1、 第一个数是1
2、 第二个数也是1
3、 从第三位开始:属于前两个数的和
代码解决思路:
1、 如果数字位置为1和2,结果都是1
2、 从第三个开始,想办法得到前两个的结果,就可以得到
终极解决办法:想办法把要求的位置之前的所有的值都列出来,那么要求的数就可以通过前两个之和计算出来:使用数组存储所有结果即可。
递推算法求斐波那契数列:
<?php
//递推思想(算法)
//已知条件:第一个和第三个数都是1,第三个开始为前两个之和
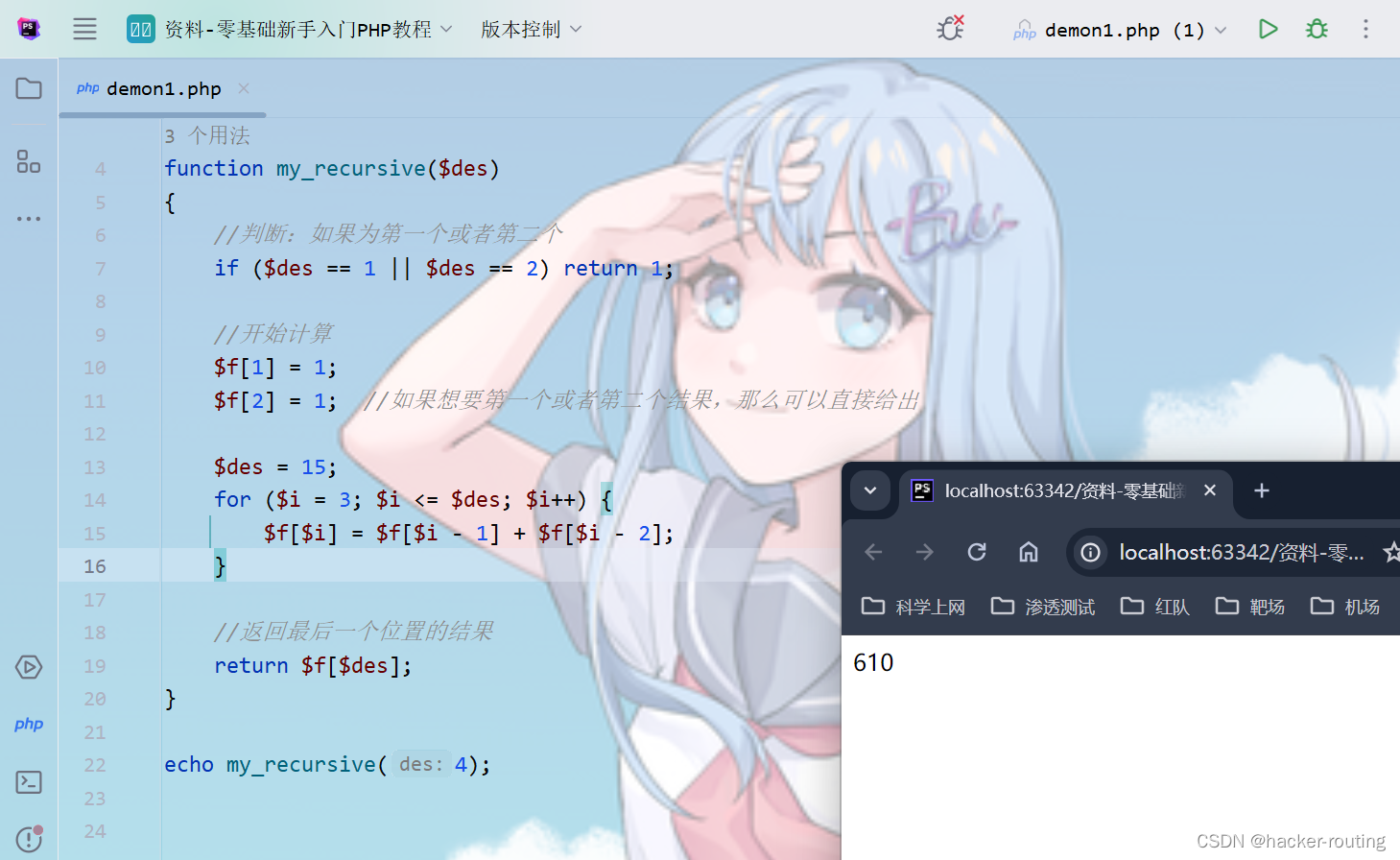
function my_recursive($des)
{//判断:如果为第一个或者第二个if ($des == 1 || $des == 2) return 1;//开始计算$f[1] = 1;$f[2] = 1; //如果想要第一个或者第二个结果,那么可以直接给出$des = 15;for ($i = 3; $i <= $des; $i++) {$f[$i] = $f[$i - 1] + $f[$i - 2];}//返回最后一个位置的结果return $f[$des];
}echo my_recursive(4);递归算法
递归算法是把问题转化为规模缩小了的同类问题的子问题。然后递归调用函数(或过程)来表示问题的解。
1、 简化问题:找到最优子问题(不能再小)
2、 函数自己调用自己
斐波那契数列:1 1 2 3 5 8 13 …
需求:求指定位置的数列的值
规律:第一个和第二个为1,从第三个开始为前两个之后
F(N) = F(N-1) + F(N-2);
F(N-1) = F(N-2) + F(N - 3);
…
F(2) = F(1) = 1;
递归思想中:有两个非常重要的点
递归点:发现当前问题可以有解决当期问题的函数,去解决规模比当前小一点的问题来解决
F(N) = F(N - 1) + F(N - 2);
递归出口:当问题解决的时候,已经到达(必须有)最优子问题,不能再次调用函数
如果一个函数递归调用自己而没有递归出口:就是死循环
递归的本质是函数调用函数:一个函数需要开辟一块内存空间,递归会出现同时调用N多个函数(自己):递归的本质是利用空间换时间
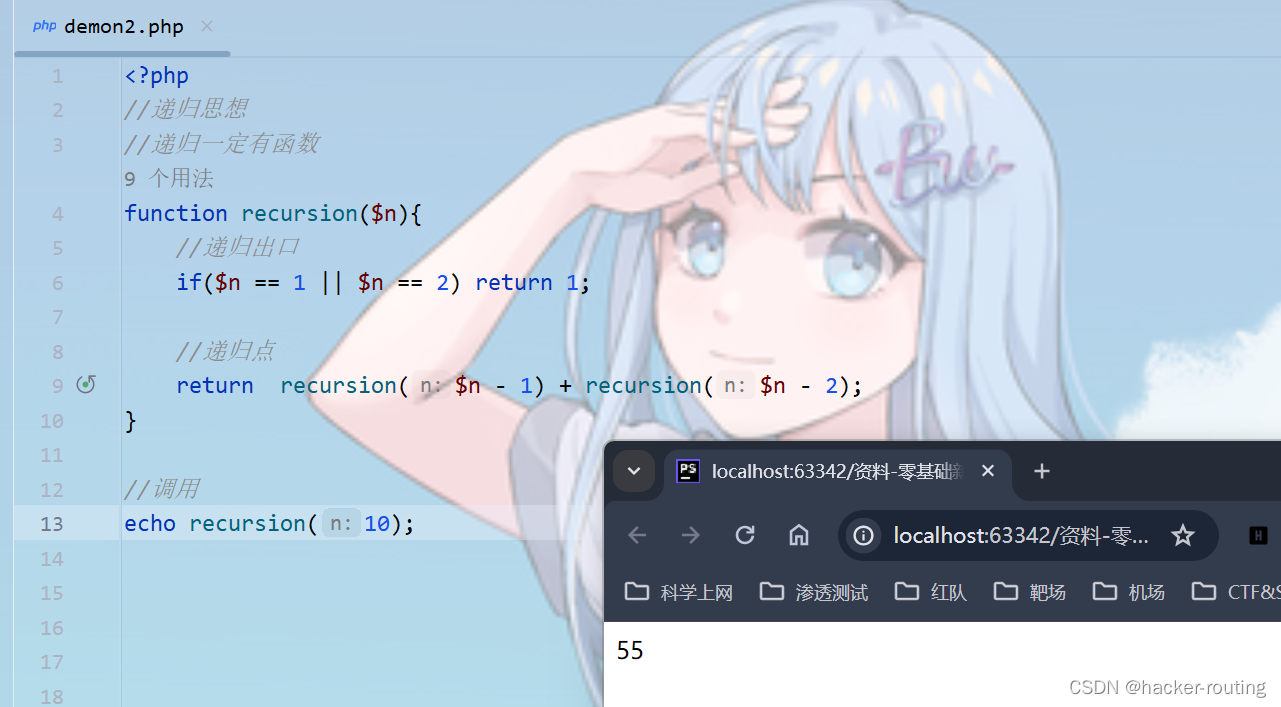
<?php
//递归思想
//递归一定有函数
function recursion($n){//递归出口if($n == 1 || $n == 2) return 1;//递归点return recursion($n - 1) + recursion($n - 2);
}//调用
echo recursion(10);