评价:
高情商:收获很大 ,让自己进一步认清自己。
低情商:题目难,自己太菜了。
今天还有一些其他事,剩下的题明天再补。
我们从a题开始吧:
A.签到

我们只要看看其中的max与min是否不符合即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,a[1000100],b[1000100],maxx=-1e8,minn=1e8;
int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++){maxx=max(maxx,a[i]);minn=min(minn,a[i]);}if(minn-1<1&&maxx+1>m) cout<<"No";else cout<<"Yes";
}B.贪心(喵喵喵)
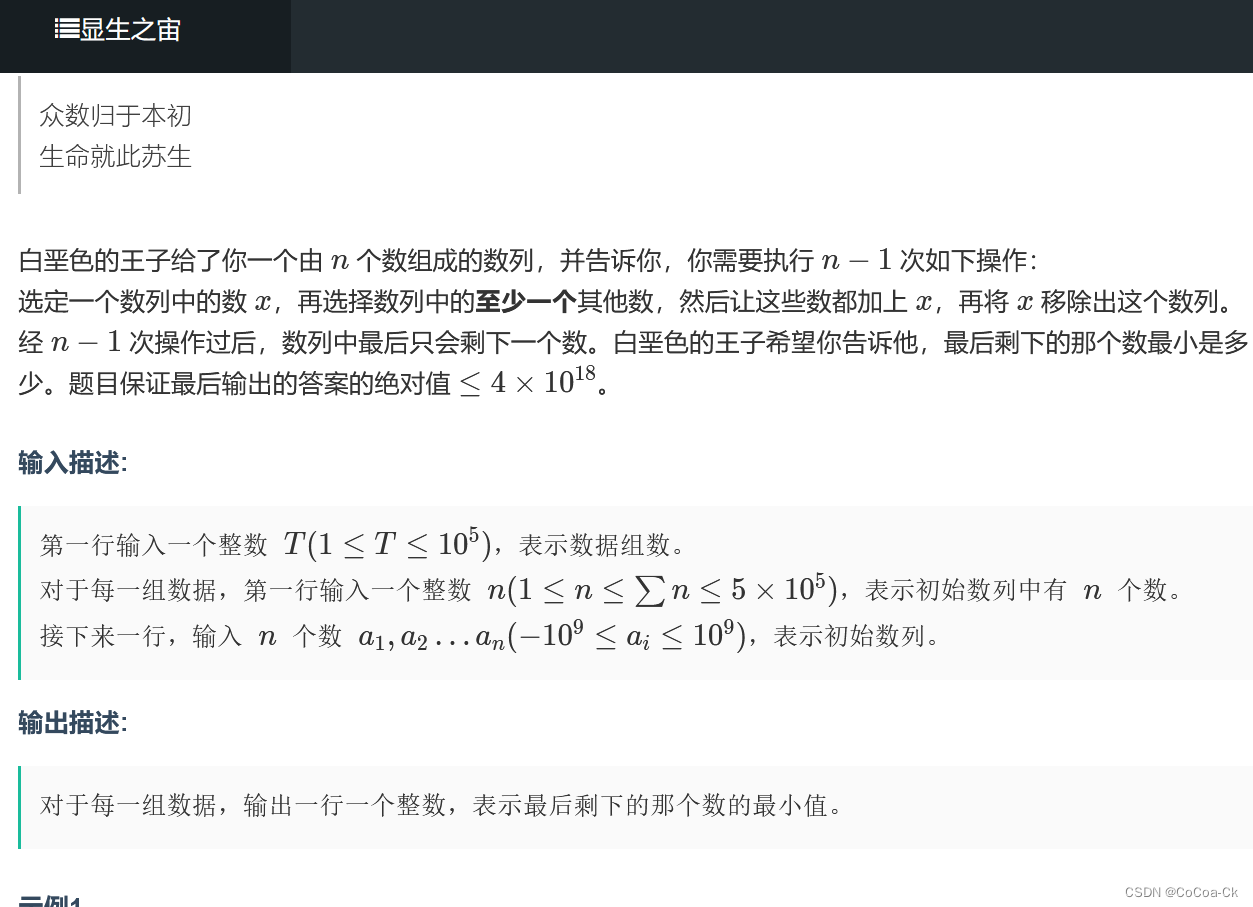
首先我们可以确定一个结论:
对于负数,我们把全部值都加它,对于正数,我们只要让他加给答案即可。
显然最后留下的一定是原来最大的(粗糙的想一想,每一个数都对答案至少,并且假如一个值一开始1,后来变成负数,我们也把全部值都加它。
这样如果直接模拟n^2,于是我们用sum表示全局要加的值,ans为只有答案要加的,这样子就是n的复杂度了,还是比较妙的。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
long long t,n,a[500010];
bool cmp(int a,int b){return a<b;
}
int main(){cin>>t;while(t--){cin>>n;for(int i=1;i<=n;i++) scanf("%lld",&a[i]);sort(a+1,a+n+1,cmp);long long sum=0,ans=0;for(int i=1;i<=n-1;i++){long long ck=sum+a[i];if(ck>=0) ans+=ck;else{sum+=ck;}}printf("%lld\n",a[n]+sum+ans);}
}C.思维+连通块
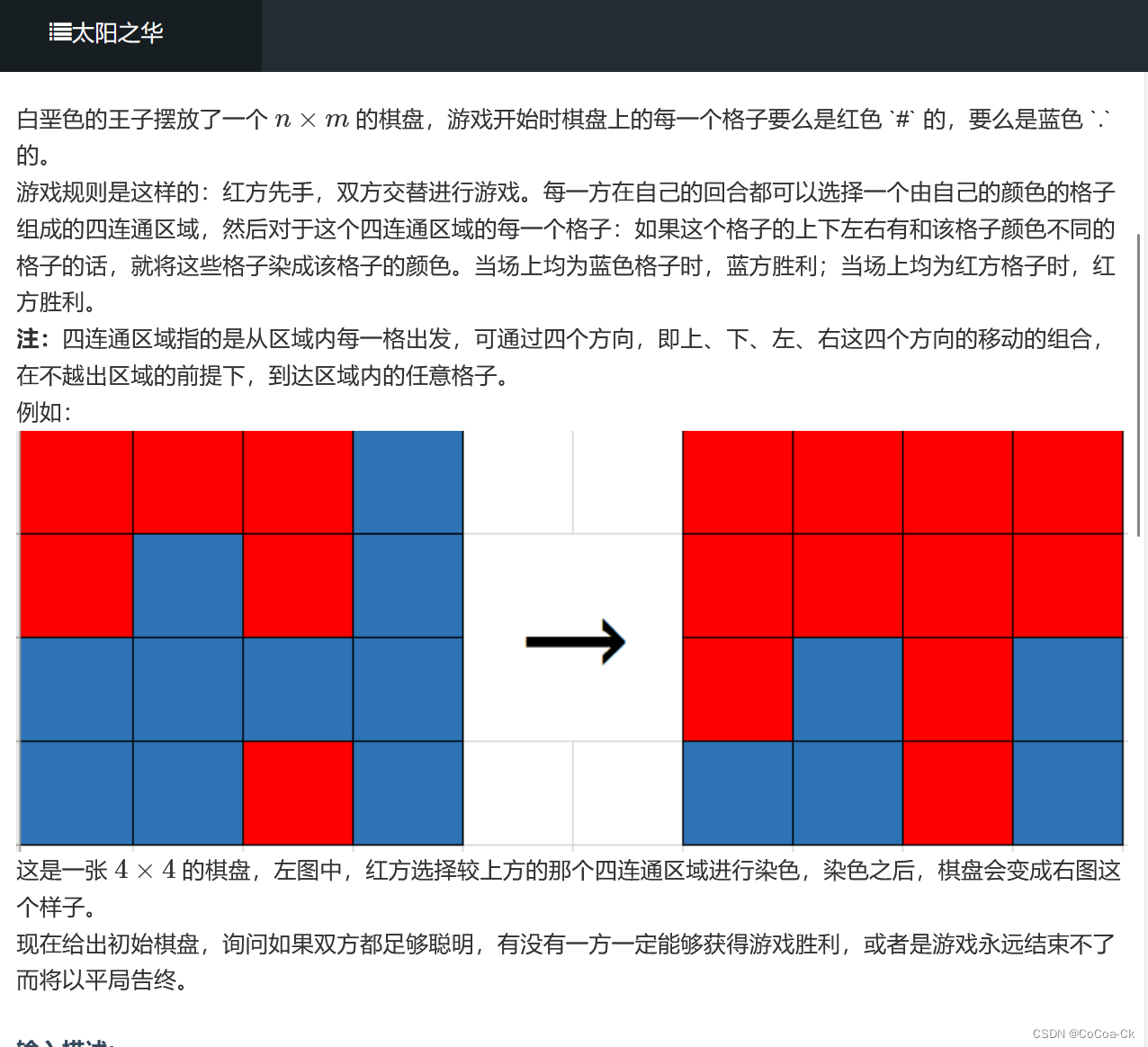
首先,若第一次红可以吃掉蓝,则红胜,否则,蓝一定存在一块,以他扩展,则中心那一个一定不会被吃,因此蓝一定不会输,同理红也一定不会输,那么就是平局。
因此我们可以得到:若开始时红的一个联通块不能吃掉蓝的全部格子就是平局,反之红赢。
这里我们用DFS,并用set记录可以删的数(顺便去重),考虑到x<2000,我们可以在加时直接在x上*2020,这样形成的数是唯一的。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int t,n,m,blue,dir[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
char a[2010][2010],x;
bool vis[2010][2010];
set<int> s;
void dfs(int x,int y){if(vis[x][y]) return;vis[x][y]=1;for(int i=0;i<4;i++){int xx=x+dir[i][0];int yy=y+dir[i][1];if(xx<1||xx>n||yy<1||yy>m) continue;if(a[xx][yy]=='#') dfs(xx,yy);else s.insert(xx*2020+yy);}
}
int main(){cin>>t;while(t--){blue=0;int win=0;memset(vis,0,sizeof(vis));cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf(" %c",&x);a[i][j]=x;if(x=='.') blue++;}}if(blue==n*m){cout<<"Blue"<<endl;continue;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(vis[i][j]) continue;if(a[i][j]=='#'){s.clear();dfs(i,j);if(s.size()==blue) win=1;}}}if(win) cout<<"Red"<<endl;else cout<<"Draw"<<endl;}
}D.BFS+DP

首先注意到每一个边都为1,显然是考虑BFS,而我们关心的是到x点的每一个距离有几个点。
我们不妨令dp[i][j]表示考虑了dis<=i的所有点放了j个喵点的方案数。
易得状态转移方程dp[i][k]=dp[i-1][k]+dp[i-1][k-1]*c[i](dis==i的个数)。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
long long n,m,q,x,u,v,k,dis[1000100],mod=1e9+7;
vector<int> edge[1000100];
long long dp[5001][5005],cnt[5050];
queue<int> qq;
int main(){cin>>n>>m>>q>>x;for(int i=1;i<=m;i++){scanf("%lld%lld",&u,&v);edge[u].push_back(v);edge[v].push_back(u);}memset(dis,0x3f,sizeof(dis));dis[x]=0;qq.push(x);while(!qq.empty()){int ck=qq.front();qq.pop();for(int i=0;i<edge[ck].size();i++){if(dis[edge[ck][i]]<=5000) continue;dis[edge[ck][i]]=dis[ck]+1;qq.push(edge[ck][i]);}}for(int i=1;i<=n;i++){cnt[dis[i]]++;}dp[0][0]=1;for(int i=1;i<=5000;i++){for(int j=0;j<=5000;j++){dp[i][j]=dp[i-1][j];if(j) dp[i][j]+=dp[i-1][j-1]*cnt[i]%mod;dp[i][j]=dp[i][j]%mod;}}for(int i=1;i<=q;i++){cin>>k;printf("%lld\n",dp[5000][k]);}
}