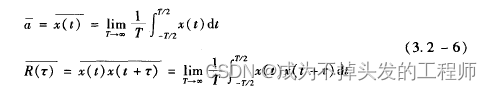HGNN+：通用超图神经网络-编程知识

文章信息

文章题为“HGNN+：General Hypergraph Neural Networks”，该文章于2023年发表于“IEEE Transcation on Pattern Analysis and Machine Intelligence”。该文章是其会议版本的延续，主要提出了一种通用的超图神经网络框架用于解决分类任务。

摘要

图神经网络近年来受到越来越多的关注。然而，现有的图神经网络框架都是基于简单的图来部署的，这限制了它们在实际中处理多模态/多类型数据的复杂数据关联的应用。最近提出了一些基于超图的方法来解决多模态/多类型数据关联的问题，这些方法直接连接由每个单个模态/类型构建的超图，这很难学习到每个模态/类型的自适应权值。本文扩展了原始会议版本的HGNN，并引入了一个通用的高阶多模态/多类型数据相关建模框架HGNN+，以学习基于单个超图的框架中的最优表示。该模型是通过桥接多模态/多类型数据和超边缘与超边缘组来实现的。具体而言，文章首先构建超边缘组来表示每个特定模态/类型中具有显式或隐式图结构的潜在高阶相关性；进一步，采用自适应超边缘群融合策略，将不同模态/类型的关联有效地融合到一个统一的超图中。然后，利用在空间域中执行的一种新的超图卷积方案来学习用于各种任务的通用数据表示。文章在几个流行的数据集上评估了这个框架，并将其与最新的最先进的方法进行了比较。综合评估表明，文章提出的HGNN+框架可以持续优于现有的方法，特别是在建模隐式数据相关性时。此外，文章还为提出的框架发布了一个名为THU-DeepHypergraph的工具箱，可用于各种应用，如数据分类、检索和推荐。

文章的主要贡献总结如下：

1. 文章系统地介绍了一个通用的超图神经网络框架HGNNþ，其中包括超边建模和超图卷积两个主要步骤。在超图建模中，文章从概念上引入了“超边组”(hyperedge group)，并进一步定义了四种生成超边缘群的方法。提出了一种自适应超边缘群融合策略，以最优生成超图，更好地利用各种关联的互补信息。

2. 文章将原有的卷积策略HGNNConv从空间域扩展为一般的两阶段超图卷积运算。它还定义了一个特定的变体(即HGNNConv+)，与HGNN中的超图卷积相比，它具有更高的可扩展性。

3. 文章通过对具有/不具有图结构的数据以及具有超图结构的数据进行大量实验，验证了所提方法的有效性。此外，还提供了详细的数学讨论，以便对超图结构和所提出的图有更深入的理解。

基础知识

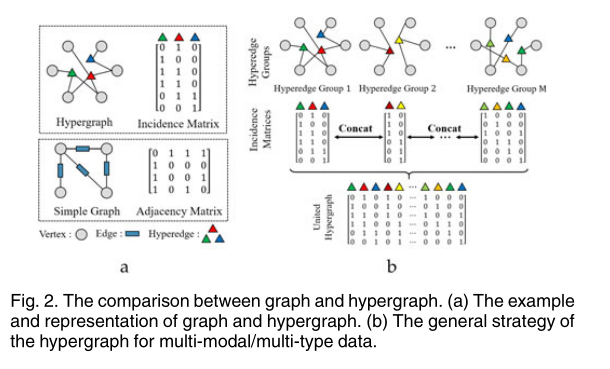
首先，超图是图的泛化。与图不同的是，超图中的边称为超边，它是超图中所有顶点的子集。如上图中的右侧图所示，一条超边可以连接多个顶点，是一系列顶点的集合。超图定义为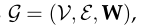，其中三元集中第一个集合表示顶点集，第二个表示边集，第三个表示权重矩阵。一个超图可以描述为一个关联矩阵H，其维度为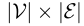，该关联矩阵的每一项定义为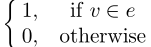。对于顶点v而言，其顶点的度定义为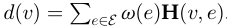，对于边e而言，其边的度定义为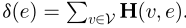。为进一步阐明文章的细节，下表展示了所有符号的定义。

问题定义：给定一个超图，分类任务转向对超图上的顶点进行分类，其中超图上的标签需要通过超图结构进行平滑处理。该任务可以表述如下：

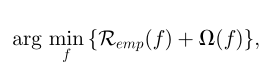
其中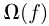，表示超图的正则化器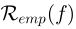，表示监督经验损失，f表示分类器。其中，正则化器表示如下：

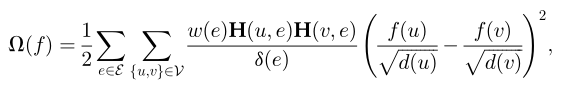
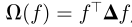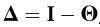通过简化，上式可表示为，其中和。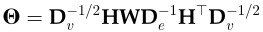

HGNN+框架

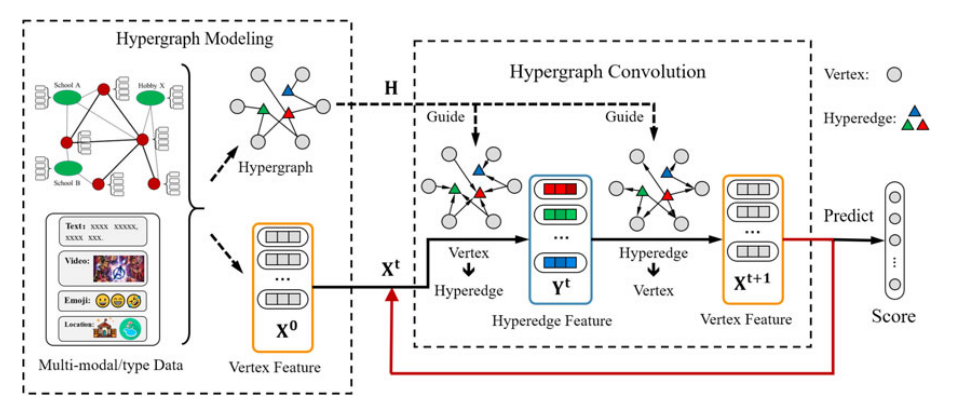
HGNN+的框架如上图所示，主要包含两个部分：超图建模和超图卷积。在超图建模的步骤中，将超图表示的关系用超图表示，将超图表示的关系用超图表示，将超图表示的关系用超图表示，将超图表示的关系用超图表示。有三种类型的超边缘群，分别在特征空间中使用成对边、k-Hop和邻居。在此过程中，将生成所有这些类型的超边组(如果可用)，并将它们连接到一个超图中，以便进行数据关联建模。在超图卷积步骤中，进行一组超图卷积族，即光谱超图卷积和空间超图卷积，用于表示学习。这些卷积过程可以利用来自高阶相关和多模态数据的信息来生成更好的表示。

1.超图建模：

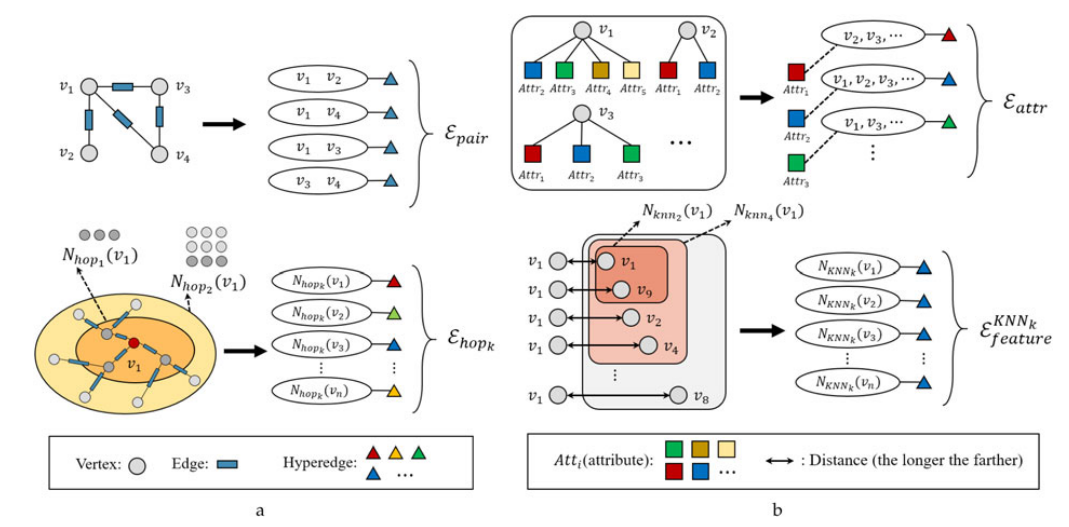
如上图所示文章首先系统地介绍了针对复杂应用的四种典型的超边缘群构建策略，包括基于图的表示、基于特征的表示和基于属性的表示；进一步，文章提出了一种自适应超边缘群融合策略，以平衡从不同方面构建的超边缘群的贡献。

在超图构建方面，当存在结构化数据时，设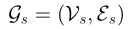表示图结构，A表示邻接矩阵，在这样的图结构下，可以生成如下两种类型的超边组：

使用成对边的超边组：该类超边目标是直接将图结构转化为一组2-均匀超边，如上图(a)的上半部分所示。其中，每条超边包括两个顶点，即在普通图中相邻接的两个顶点：

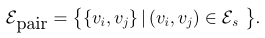
使用k-Hop邻居的超边组：该类超边旨在是通过图结构中的k距离可达的位置找到与中心点相关的所有顶点，如上图(a)下半部分所示。K距离可达的定义如下：

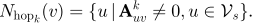
其中，k可以在区间[2,nv]中任选，nv表示图中的节点个数。k-Hop邻居的超边组定义如下：

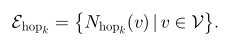
当不存在结构化数据时，一般存在两种类型的数据：类似属性的数据和每个顶点相关联的特征数据。基于上述两种数据类型，文章提出两种构建超边的方法。

使用属性构造超边组：给定类似属性的数据，例如不同主体共享的地理位置、时间和其他特定信息，可以使用属性空间中的邻居生成一组超边缘，如上图(b)上半部分所示，其中每个超边缘表示一个属性a(或该属性的一个子类型，如果存在)，并连接共享同一属性的所有主体。设A是一个集合，该集合包含所有属性或所有属性的子集，则超边组定义如下：

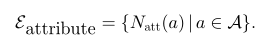
使用特征构建超边组：给定每个顶点的特征，第二种类型的超边可以通过在特征空间中查找每个顶点的邻居来生成。这里可以采用不同的策略。给定一个顶点作为质心，可以用超边缘将其在特征空间中的k近邻连接起来，或者选择与质心距离d内的所有邻居(包括质心)，如上图(b)下半部分所示。

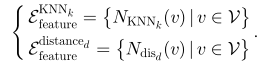
进一步，为融合上述特征，文章采用自适应融合的方式，即为不同的超边组分配不同的权重，其中权重为可学习参数。具体如下式表示：

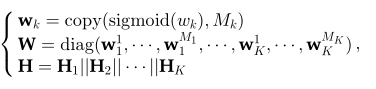
其中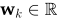，是可学习参数且一个超边组共享一个权值；是一个对角矩阵，表示超图对应超边的权重矩阵；是关联矩阵，该矩阵是所有超边组的拼接结果。针对多模型/多类型的数据，可以生成多个超边缘组。构造的超边群将生成超图关联矩阵和超边权矩阵，然后将其送入超图卷积层进行进一步计算。

2.超图卷积：

文章分别从光谱方面和空间方面定义了两个超图卷积HGNNConv和HGNNConv+。前者在作者的会议版论文中提出，后者则是作者在期刊版本中所提出的。对于超图上的空间卷积，文章首先定义了一个通用的空间超图卷积层，一个两阶段的消息传递框架。进一步，通过指定两个阶段的聚合函数，提出HGNNConv+。超图中的谱卷积本节不再介绍，主要针对空间超图卷积以及HGNNConv+进行介绍。

经过一些相关的定义和推导，可以得到通用的空间超图卷积层，其公式表达如下：

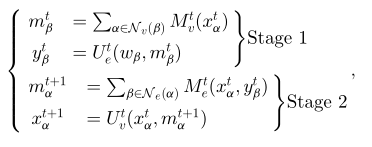
其中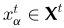，表示输入特征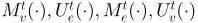，分别表示第t层的顶点信息函数、超边更新函数、超边信息函数和顶点更新函数，上述四个函数都可以依据需求定义。空间超图卷积层是利用超图结构中的高阶关系进行高级表示学习的。与图卷积中的单阶段信息传递相比，两阶段空间超图卷积由四种灵活的操作组成，并具有可学习的可微函数。与图中定义的邻居关系类似，顶点的超边缘间邻居和超边缘的顶点间邻居没有自然排序。依据上述框架，文章对四种函数进行定义，并提出HGNNConv+模型，具体定义如下：

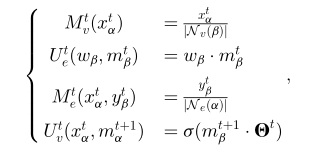
将上述函数代入通用空间超图卷积框架，以矩阵方式写出可以得到如下公式：

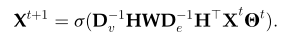
该公式即为HGNNConv+的矩阵表达式。进一步文章撰写了大量篇幅的比较，对比HGNN与GNN的区别以及HGNN的优势。

实验

为了评估所提出的超图神经网络框架的性能，进行了三种类型的实验。前两个实验分别针对具有和不具有图结构的数据设计。最后一个是针对具有超图结构的数据设计的。

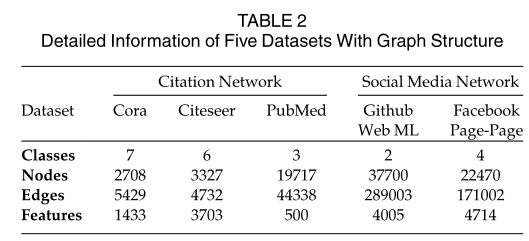
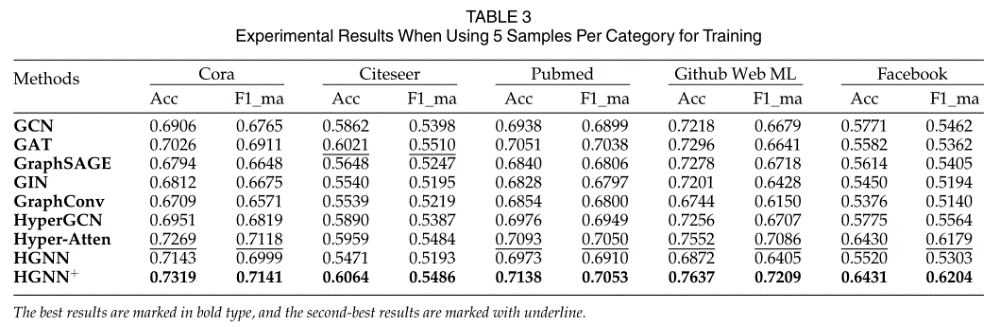
对于有图结构的数据而言，作者选择了如下数据集进行实验，数据集细节如上图所示，包括引用网络和社交媒体网络。实验结果如下所示。针对其中基于超图的方法而言，其性能较差的原因可能是其结构简化或过度参数化。HyperGCN的性能并不理想，可能是由于它简化了初始超图结构来对超图进行图卷积。这种简化是不可逆的，因此肯定会丢失关键信息。Hyper-Atten利用了hyperedge-vertex注意力模块，因此与HyperGCN相比产生了更好的性能。然而，这种复杂的注意力策略引入了大量的参数，使模型容易出现过拟合问题。HGNN+则提出了超边缘群体层面的注意机制，该机制可以考虑不同超边缘群体和顶点之间的关系，减少可学习参数的数量，从而有效防止过拟合，实现更稳定的改进。

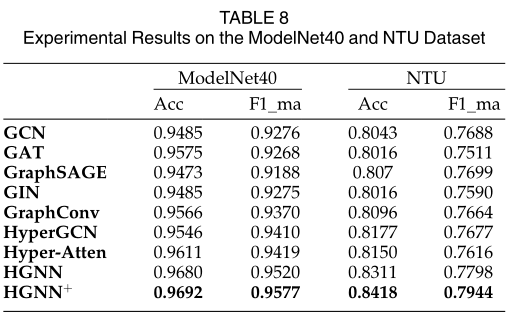
进一步，对于没有结构化数据的数据集，文章选择了两个公开的3D对象数据集，包括ModelNet40数据集和NTU数据集，结果如下所示。

结论

文章扩展了HGNN的工作，并引入了一个用于表示学习的通用超图神经网络框架HGNN+。所提出的HGNN+框架在多模态/多类型数据的高阶数据相关性建模方面具有优势。文章介绍了四种数据关联生成方法，并提出了一种自适应超边缘融合策略来生成整体超图。在空间域中引入超图卷积来学习表示。在9个数据集上的实验和与最新方法的比较表明了文章提出的方法的有效性。结果和数学讨论表明，所提出的框架能够实现新的最先进的性能，特别是当没有明确的数据相关性时。