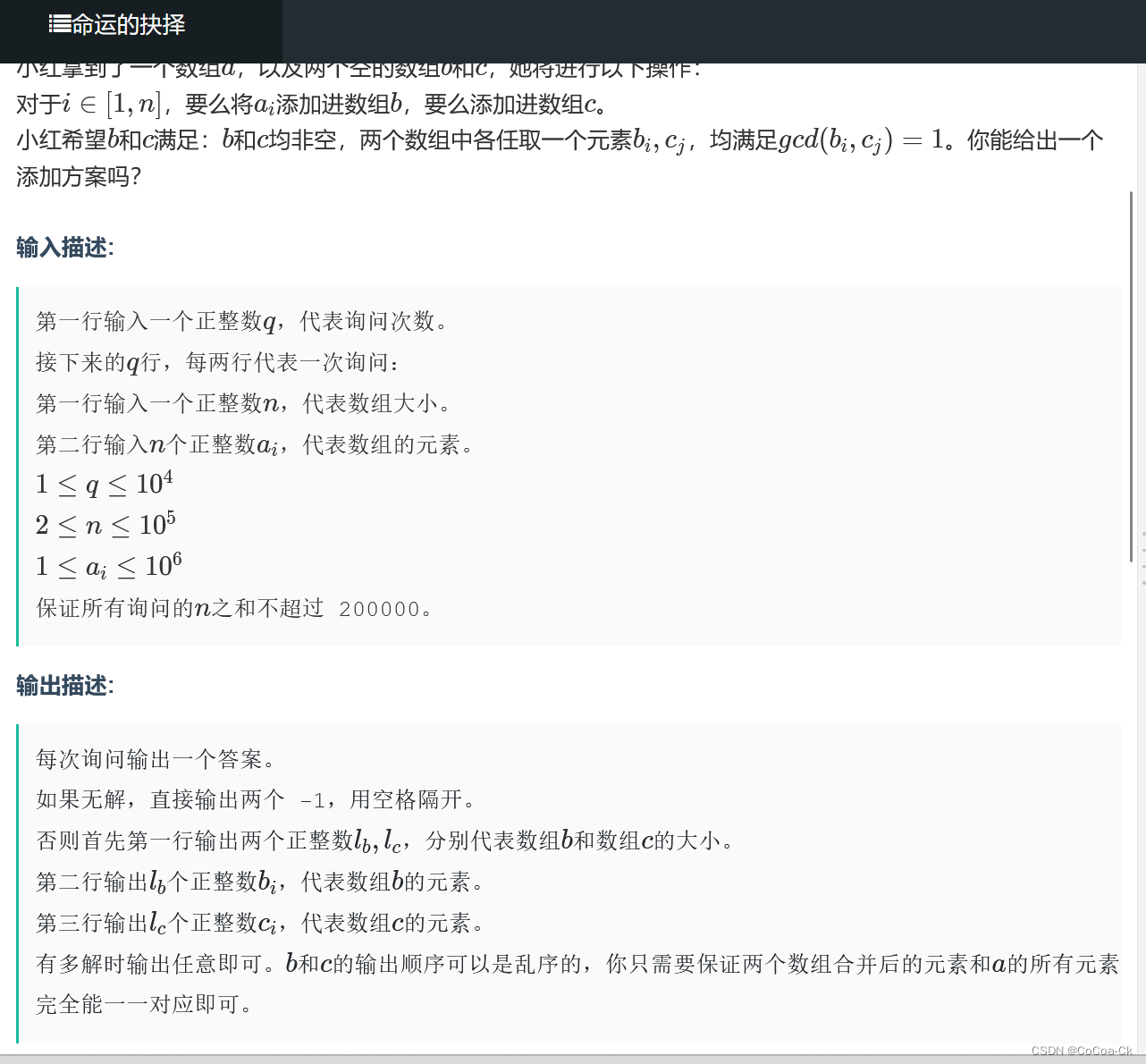
1.并查集+数学

分析：

首先我们知道算数基本定理，如果两个数有大于1的质因子，那么我们就需要把他们放在同一个集合，因此我们可以用欧拉刷出1e6范围内的素数，然后依次看输入的数。

拿20=2*2*5举例子，我们在求质数时也得到了其最大质因子，我们取出来，如过它没有访问过，那么记下第一个访问它的，假如那个质因子已经被其他数访问了，那么就用并查集合并。

然后20/5=4，我们可以得到其质因子为2，依次循环。

最后我们以第1个元素为分节点，假如他们都在同一个集合说明无法分即可。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int q,fa[100010],a[100010],pri[1000000],cnt,p[1000100],n,b[1000100];
int find(int x){if(fa[x]==x) return x;return fa[x]=find(fa[x]);
}
void solve(){for(int i=1;i<=n;i++) fa[i]=i;vector<int> A;for(int i=1;i<=n;i++){int x=a[i];while(x>1){int c=p[x];while(x%c== 0) x/=c;if(b[c]==0){b[c]=i;A.push_back(c);}else fa[find(i)]=find(b[c]);}}for(int i=0;i<A.size();i++) b[A[i]]=0;vector<int> B,C;for(int i=1; i<=n; ++i){if(find(1)!=find(i)) B.push_back(a[i]);else C.push_back(a[i]);}if(B.size()==0){cout<<-1<<" "<<-1<<endl;}else{cout<<B.size()<<" "<<C.size()<<endl;for(int i=0;i<B.size();i++) cout<<B[i]<<" ";cout<<endl;for(int i=0;i<C.size();i++) cout<<C[i]<<" ";cout<<endl;}
}
int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>q;p[1]=1;for(int i=2;i<=1000000;i++){if(p[i]==0){p[i]=i;pri[++cnt]=i;}for(int j=1;j<=cnt;j++){if(pri[j]>p[i]||i*pri[j]>1000000) break;p[i*pri[j]]=pri[j];}}while(q--){cin>>n;for(int i=1;i<=n;i++) cin>>a[i];solve();}
}

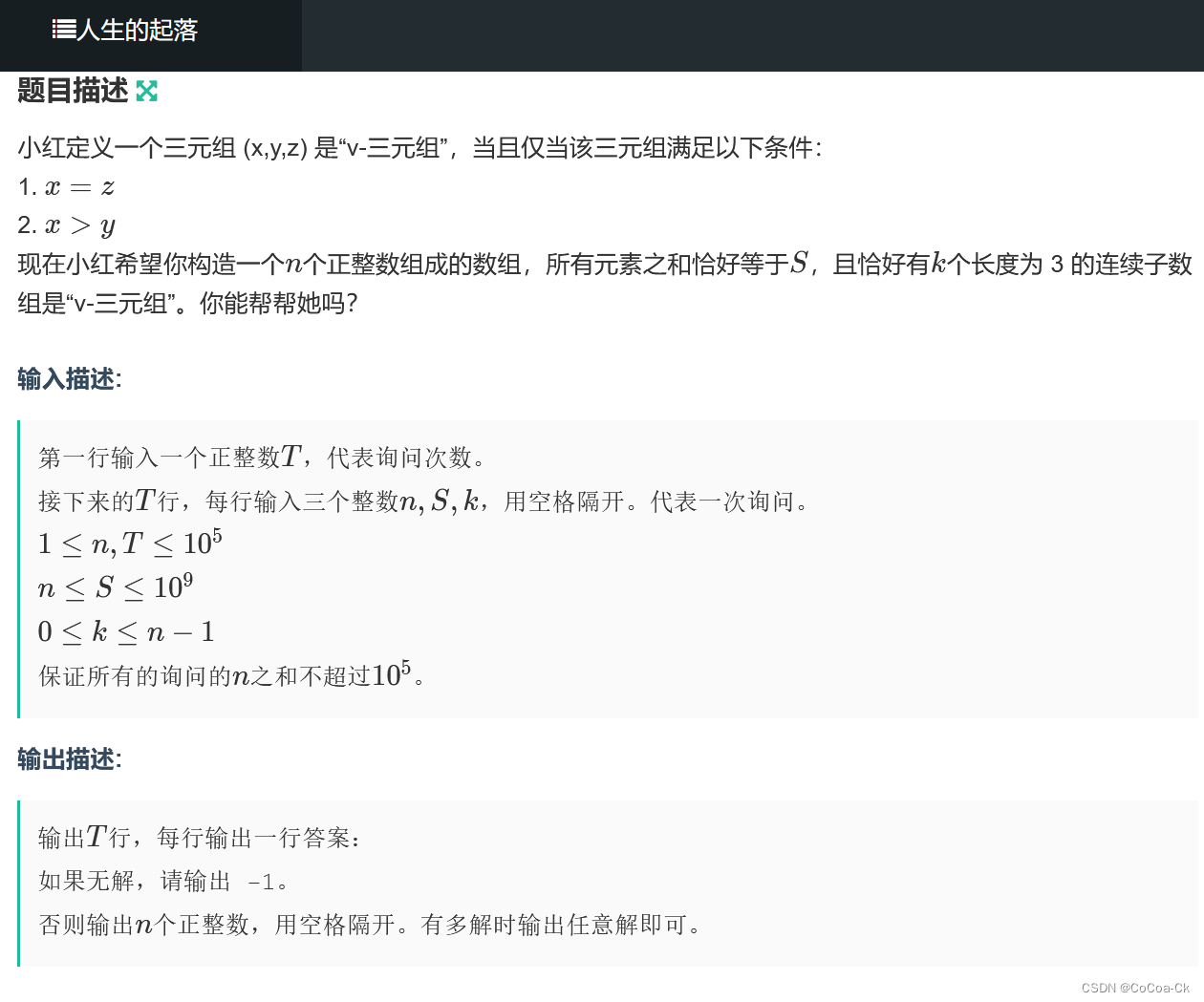
2.构造题（细节题）：

分类讨论的思想在这个题上体现的淋漓尽致。

首先我们特判k=0的情况，此时只要s>n即可，1111111，s-n.

当k!=0时，拼成k个三元组要2k+1个，此时，假如n<2k+1那就不行。

n=2k+1时，我们起先构造2,1,2,1,2这种，判断s与3k+2的关系，s<3k+2就不行，等于时可以。

大于时我们让每一个2先加一个值（给1的话就不满足关系了），加什么值呢？

一共有k+1个2，只要可以一次给出k+1，那就从答案中减（贪心一下就可以），没有时才考虑给1.

而若连给2的k+1个也给不起那肯定不行。

当n>2k+1时，我们在后面接上一段1，其开头把差值补上即可。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
long long t,n,s,k,a[100010];
void solve(){if(k==0){if(s<n){cout<<-1<<endl;return;}for(int i=1;i<=n;i++) a[i]=1;a[1]+=s-n;}else{if(n<2*k+1){cout<<-1<<endl;return;}else if(n==2*k+1){if(s<3*k+2){cout<<-1<<endl;return;}else if(s==3*k+2){for(int i=1;i<=n;i++){if(i%2==1) a[i]=2;else a[i]=1;}}else{s-=3*k+2;long long x=s/(k+1);if(x==0){cout<<-1<<endl;return; }else{for(int i=1;i<=n;i++){if(i%2==1) a[i]=x+2;else a[i]=1;}s-=x*(k+1);for(int i=1;i<=n;i++){if(i%2==0&&(s>0)){a[i]=2;s--;}if(s<0) break;}}}}else{if(s<3*k+2){cout<<-1<<endl;return;}for(int i=1;i<=2*k+1;i++){if(i%2==1) a[i]=2;else a[i]=1;}s-=3*k+2;for(int i=2*k+2;i<=n;i++){a[i]=1;s--;if(s<0){cout<<-1<<endl;return;}}a[2*k+2]+=s;}}for(int i=1;i<=n;i++) printf("%lld ",a[i]);cout<<endl;
}
int main(){cin>>t;while(t--){cin>>n>>s>>k;solve();}
}

3.构造题+DFS

首先当一个红点下面是一个红点时，它可以被忽略。

因此假如它的儿子节点只有红点或没有点，那么就不行。

而只要它有一个白点他就一定可以构造出3的倍数。

因此我们令白的所有点=1，红的为0，然后先维护一下子树和。

再DFS2一下判断红点下的子树和，若为1就自己改成2，为2的话不动，输出时改1即可。为0的话因为不能有权值为0的点，于是自己变成2，再找一个子节点变成2即可。

下面是AC代码：

#include <bits/stdc++.h>
using namespace std;
int n,x,ans[100010],sz[100010],f;
string s;
vector<int> edge[100010];
void dfs1(int root){int xx=0;if(s[root]=='W') xx++;ans[root]=xx;for(int i=0;i<edge[root].size();i++){dfs1(edge[root][i]);if(s[root]=='W') xx+=sz[edge[root][i]];}sz[root]=xx;
}
void dfs2(int root){int white=0;for(int i=0;i<edge[root].size();i++){dfs2(edge[root][i]);if(f==1) return;white+=sz[edge[root][i]];   }if(white==0&&s[root]=='R'){f=1;return;}white%=3;if(s[root]=='R'){if(white==1) ans[root]=2;if(white==0){ans[root]=2;for(int i=0;i<edge[root].size();i++){ans[edge[root][i]]=2;break;}}}
}
int main(){cin>>n>>s;s=' '+s;for(int i=1;i<n;i++){scanf("%d",&x);edge[x].push_back(i+1);}dfs1(1);dfs2(1);if(f==1) cout<<-1;else{for(int i=1;i<=n;i++) printf("%d",max(1,ans[i]));}
}

4.枚举+二维前缀和：

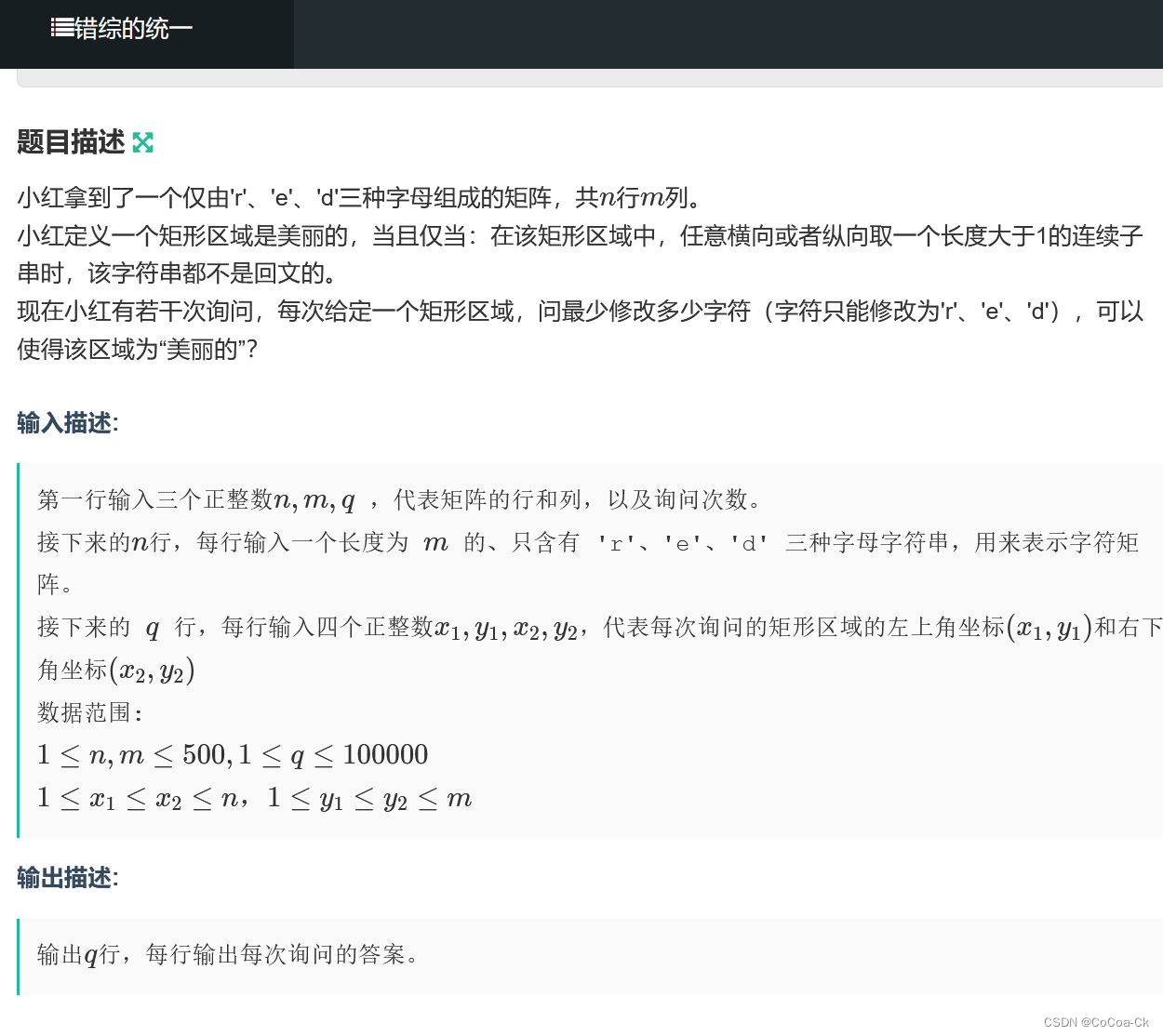
显然符合条件的只有3!*2种情况，我们先维护一下题目给的和那12个不同的地方（标为1），然后二维前缀和维护一下即可，下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,q,a[13][510][510],sum[13][510][510],x1,x2,yy1,y2;
char ti[510][510],ans[13][510][510],x;
string ss[12][3]={{"red","dre","edr"},{"red","edr","dre"},{"rde","der","erd"},{"rde","erd","der"},{"erd","der","rde"},{"erd","rde","der"},{"edr","dre","red"},{"edr","red","dre"},{"dre","red","edr"},{"dre","edr","red"},{"der","rde","erd"},{"der","erd","rde"}};
int calc(int x1,int y1,int x2,int y2,int i){return sum[i][x2][y2]-sum[i][x1-1][y2]-sum[i][x2][y1-1]+sum[i][x1-1][y1-1];
}
int main(){cin>>n>>m>>q;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf(" %c",&x);ti[i][j]=x;}}for(int i=1;i<=12;i++){for(int j=1;j<=3;j++){for(int k=1;k<=3;k++){ans[i][j][k]=ss[i-1][j-1][k-1];}}for(int j=1;j<=3;j++){for(int k=4;k<=500;k++){ans[i][j][k]=ans[i][j][k-3];}}for(int j=4;j<=500;j++){for(int k=1;k<=500;k++) ans[i][j][k]=ans[i][j-3][k];}}for(int i=1;i<=12;i++){for(int k=1;k<=n;k++){for(int j=1;j<=m;j++){if(ti[k][j]!=ans[i][k][j]) a[i][k][j]=1;}}}for(int i=1;i<=12;i++){for(int k=1;k<=n;k++){for(int j=1;j<=m;j++){sum[i][k][j]=sum[i][k-1][j]+sum[i][k][j-1]-sum[i][k-1][j-1]+a[i][k][j];}}}for(int i=1;i<=q;i++){scanf("%d%d%d%d",&x1,&yy1,&x2,&y2);int ans=n*m;for(int i=1;i<=12;i++){ans=min(ans,calc(x1,yy1,x2,y2,i));}if (x2 - x1 == 1 && y2 - yy1 == 1 && ti[x1][yy1] == ti[x2][y2] && ti[x1][y2] == ti[x2][yy1] && ti[x1][yy1] != ti[x1][y2]) ans = 0;printf("%d\n",ans);}
}