102.二叉树的层次遍历
题目链接
讲解链接
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。而这种层序遍历方式就是图论中的广度优先遍历。
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if not root:return []result = []queue = deque([root]) # 向队列中存入根结点while queue:level = [] # level用于储存每一层的结点for _ in range(len(queue)): # len(queue)为当前层中元素的数量node = queue.popleft()level.append(node.val)if node.left: # 将左孩子加入队列queue.append(node.left)if node.right: # 右孩子加入队列queue.append(node.right)result.append(level) # for循环每次结束时,代表遍历完了一层的结点,此时将level添加到result中return result
226.翻转二叉树
题目链接
讲解链接
要实现二叉树的反转,其实就是把每一个节点的左右孩子交换一下即可。关键在于遍历顺序,前中后序以及层次遍历的选择。遍历的过程中去翻转每一个节点的左右孩子就可以达到整体翻转的效果。本题使用前序、后序和层次相对容易。
递归法:
class Solution:def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:if not root:return Noneroot.left, root.right = root.right, root.left # 直接交换左右孩子self.invertTree(root.left) # 左孩子递归调用self.invertTree(root.right) # 右孩子递归调用return root # 每次返回当前根节点迭代法(前序遍历):
class Solution:def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:if not root:return Nonestack = [root]while stack:node = stack.pop()node.left, node.right = node.right, node.left # 与遍历的区别就是这步交换左右孩子if node.left:stack.append(node.left)if node.right:stack.append(node.right)return root # 返回根结点迭代法(层次遍历)
class Solution:def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:if not root:return Nonequeue = deque([root])while queue:for _ in range(len(queue)):node = queue.popleft()node.left, node.right = node.right, node.leftif node.left:queue.append(node.left)if node.right:queue.append(node.right)return root迭代法的代码与遍历的代码基本一致,仅需添加一句交换左右孩子即可。
101.对称二叉树
题目链接
讲解链接
一开始想到的做法是判断根节点的左子树和右子树的中序遍历顺序是否相同,如果相同则说明二叉树是对称的。这个做法可以涵盖大部分的情况,但在测试用例为图示的二叉树时会出错,因为在这种情况下左右子树的中序遍历顺序是相同的,但却并不对称。
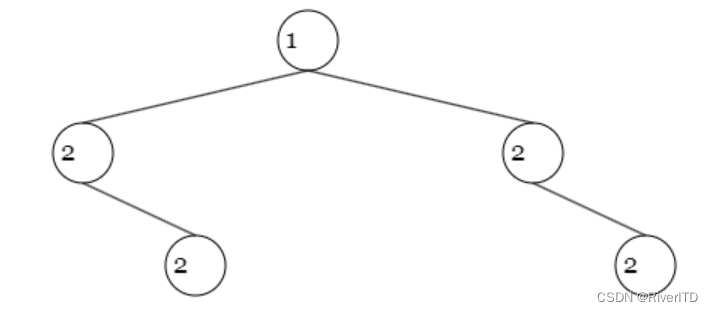
正确思路:
判断对称二叉树要比较的是哪两个节点,要比较的不是左右节点!对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,所以其实要比较的是两个树(根节点的左右子树)。这里由于需要收集左右孩子的信息向上一层返回,所以必须采用后序遍历。
class Solution:def compare(self, left, right):if not left and not right: # 左右孩子均为空,则为对称return Trueelif left and not right: # 左右孩子其中之一为空,另一个不为空,则为非对称return Falseelif not left and right:return Falseelif left.val != right.val: # 左右孩子均不为空但值不相等,为非对称return Falseelse:outside = self.compare(left.left, right.right) # 外侧情况,对应后序遍历的左inside = self.compare(left.right, right.left) # 内侧情况,对应后序遍历的右result = outside and inside # 外侧和内侧均为True,则表明二叉树是对称的,对应中return resultdef isSymmetric(self, root: Optional[TreeNode]) -> bool:if not root: # 空树是对称的return Trueresult = self.compare(root.left, root.right)return result