every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog

0. 前言

熵和交叉熵

1. 熵

概率分布的熵可以被解释为与给定分布中的随机变量相关的不确定性或缺乏可预测性的度量。

我们还可以使用熵来定义数据源的信息内容。例如，假设我们观察到由分布p生成的符号序列$X_n\sim p$。如果p具有高熵，则很难预测每个观测值Xn的值。因此我们说数据集$D=(X_1,\dots ,X_n)$具有较高的信息量。相反，如果p是一个熵为0(最小值)的简并分布，那么每个Xn都是相同的，因此D不包含太多信息。

离散随机变量X的熵定义为,
$$\begin{array}{rl}H(X)& \triangleq -\sum _{k=1}^{K}p(X=k)lo{g}_{2}p(X=k)\\ & =-\sum _{i=1}^{n}p(x_i)lo{g}_{2}p(x_i)\\ & =-E_X[lo{g}_{2}p(X)]\end{array}$$

注意，我们用符号$H(X)$来表示随机变量(rv)与分布p的熵，就像人们用$V[X]$来表示与X相关的分布的方差;我们也可以写成$H(p)$ 。通常我们使用log以2为底，在这种情况下，单位称为位(二进制数的简称)。例如，如果 X ∈ { 1 , . . . , 5 } X \in \{1,...,5\} X∈{1,...,5} 的直方图分布 $p=[0.25,0.25,0.2,0.15,0.15]$ ，我们得到 $H=2.29$ bits。如果用log以e为底的对数，单位叫做nats。

---

具有最大熵的离散分布是均匀分布。对于k元随机变量，当$p(x=k)=1/k$ 时，熵最大;在这种情况下，$H(X)=log2K$。如下：

$$H(X)=-\sum _{k=1}^K\frac{1}{K}log(1/K)=-log(1/K)=log(K)$$

相反，具有最小熵(零)的分布是将其所有质量置于一个状态的任何delta函数。这样的分布没有不确定性。

---

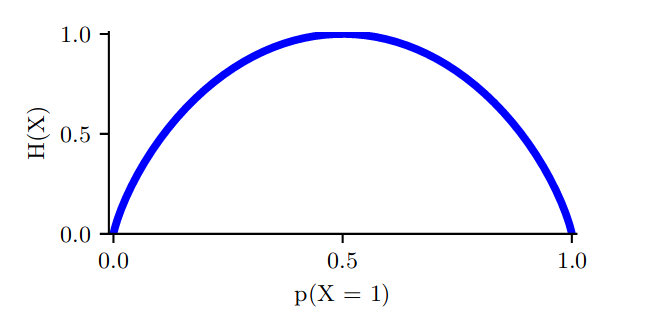
对于二元随机变量 X ∈ { 0 , 1 } X \in \{0,1\} X∈{0,1} 的特殊情况，我们可以写成 $p(X=1)=\theta$ 和 $p(X=0)=1-\theta$ 。因此熵就变成了,

$$\begin{array}{rl}H(X)& =-[p(X=1)lo{g}_{2}p(X=1)+p(X=0)lo{g}_{2}p(X=0)]\\ & =-[\theta lo{g}_2\theta +(1-\theta )lo{g}_2(1-\theta )]\end{array}$$

这叫 binary entropy function, 可以写成$H(\theta )$,图如下：

2. 相对熵（KL散度）

2.1 概念

考虑一个未知的分布$p(x)$，假定用一个 近似的分布$q(x)$ 对其进行建模。

如果我们使用 q(x) 来建立一个编码体系，用来把 x 的值传给接收者，那么由于我们使用了q(x)而不是真实分布p(x)，平均编码长度比用真实分布p(x)进行编码增加的信息量(单位是 nat )为：
$$\begin{array}{rl}KL(p||q)& =-\int p(x)log(q(x))dx-(-\int p(x)log(p(x))dx)\\ & =-\int p(x)log(\frac{q(x)}{p(x)})dx\\ & =\int p(x)log(\frac{p(x)}{q(x)})dx\end{array}$$

这被称为分布p(x)和q(x)之间的相对熵，也被称为KL散度。

上式为连续型随机变量的KL散度，下式为离散型随机变量的KL散度。

$$KL(p||q)=\sum p(x)log(\frac{p(x)}{q(x)})$$

2.2 性质

1. 不对称;

$$KL(p||q)\ne KL(q||p)$$
2. 非负,当且仅当p(x) = q(x)时取到等号成立；
$$KL(p||q)\ge 0$$

2.3 KL散度和最大似然

假 设 数 据 通 过 未 知 分 布$p(x)$生 成， 我 们 想 要 对$p(x)$建 模。 我 们 可 以 试 着 使 用 一 些 参 数 分 布$q(x|\theta )$来近似这个分布。$q(x|\theta )$由可调节的参数$\theta$控制（例如一个多元高斯分布）。

一种确 定$\theta$的方式是最小化$p(x)$ 和 $q(x|\theta )$ 之间关于$\theta$的Kullback-Leibler散度。我们不能直接这么做，因 为我们不知道p(x)。

但是，假设我们已经观察到了服从分布p(x)的有限数量的训练点$x_n$，其 中$n=1,...,N$ 。那么，关于p(x)的期望就可以通过这些点的有限加和

$$\begin{array}{rl}KL(p||q)& =\sum _{n=1}^{N}p(x_n)log(\frac{p(x_n)}{q(x_n|\theta )})\\ & \simeq \frac{1}{N}\sum _{n=1}^N[logp(x_n)-log(q(x_n|\theta ))]\end{array}$$

公式左侧和$\theta$无关，第一项是使用训练集估计的分布$q(x|\theta )$下的$\theta$的负对数 似然函数。

因此我们看到，最小化Kullback-Leibler散度等价于最大化似然函数。

2.4 交叉熵

交叉熵公式：

$$H(p,q)=-\sum _{i}p(x_i)logq(x_i)$$

而我们的KL散度公式：

$$\begin{array}{rl}{D}_{KL}(p||q)& =\sum _{i}p(x_i)log(\frac{p(x_i)}{q(x_i)})\\ & =\sum _{i}p(x_i)logp(x_i)-\sum _{i}p(x_i)logq(x_i)\\ & =H(p,q)-H(p)\end{array}$$

即，交叉熵 = KL散度 + 熵。
$$H(p,q)=D_{KL}(p||q)+H(p)$$

参考

1. https://zhuanlan.zhihu.com/p/372835186
2. https://zhuanlan.zhihu.com/p/39682125
3. https://zhuanlan.zhihu.com/p/365400000
4. https://blog.csdn.net/yg2685482622/article/details/108273329
5. https://zhuanlan.zhihu.com/p/292434104