数学基础(变换矩阵,向量运算等)
1.变换矩阵总结
一切物体(包括模型,向量等)的缩放,旋转,平移,切变等,都可以通过变换矩阵得到。在投影(projection)变换时也有很多应用。
本节简单的介绍一下变换矩阵
1.1 旋转
旋转在几何和线性代数中是描述刚体围绕一个固定点的运动的在平面或空间中的变换
我们这里只讨论“坐标系保持不动,向量绕坐标轴旋转”的观点。
因为当旋转与平移进行结合时,会因为先后顺序发生不同的情况
(先平移后旋转,物体的位置会因旋转而发生变换,原因是在平移后坐标空间发生的变化,因此再使用旋转矩阵进行变换是相对于世界空间原点进行变换的)

(先旋转后平移,物体的位置不会因为旋转而发生变化,原因是在平移前,已经做了旋转变换,因此旋转时物体本身坐标空间还在世界中心。)

回到正题

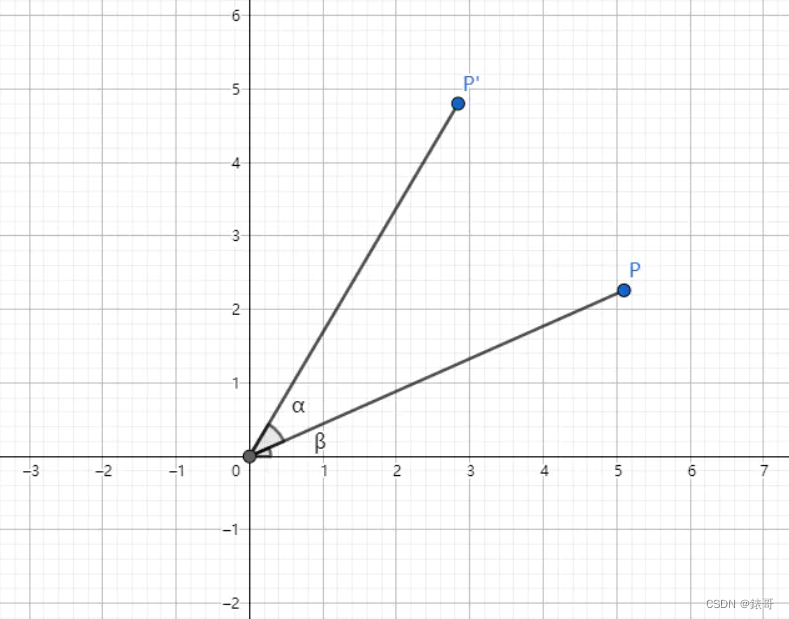
由于涉及到角度,所以可以把笛卡尔坐标系转换到极坐标系,设r为极半径,则P点坐标为
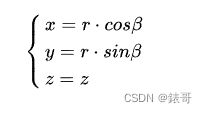
相应的,P’点坐标为
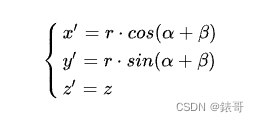
根据三角函数公式,联立两个方,可知,P’关于x,y的方程为:
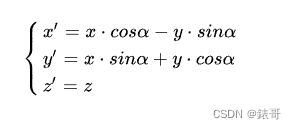
用4x4矩阵可以表述为:

即,绕Z轴旋转的变换矩阵为:
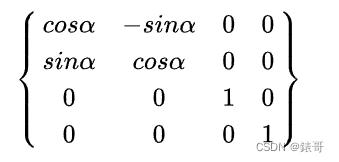
同理可得下面几个常见的旋转变换矩阵:

其中逆时针是正方向,当顺时针旋转时,角度可以取负的正方向,之后根绝三角函数的奇偶性即可进行转换(意思是只要记住逆时针旋转的公式就行了)
1.2缩放
缩放在欧式空间中是描述延一个或多个坐标轴方向的缩放因子放大或者缩小物体的线性变化
每一个坐标轴方向都有其单独的缩放因子。
各坐标轴缩放因子不同,缩放后结果的形状可能发生变化,此时的缩放被叫做方向缩放。
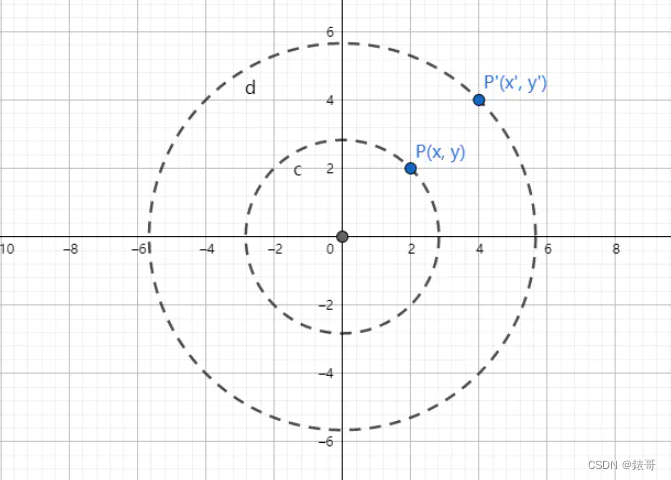
如图,我们已知P点坐标,则P’点的坐标可以表示为:

用4x4矩阵表示为:
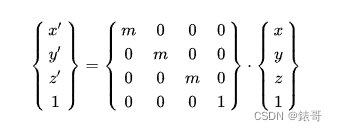
所以,三维缩放变换矩阵为:[外链图片转存失败,源站可能有防盗在这里插入链机制,建描述]议将图片上https://传(imbg.csdnimg.cn/9c92cd97df154zPXT1688c7a164b2a4f00f.pg08)(https://img-log.csdnimg.cn/9c92cd97df1541688c7a164b2a4f800f.png)]
1.3平移
平移在仿射空间中指物体延同一方向移动相同距离的变换
平移是一种等距同构的变换,可以被视为某一向量施加于物体没一点的结果。即,设v是已知向量,P为空间中一点,则平移:
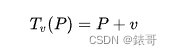
如下图所示:
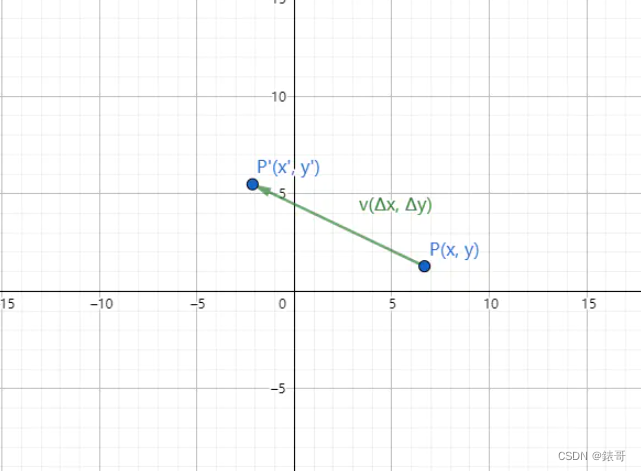
用4x4矩阵表示为
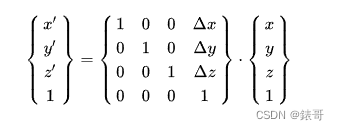
即平移变换矩阵为:

1.4 投影
投影是指一个从向量空间V映射到它自身的线性变换。
投影是生活中“平行投影”概念的形式化和一般化。例如,在现实生活中,阳光照射物体在地面留下的影子。我们假设阳光是沿着同一方向(平行且垂直于地面的)照射物体,地面是严格的平面。那么,这就是投影最直观的例子。
1.5总结
适用于列向量的4x4矩阵形式
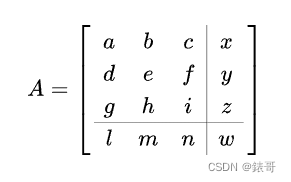
这里的x,y,z与平移相关,分别是x,y,z轴的平移量。
a,b,c,d,e,f,g,h,i与线性变换相关。
l,m,n与透视投影变换相关。
为什么仿射变换要升维度?
线性变换在几何直观上有如下特点:
变换前后,直线仍然保持是直线的状态
变换前后,原点保持固定,不会变化
是因为我们无法通过矩阵的实现平移操作,平移会改变向量空间。
仿射变换,又称仿射映射,是指在几何中,对一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。
仿射变换相比于线性变换,不需要保证变换前后坐标原点不变。
我们希望能通过矩阵的乘法实现一个通用的计算模式,来进行坐标点的变化。
因此就需要齐次坐标:齐次坐标的本质就是升维来解决问题。
通过增加一个维度,可以在高维度上,通过线性变换来处理低维度的仿射变换。

2.向量点乘,叉乘的定义及几何意义
2.1 向量点乘
点乘的数学定义: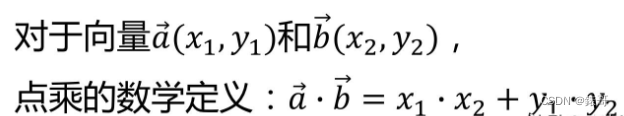
点乘的几何意义:两个单位向量之间夹角的余弦值。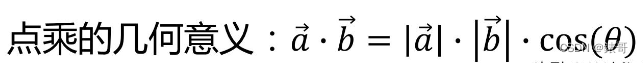
2.2 向量叉乘
参考:https://www.jianshu.com/p/ccdee786acbd
http://www.360doc.com/content/19/1222/18/40070800_881412732.shtml
https://juejin.cn/post/6886474840111317005
https://www.jianshu.com/p/c3e887c4c4f4
3.欧拉角与四元数与万向节死锁
欧拉角:
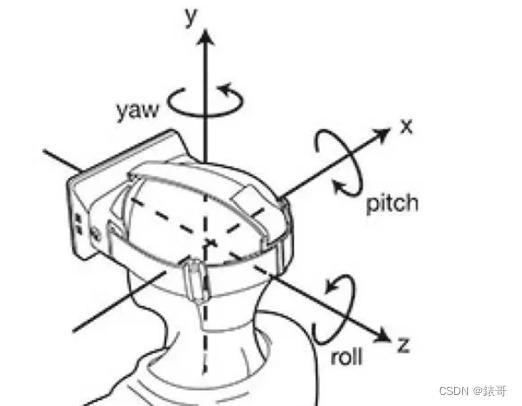
pitch俯仰角:点头,x轴为旋转轴。
yaw偏航角:左右摇头,y轴为旋转轴
roll滚动角:向日葵(招手)式的摇头,z轴为旋转轴。

经典面试题:欧拉角定义的旋转矩有什么问题,怎么处理?
欧拉角定义了绕着三个坐标轴的旋转角,来确定刚体的旋转位置的方式,包括俯仰角pitch,偏航角yaw和滚动角roll;
它的优点是比较直观,而且单个维度上的角度上比较容易插值;
缺点是它不能进行任意方向的插值,而且会导致万向节死锁的问题,旋转的次序也会对结果产生影响,也就是在旋转过程中会损失自由度。
我们依次绕坐标系x,y,z轴旋转,当绕y轴旋转90度后,z轴就指向了原来的x轴,这样一来。事实上只绕了x和y两个轴旋转,第三个轴的自由度缺失了。
四元数:
我们使用四元数一般就是简单的用来进行三维旋转,记住下面的几个公式:
首先,定义一个需要做的旋转。旋转轴为向量v = (vx,vy,vz),旋转角度为θ(右手法则的旋转)。
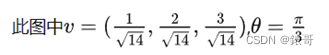
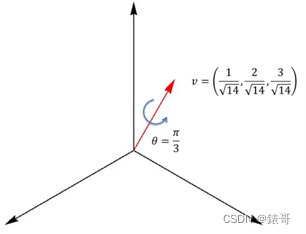
那么与此相对应的四元数(下三行式子都是一个意思,只是不同的表达形式)。
注意角度都是θ/2。
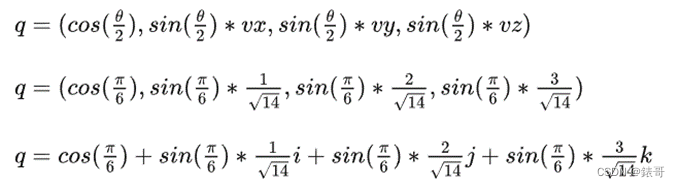
这是它的共轭(下三行式子都是一个意思,只是不同的表达形式)。
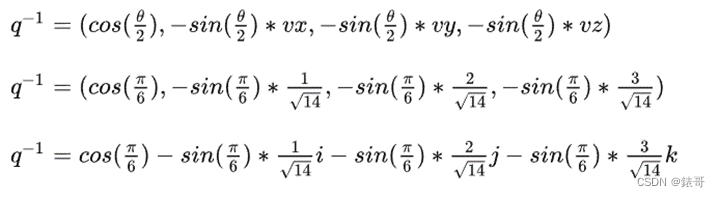
如果你想算一个点w = (wx,wy,wz)在这个旋转下新的坐标W’,需要进行如下操作。
-
- 定义纯四元数
qw = (θ,wx,wy,wz) = θ+wxi+wyj+wz*k
- 定义纯四元数
-
- 进行四元数运算
qw’ = q x qw x q-1
- 进行四元数运算
-
- 产生的qw’一定是纯四元数,也就是说它的第一项为θ,有如下形式:
qw’ = (θ,wx’,wy’,wz’) = θ + wx’*i+wy’*j+wz’*k
- 产生的qw’一定是纯四元数,也就是说它的第一项为θ,有如下形式:
-
- qw’中的后三项(wx’,wy’,wz’)就是w’:
w’ = (wx’,wy’,wz’)
- qw’中的后三项(wx’,wy’,wz’)就是w’:
这样一来,就完成了一次四元数旋转运算。
同理,如果你有一个四元数:
q = (q1,q2,q3,q4) =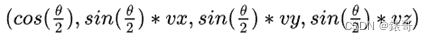
那么,它对应一个以向量v = (vx,vy,vz)为轴旋转θ角度的旋转操作(右手法则的旋转)。
其他小记:
其实还有一些比较重要的数学上的知识,比如说MVP矩阵的推导,尤其是
VP矩阵的推导
三角形插值,透视插值矫正,光线追踪求交等。
都略知一二,但是都不是很深入,有待整理提高。
慢慢的往上加,但是一般在后面的章节里都有记载。





![[自动化测试] 读取CSV 文件](https://img-blog.csdnimg.cn/5d56cba78d64410eaf5279e6cde41f93.png)
