4.1.2 猴子吃桃

【问题】一只猴子摘了很多桃子，每天吃现有桃子的一半多一个，到第10天时只有一个桃子，问原有桃子多少个?

【想法】设an表示第n天桃子的个数，猴子吃桃问题存在如下递推式：

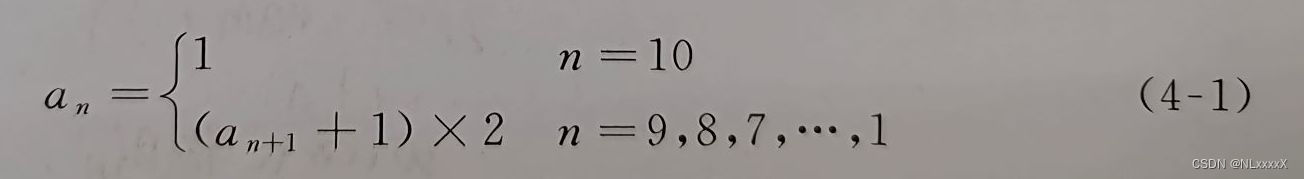
【算法实现】由于每天的桃子个数依赖于前一天的桃子个数，属于逆推法。设函数 MonkeyPeach 实现猴子吃桃问题，变量num 表示桃子的个数，程序如下。

#include <iostream>
using namespace std;

int MonkeyPeach(int n)
{
int i, num = 1;
for (i = n - 1; i >= 1; i--)
num = (num + 1) * 2;
return num;
}
int main( )
{
int n,m;
cin>>n;
m=MonkeyPeach(n) ;
cout<<"原有桃子"<<m<<"个"<<endl;
return 0;

}

【算法分析】显然，算法MonkeyPeach的时间复杂度是O(n)

4.2.1 Fibonacci数列

【问题】把一对兔子(雌雄各1只)放到围栏中，自第2个月起，每个月这对兔子都会生出一对新兔子，其中雌雄各1只，而且每对新兔子自第2个月起每个月也会生出一对新兔子，也是雌雄各1只。问一年后围栏中有多少对兔子?

【想法】令Fn表示第n个月围栏中兔子的对数，显然第1个月有1对，由于每对新兔子在第2个月后才可以生兔子，因此，第2个月仍然有1对，第n个月时，那些第n-1个月就已经在围栏中的兔子仍然存在，第n-2个月就已经在围栏中的每对兔子都会生出一对新兔子，即Fn=Fn-1+Fn-2。因此，Fibonacci(斐波那契)数列存在如下递推关系式：


【算法实现】设函数Fibonacci参解第n个月兔子的对数，变量1和f2分别存储第n-1和n-2个月兔子的对数，程序如下。

#include <iostream>
using namespace std;

int Fibonacci(int n)
{
int f, f1 = 1, f2 = 1, i;
for (i = 3; i <= n; i++)
{
f = f1 + f2; f2 = f1; f1 = f;
}
return f;
}
int main( )
{
int n;
cout << "请输入月份：";
  cin >> n;
    cout<<"第"<<n<<"个月有"<<Fibonacci(n)<<"对兔子"<<endl; 
    return 0;
}

【算法分析】显然，算法Fibonacci的时间复杂度是O(n)