0.随便说说

字符串学的太差了，每次字符串算法都是学完了就忘，正好上场$cfdiv1B$考了一个$Manacher$，就先复习它了。

1.一些概念

子串$(substring)$：一个字符串中的任意一段连续的字符串称为子串。
回文串：从左到右读和从右到左读是一样的串叫做回文串。比如：$aaa,aba,a,abba$都是回文串，而$abb,ab$等不是回文串。
回文子串：顾名思义，一个子串如果它同时也是回文串那么我们称这个子串为原串的回文子串。
回文半径：对于长度为奇数的回文串我们定义回文半径为长度$/2+1$，长度为偶数的定义为长度$/2$。

$Manacher$用于处理与回文子串相关的问题，它可以在$O(n)$的时间内得到所有回文串的首尾位置，即找到所有的数字对$(i,j),$使得$s[i,i+1,...,j]$是原串$s$的一个回文子串。

2.两个小$trick$

由于这样的回文子串个数最多有$n^2$级别，因此看似没有线性的做法。但是我们通过以下两种小技巧来化简问题。

$(1)$在所有字符的前后加上一个与原串无关的字符，原来是回文的串经过操作仍是回文串，并且长度变为奇数。
我们通过这样的一个操作将所有的回文串都转化成了长度为奇数的回文串。
$(2)$通过上述操作，我们只需要记录新串的奇回文串即可记录原串的所有回文串，因此我们可以通过一种更紧凑的方式来维护回文串位置信息。
我们记$p[i]$代表以$i$为回文中心能构成最长的回文串的回文半径。这样我们就将以$i$为回文中心的奇回文串全部记录了下来。

3.算法流程

$Manacher$的结果是求出用第一种技巧形成的新串的所有$p$值，具体是通过递推的形式求解的。在递推的同时维护当前已经计算过的回文串中右端点最大的位置$r$，和该串的回文中心$pos$。

当前我们要计算$p[i]$，则已经计算好了$p[0,1,...,i-1]$，并且有了当前计算过的回文串中最大的右端点$r$和该串的回文中心$pos$。

我们进行分类讨论，如果当前$i>r$，那么我们暴力进行求解$p[i]$，并利用$p[i]$更新新的回文串最大右端点和其回文中心。
如果$i\le r$，那么如图，一定会在之前记录的回文串找到和$i$相对应的位置$now$。
图丑见谅~

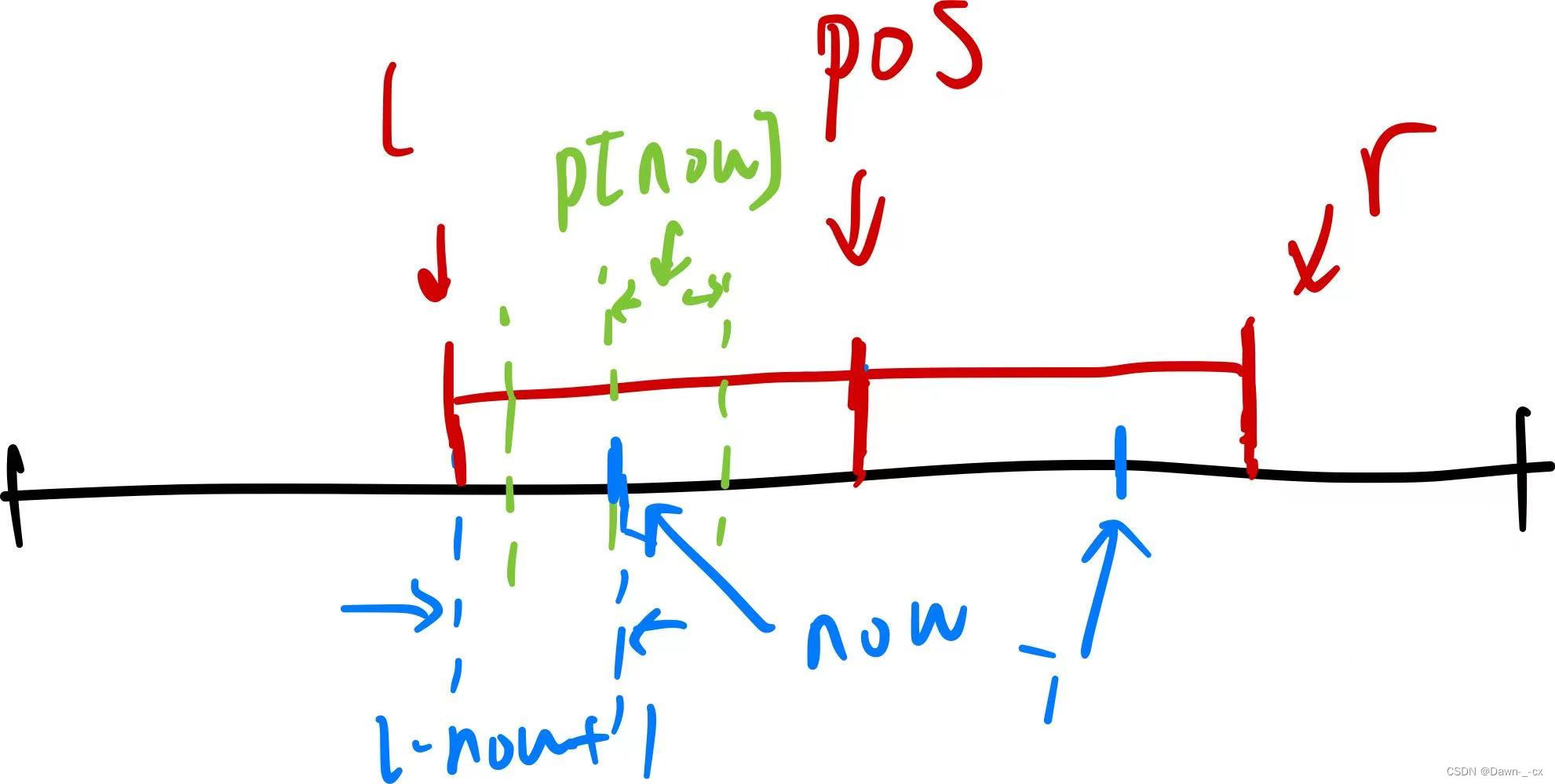
我们设具有最大右端点$r$，回文中心为$pos$的那个串的左端点为$l$。
如果$p[now]\le now-l+1$，那么很显然我们直接令$p[i]=p[now]$即可。
如果$p[now]>now-l+1$，那么我们令$p[i]=now-l+1$，并继续暴力求解$p[i]$，然后更新$r$。

这样分类讨论有点麻烦，我们观察可以发现，对于$i\le r$，可以直接令 p [ i ] = m i n { p [ n o w ] , n o w − l + 1 } p[i]=min\{p[now],now-l+1\} p[i]=min{p[now],now−l+1}，并暴力求解$p[i]$后更新$r$即可。

4.复杂度分析

由于右端点$r$最多只会扩展$n$次，因此时间复杂度为线性的$O(n)$。

5.例题

这里例题三道题用的是洛谷题单$Part5.3Manacher$，另一道是最近一场$cfdiv1$遇到的。

luoguP3805 【模板】manacher

题面
$Manacher$模板题，不适合检测模板，数据太水，我第一次打的时候当时把维护最大右端点的回文串理解成了维护最长的回文串还是过了，后面用第三题才测出来板子的问题。
$Manacher$过程中或者结束后维护一下最大的$p[i]$，计算一下就行。
上我精心缩减的代码↓

#include<bits/stdc++.h>
using namespace std;
const int N = 1e7 + 1e6 + 100;
char str[N<<1],s[N<<1];
int p[N<<1],len,n,l,r,pos;
int main(){scanf("%s",str);n=strlen(str);s[0]='!',s[++len]='$';for(int i=0;i<n;i++)s[++len]=str[i],s[++len]='$';s[++len]='$';p[0]=1,r=0,pos=0;int ans=0;for(int i=1;i<=len;i++){if(i>=r)p[i]=1;else p[i]=min(p[pos*2-i],r-i+1);while(s[i+p[i]]==s[i-p[i]])p[i]++;int nowr=i+p[i]-1;if(r<=nowr)r=nowr,pos=i;if(p[i]-1>ans)ans=p[i]-1;}cout<<ans<<endl;
}

luoguP4555 [国家集训队] 最长双回文串

题面
首先用$Manacher$求出所有的$p[i]$，再利用一个和$Manacher$维护$r$的类似的思想维护出$le[i],ri[i]$两个数组，分别代表以$i$结尾的最长的回文串，和以$i$开头的最长的回文串，最后再遍历一遍$i$即可。
这个题洛谷输入好像有空格还是啥，第一次直接输入是错的，就改成$getchar$输入了，也有可能是第一遍别的地方打错了。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 100;
char a[N<<1],s[N];
int p[N<<1],len,n,le[N<<1],ri[N<<1];
int main(){memset(le,-1,sizeof le);memset(ri,-1,sizeof ri);char ch=getchar();while(ch<'a'||ch>'z')ch=getchar();while(ch>='a'&&ch<='z')s[len++]=ch,ch=getchar();for(int i=0;i<len;i++)a[++n]=s[i],a[++n]='$';a[0]='$',p[0]=1;int pos=0,r=0,ans=2,pl=0,pr=0;for(int i=1;i<=n;i++){if(i>r)p[i]=1;else p[i]=min(p[2*pos-i],r-i+1);for(int j=p[i]+1;j<=n;j++){if(i+j-1>n||i-j+1<0)break;if(a[i+j-1]!=a[i-j+1])break;p[i]=j;}int nowr=i+p[i]-1;if(nowr>=r)pos=i,r=nowr;}for(int i=0;i<=n;i++){for(int j=i+p[i]-1;j>=i;j--){if(le[j]!=-1)break;le[j]=2*(j-i)+1;}}for(int i=n;~i;i--){for(int j=i-p[i]+1;j<=i;j++){if(ri[j]!=-1)break;ri[j]=2*(i-j)+1;}}for(int i=1;i<n;i++){if(a[i]!='$')continue;ans=max(ans,le[i]+ri[i]-2>>1);//cout<<i<<" "<<ans<<endl;}cout<<ans<<endl;}

luoguP1659 [国家集训队] 拉拉队排练

题面
还是利用$Manacher$求出所有的$p[i]$，本题要求的是奇回文串的长度，对于位置$i$，如果在我们新串中不是以特殊字符出现的，那么其在原串对应的是以其为回文中心的奇回文串。
本题所求是所有奇回文串的长度，并将前$K$个乘起来求答案，那么我们开一个桶记录奇回文串的长度个数，对于位置$i$的$p[i]$，相当于在长度为$1,3,...,p[i]$位置加$1$，那么我们可以开一个差分数组来维护这个过程，最后再用快速幂快速求解长度相同的乘积。
代码↓ 写的稍微有点丑

#include<bits/stdc++.h>
using namespace std;
const int mod = 19930726;
const int N = 1e6 + 100;
typedef long long ll;
char s[N<<1];
int p[N<<1],len,n;
ll t[N];
ll k;
int qpow(int x, ll y){int re=1;while(y){if(y&1)re=1ll*re*x%mod;x=1ll*x*x%mod,y>>=1;}return re;
}
int main(){cin>>n>>k;char chr;for(int i=1;i<=n;i++){chr=getchar();while(chr<'a'||chr>'z')chr=getchar();s[i*2-1]=chr;s[i*2]='$';}s[0]='$',n<<=1;int pos=0,l=0,r=0;for(int i=1;i<=n;i++){if(i>r)p[i]=1;else p[i]=min(p[2*pos-i],r-i+1);for(int j=p[i]+1;j<=n;j++){if(i+j-1>n||i-j+1<0)break;if(s[i+j-1]!=s[i-j+1])break;p[i]=j;}int nowl=i-p[i]+1,nowr=i+p[i]-1;if(nowr>=r)r=nowr,l=nowl,pos=i;int ri=p[i]-1,le;if(ri&1)le=1;else continue;t[le]++,t[ri+2]--;}n>>=1;int ans=1;for(int i=3;i<=n;i+=2)t[i]+=t[i-2];for(int i=n;i;i--){//cout<<i<<" "<<t[i]<<endl;if(t[i]){if(t[i]>k)ans=1ll*ans*qpow(i,k)%mod,k=0;else ans=1ll*ans*qpow(i,t[i])%mod,k-=t[i];}}if(k)puts("-1");else printf("%d\n",ans);
}

第四个题还没改完，改完了补回来，机房有点冷先回宿舍了，回去补上。