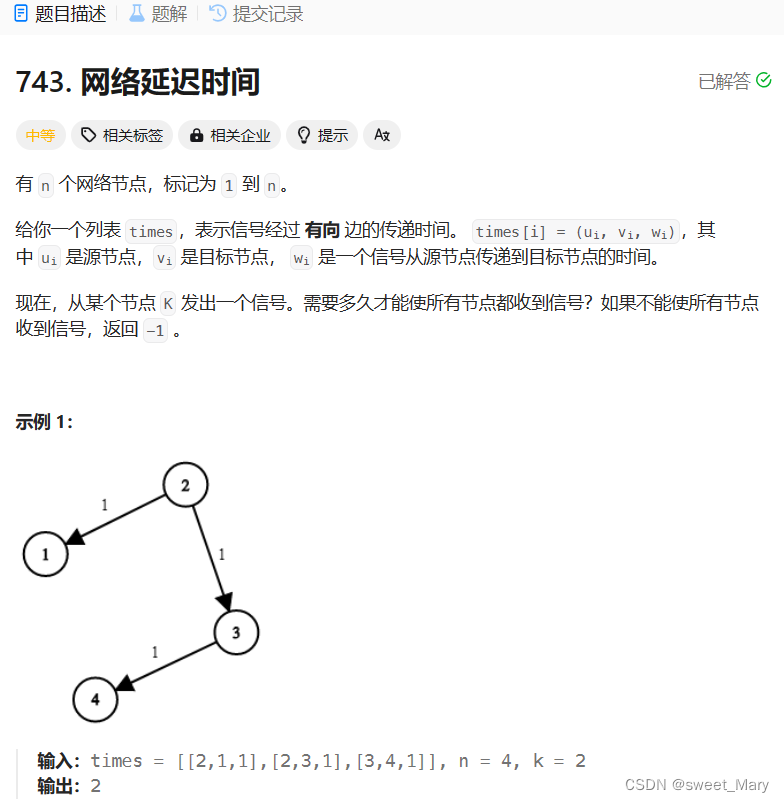
首先推荐博客：图论最短路径专题（力扣743、5888）_力扣 最短路径-CSDN博客 

迪杰斯特拉算法：

太久没有做图论的题了，，临时抱佛脚。。

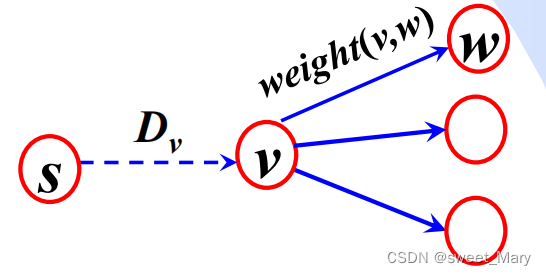
这道题可以转化为max{点x到点k的距离}。因为带权图（权值为正），无环，求最短路径的情况，迪杰斯特拉分为两个步骤：首先是初始化数组（G：二维数组，记录初始时刻点与点之间的距离，dist：每个点距k点的距离，visit：每个点是否已经确认距k点的距离）。第二部是一个大循环，即将n个点全部更新距k点的距离。再循环中，分为三个小步骤：第一点是寻找距k点距离最短的点（且该点距离k的距离还没有确定），第二点是将该点放入已知距k点距离的集合内（即visit[jj]=1），第三点是更新jj临近的那些点（距离k的距离还没有确定）距离k点的值。

参考PPT：

代码：

C++：

class Solution {
public:int networkDelayTime(vector<vector<int>>& times, int n, int k) {int inf=INT_MAX;vector<vector<int>> G(n+1,vector<int>(n+1,inf));vector<int> dist(n+1,inf);//k距离其他结点的距离vector<int> visit(n+1,0);//结点x是否已经确定最短距离int res=0;/*初始化*/int len=times.size();for(int i=0;i<len;i++){G[times[i][0]][times[i][1]]=times[i][2];}for(int i=1;i<=n;i++){G[i][i]=0;}dist[k]=0;/*正式迪杰斯特拉*/ //要更新n个结点for(int i=1;i<=n;i++){int min=INT_MAX;int jj=-1;/*找到距离k最短的距离*/for(int j=1;j<=n;j++){if(visit[j]==0 && dist[j]<min){jj=j;min=dist[j];}}/*visit[]*/if(jj==-1){return -1;}visit[jj]=1;res=max(res,min);/*更新以jj为头结点的距离*/for(int j=1;j<=n;j++){if(G[jj][j]!=INT_MAX && visit[j]==0 && dist[j]>dist[jj]+G[jj][j]){dist[j]=dist[jj]+G[jj][j];}}}return res;}
};

Python：

class Solution:def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:G=[[float("inf") for _ in range(n+1)] for _ in range(n+1)]dist=[float("inf")]*(n+1)visit=[0]*(n+1)res=0len_=len(times)for i in range(len_):G[times[i][0]][times[i][1]]=times[i][2]for i in range(1,n+1):G[i][i]=0dist[k]=0for i in range(1,n+1):min_=float("inf")jj=-1for j in range(1,n+1):if visit[j]==0 and dist[j]<min_:jj=jmin_=dist[j]if jj==-1:return -1visit[jj]=1res=max(res,min_)for j in range(1,n+1):if G[jj][j]!=float("inf") and visit[j]==0 and dist[j]>dist[jj]+G[jj][j]:dist[j]=dist[jj]+G[jj][j]return res

Floyd算法：

Floyd算法不能有环，允许有带负权值的边，但不允许有包含带负权值的边组成的回路
采用动态规划的思想，用结点k来更新结点i，j之间的距离：G[i][j]=?=G[i][k]+G[k][j]，用三层for循环来实现

参考PPT：

代码：

C++：

class Solution {
public:int networkDelayTime(vector<vector<int>>& times, int n, int k) {int inf=INT_MAX/2;vector<vector<int>> G(n+1,vector<int>(n+1,inf));/*初始化*/int len=times.size();for(int i=0;i<len;i++){G[times[i][0]][times[i][1]]=times[i][2];}for(int i=1;i<=n;i++){G[i][i]=0;}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(G[i][j]>G[i][k]+G[k][j]){G[i][j]=G[i][k]+G[k][j];}}}}/*求结果*/int res=0;for(int i=1;i<=n;i++){res=max(res,G[k][i]);}if(res==INT_MAX/2){return -1;}return res;}
};

Python：

class Solution:def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:G=[[float("inf") for _ in range(n+1)] for _ in range(n+1)]len_=len(times)for i in range(len_):G[times[i][0]][times[i][1]]=times[i][2]for i in range(1,n+1):G[i][i]=0for kk in range(1,n+1):for i in range(1,n+1):for j in range(1,n+1):if G[i][j]>G[i][kk]+G[kk][j]:G[i][j]=G[i][kk]+G[kk][j]res=0for i in range(1,n+1):res=max(res,G[k][i])if res==float("inf"):return -1return res

注意是，应该是：（不要用k哦）

for kk in range(1,n+1)

明天继续更用Bellman Ford解决该题的解法。