一、优先级队列的定义和存储
优先级队列定义:优先级高的元素在队头,优先级低的元素在队尾
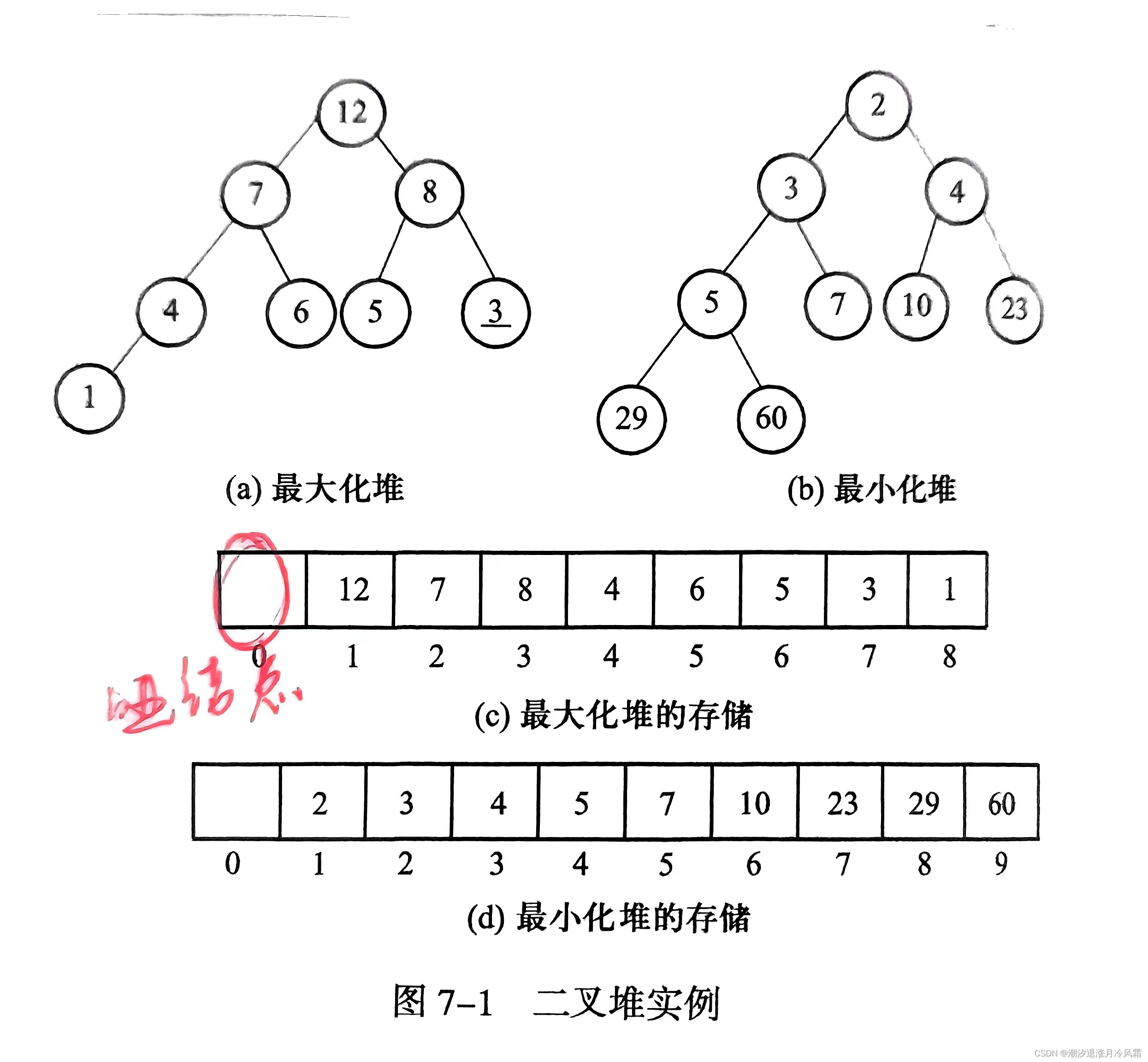
基于普通线性表实现优先级队列,入队和出队中必有一个时间复杂度O(n),基于二叉树结构实现优先级队列,能够让入队和出队时间复杂度都为O(logn),这种基于树状结构的优先级队列也称为二叉堆。当根结点为最大元素时,称为最大化堆或大顶堆;当根结点为最小元素时,称为最小化堆或小顶堆。二叉堆是有序的完全二叉树,使用顺序存储,留出数组第一个位置作为哑结点,如图所示:
二、优先级队列的运算实现
先学习优先级队列的两大核心运算:入队和出队,之后再介绍如何建堆。下面以小顶堆为例分析。
2.1 入队:上滤插入
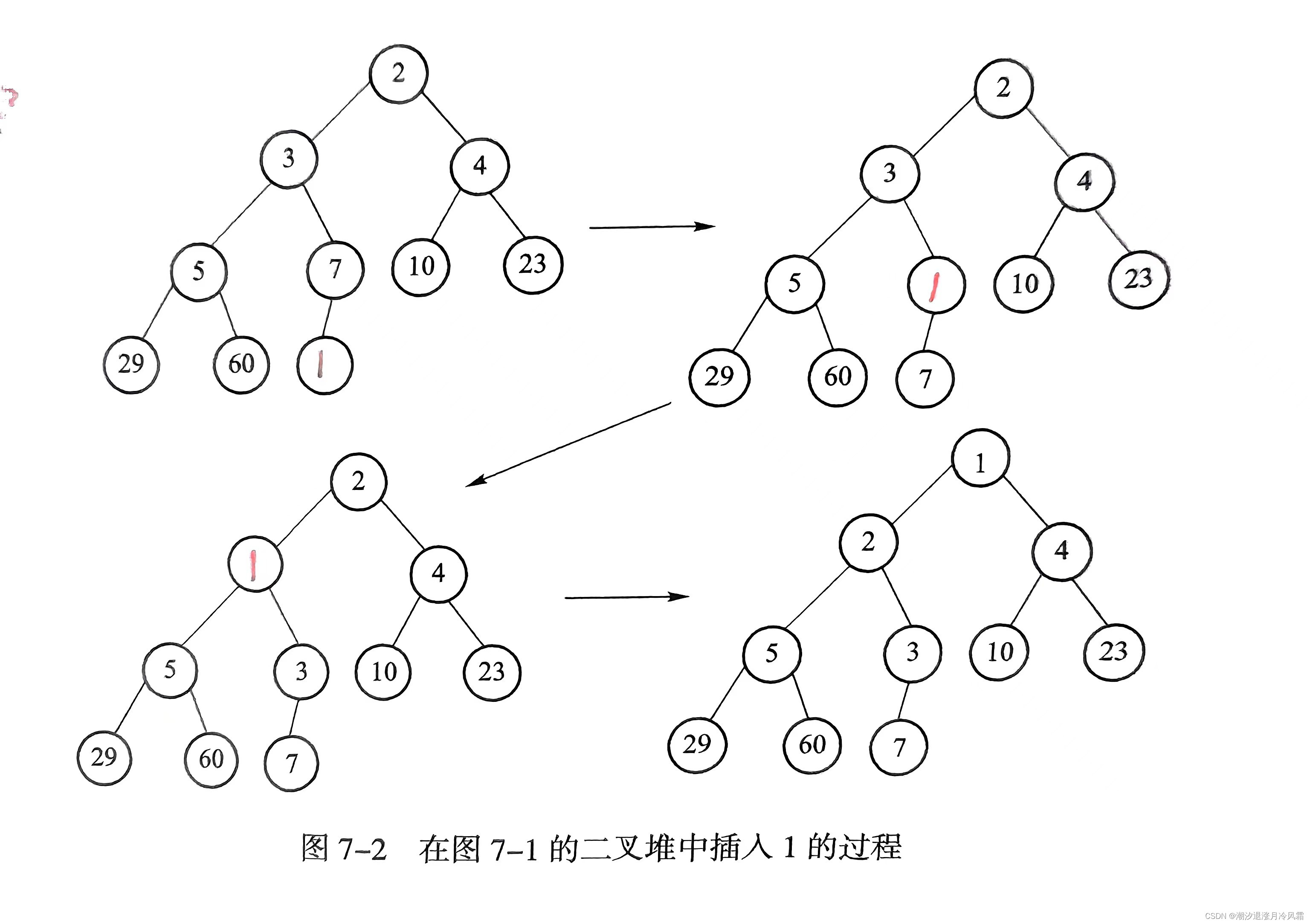
在原有的二叉堆上插入新元素,同时使其维持有序性,可以通过“上滤”实现。第一步是寻找新元素应插入的位置,第二步是插入新元素,时间复杂度为O(logn)
//先将新元素放在二叉堆最底部 int hole=++currentlength; //与父结点比较,决定是否交换(实际上不需要交换,因为新元素不一定到达最终插入位置),条件:比父结点值小,上滤过程持续进行,设置循环; //循环结束条件:到达堆顶(hole=1)或已到达最终插入位置 while(hole>1&&x<array[hole/2]) {array[hole]=array[hole/2]; //父结点下移hole/=2; //更新新元素位置 } //插入元素 array[hole]=x;
2.2 出队:下滤删除
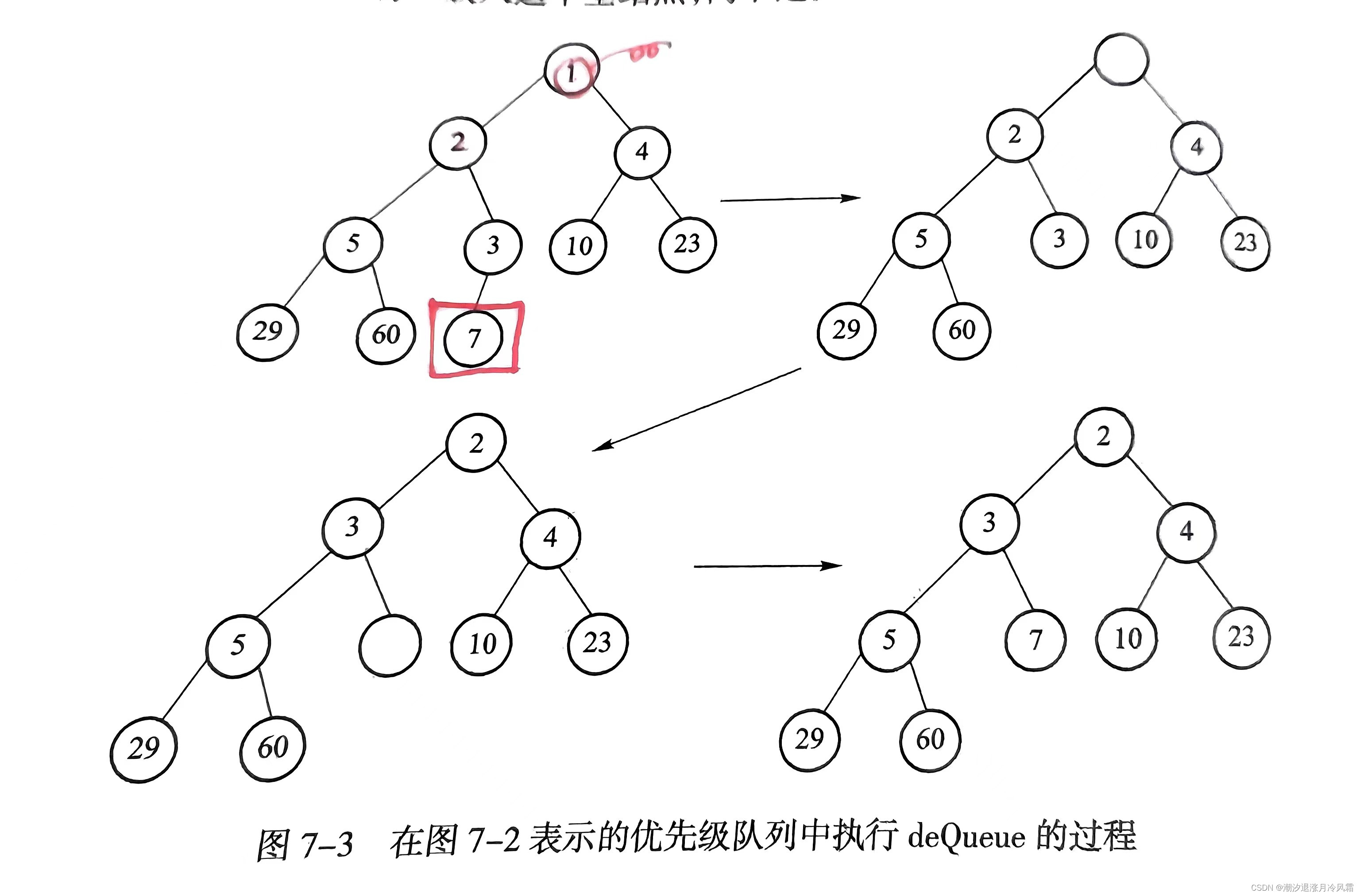
现在要删除队头元素,也就是堆顶元素,简单的想法是和孩子节点比较,选择其中较小的上滤,可这样可能会破坏二叉堆完全二叉树的结构[比如1 3 2 4 5删除后2 3 null 45],为了维持完全二叉树的结构,我们需要考虑为堆最后一个结点重新寻找位置。如图所示,将最后一个节点放在堆顶再下滤,就能实现删除堆顶元素并使二叉树结点数量减一。[比如1 3 2 4 5->
5 3 2 4->2 3 5 4],时间复杂度为O(logn)
//把最后一个元素放在堆顶 tmp=array[1]=array[currentlength--]; hole=1; //叶子结点条件 2i>n,非叶子结点条件:2i<=n while(2*hole<=currentlength){//选择较小子节点child=2*hole;if(2*hole!=currentlength) if(array[child]>array[child+1]) child++;//下滤if(tmp>array[child]) {array[hole]=array[child];hole=child;}//否则下滤结束elsebreak; //否则选择左孩子结点上滤 }
2.3 建堆
在构造函数中传入数据数组初始化二叉堆,最简单的想法是对N个元素执行N次入队操作,每次入队后对维持二叉堆有序性,时间复杂度O(nlogn);如何提升时间效率呢,可以先用原始数据初始化二叉堆,再从最后一个非叶节点开始到第一个结点,依次执行下滤操作,这样调用percolateDown(i)时保证结点i的所有自堆都满足有序性,这样自下往上,从局部有序最后抵达全局有序,可以证明这种建堆方式时间复杂度为O(n)。
对2.2中的代码略微修改容易得到下滤函数:
//下滤函数 precolateDown实现 tmp=array[i]; hole=i; while(2*hole<=currentlength){child=2*hole;if(2*hole!=currentlength) if(array[child]>array[child+1]) child++;if(tmp>array[child]) {array[hole]=array[child];hole=child;}elsebreak;建堆过程可以表示为
//建堆 buildHeap 实现 for(int i=currentlength/2;i>0;i--){precolateDown(i); }
三、 STL中的优先级队列
类模板名:priority_queue
头文件:queue
定义:priority<elemtype,base container(默认 vector),(默认大顶堆,添加谓词greater<int>则定义小顶堆)>
成员函数:
void push() 入队
void pop() 出队
Elemtype top() 获取队头元素
void clear() 清空
bool empty() 判空
四、D堆
D堆就是D叉树,由于生成的堆更矮,入队的时间复杂度为
,比二叉堆更加优越。
但出队时就不一样了,由于需要比较子结点,若采用最简单的选择算法,则时间复杂度为
,因此D堆适用于插入操作比删除操作多非常多的场景。
五、归并优先级队列(了解)
归并:即合并两棵有序树,在前面我们做过合并二叉树的题目,归并可通过递归实现
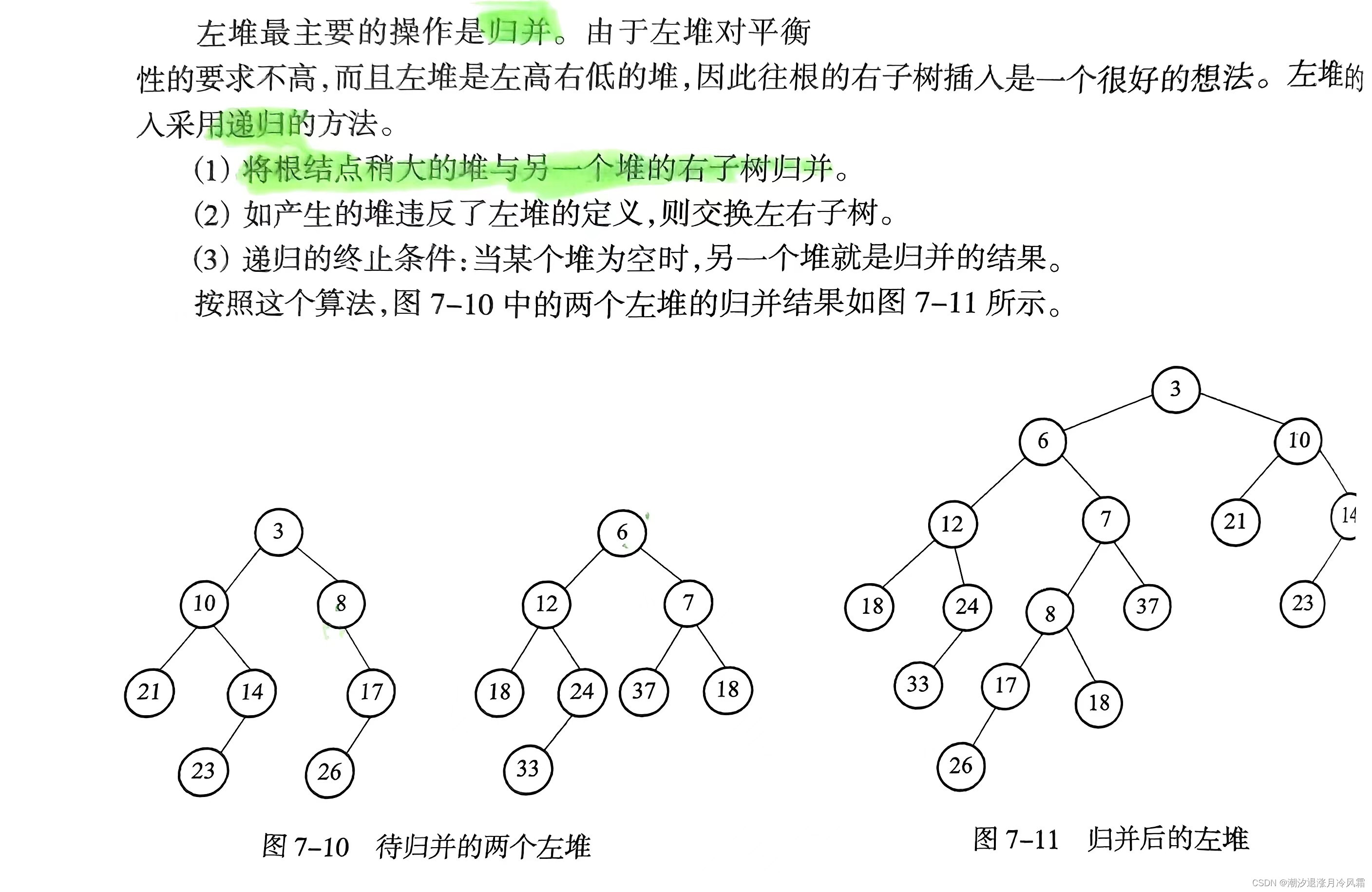
5.1 左堆
这里的nql容易通过递归实现,参考二叉树中刷题中的类似题目。

5.2 斜堆

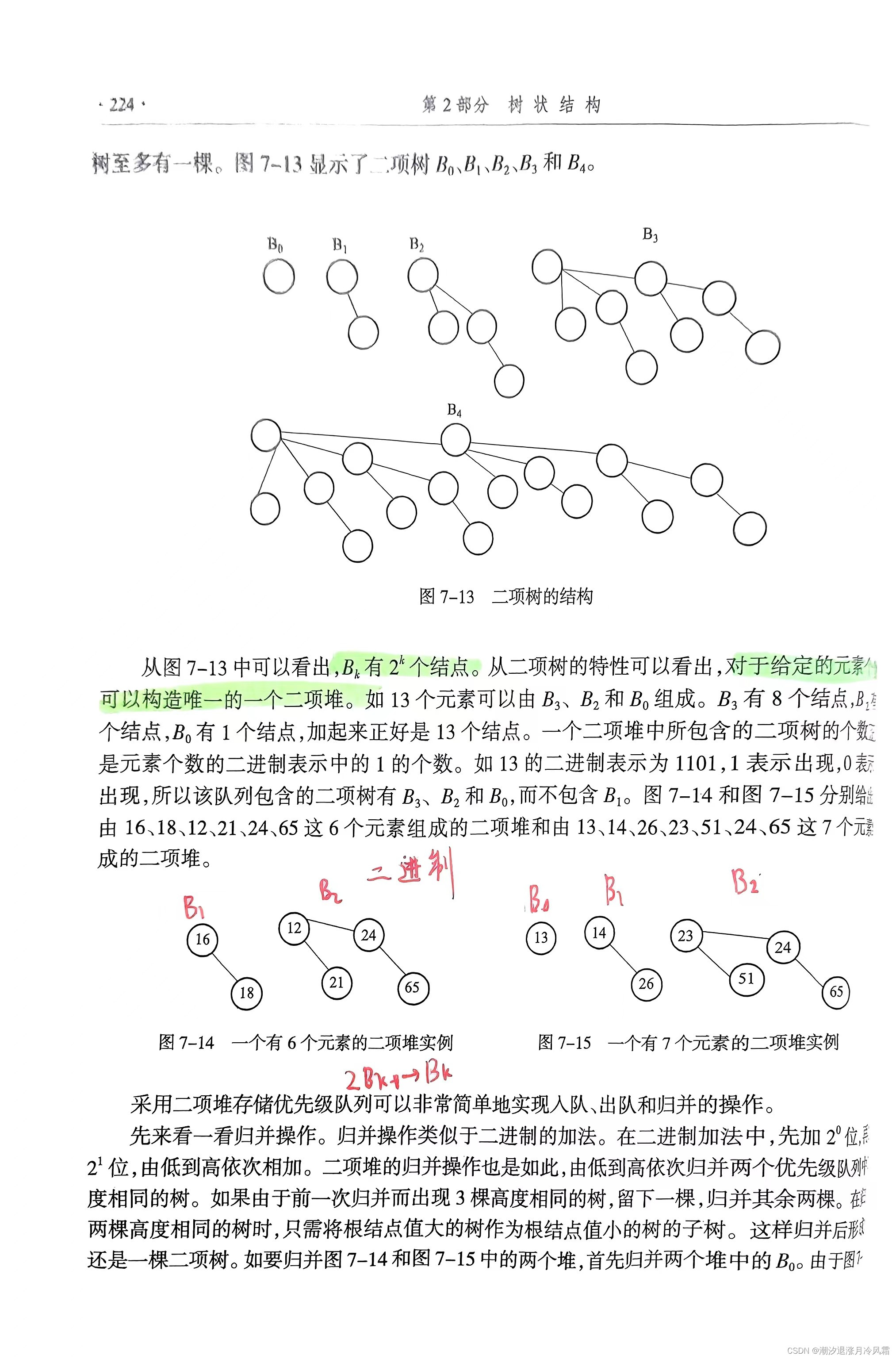
5.3 二项堆
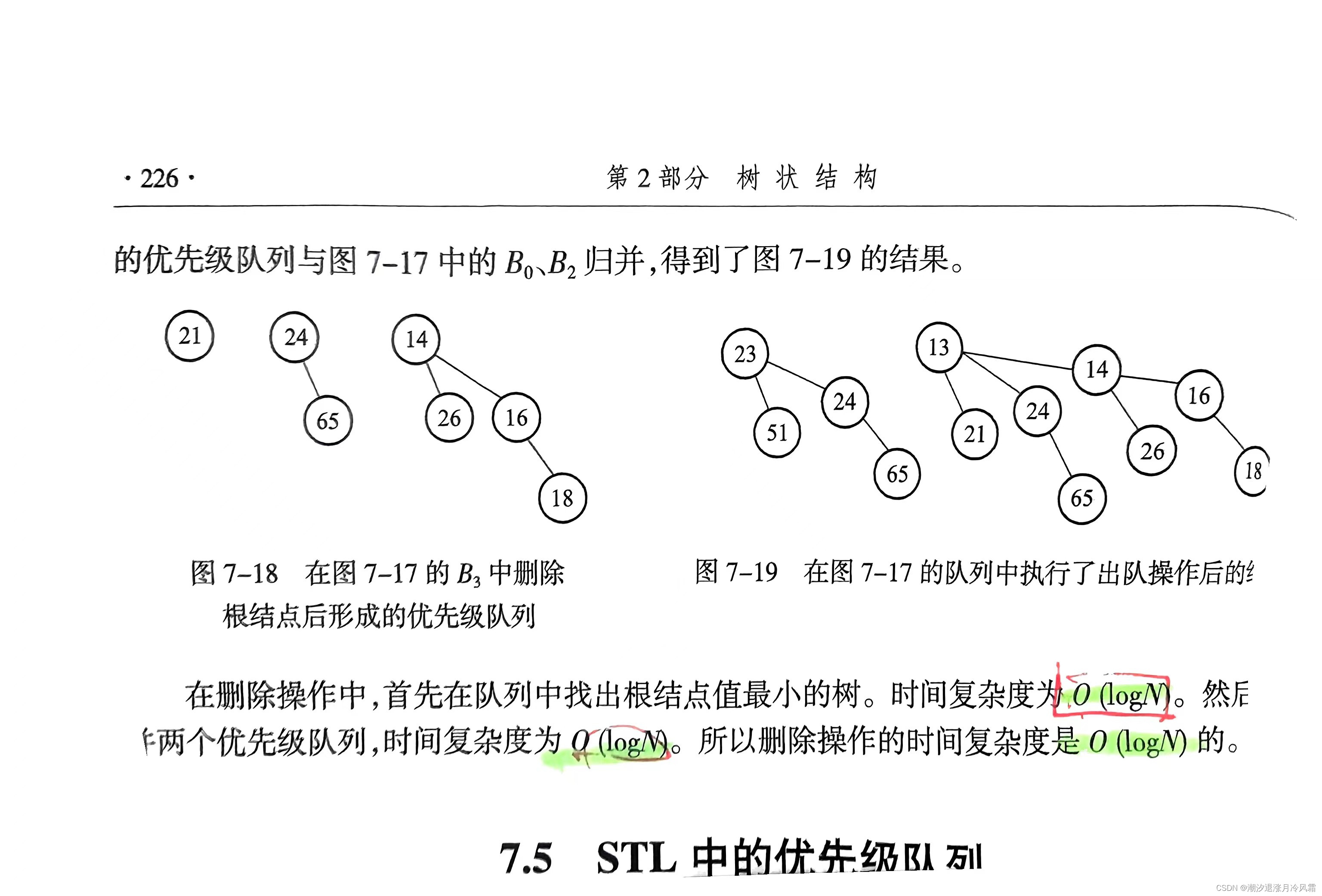
二项堆和二进制有很大相似性,归并的过程也像二进制加法