已知先序和中序序列

1. 根据先序序列找到树根
2. 根据树根和中序序列找到左右子树

同理根据后序序列和中序序列也能重构树，但前序和后序不可以

递归coding思路

设先序序列为preorder[n]，中序序列为midorder[n]

1. 大事化小：
   • 确定根，即树根为preorder[0]，左子树为preorder[1~ pos]，右子树为preorder[pos+1~ n]
   • 找到根，即查询到根在中序序列中的位置为pos，有midorder[0~ (pos-1)]是左子树，midorder[ (pos+1)~n]是右子树
2. 最小问题：子树序列长度为0——>表明是空树

例题

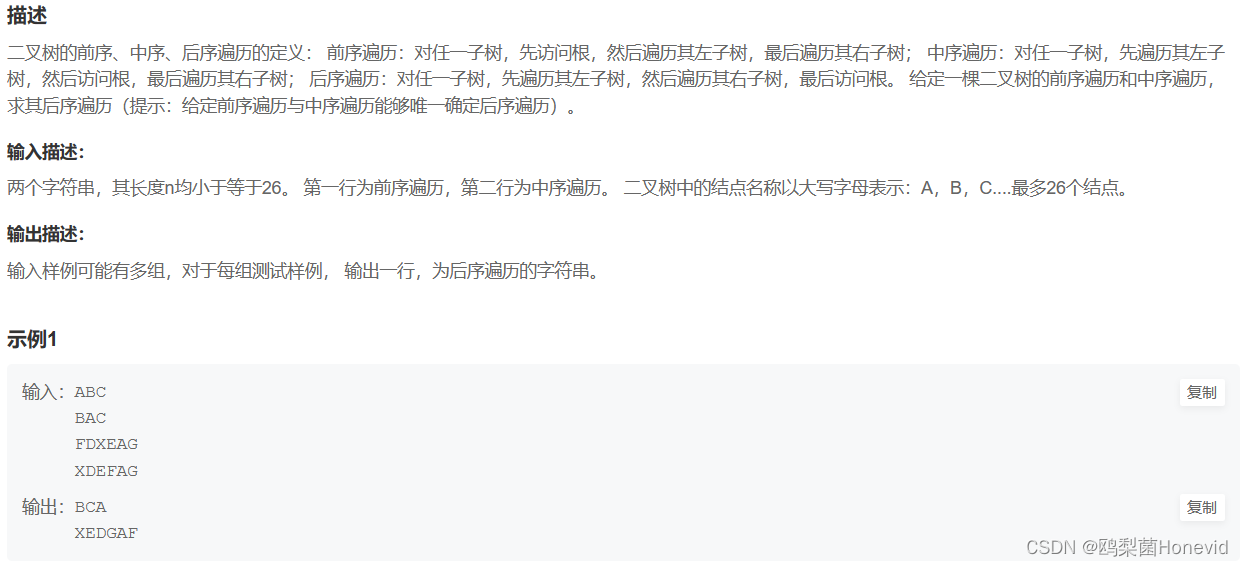
代码

#include <cstdio>
#include <string>
#include <map>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
using namespace std;struct TreeNode{char data;TreeNode * leftChild;TreeNode * rightChild;
};
struct QueueNode{TreeNode *parent;bool isLeftIn;
};void aftOrder(TreeNode* root){if (root==NULL){return;}aftOrder(root->leftChild);aftOrder(root->rightChild);printf("%c",root->data);
}
TreeNode * rebuild(string preOrder,string midOrder){//rebuild返回根节点地址if (preOrder.size()==0){return NULL;} else{//根据先序序列确定根char root_data = preOrder[0];TreeNode *new_node = new TreeNode;new_node->data = root_data;//用根切割中序序列int pos = midOrder.find(root_data);string left_pre = preOrder.substr(1,pos);//对先序序列切割，取从下标1开始，长度为pos的左子树串string right_pre= preOrder.substr(pos+1);//对先序序列切割，取右子树序列（先序）string left_mid = midOrder.substr(0,pos);string right_mid= midOrder.substr(pos+1);new_node->leftChild = rebuild(left_pre,left_mid);new_node->rightChild = rebuild(right_pre,right_mid);return new_node;}
}int main() {char preOrder[100];char midOrder[100];while(scanf("%s%s",preOrder,midOrder)!=EOF){TreeNode * root = rebuild(preOrder,midOrder);aftOrder(root);printf("\n");}return 0;
}

已知带空树提醒的先序序列

输入一个字符串，即树的先序序列，空叶部分用#填补。

递归coding思路

1. 大事化小：
   • 读取第一个非#字符：树的根
   • 接下来的非#字符：左子树根
   • 再接下来的非#字符：右子树根
2. 最小问题：读取到#，表明是空树，需要往回走了

代码

#include <cstdio>
#include <string>
#include <map>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
using namespace std;struct TreeNode{char data;TreeNode * leftChild;TreeNode * rightChild;
};
struct QueueNode{TreeNode *parent;bool isLeftIn;
};void midOrder(TreeNode* root){if (root==NULL){return;}midOrder(root->leftChild);printf("%c ",root->data);midOrder(root->rightChild);
}TreeNode * rebuild(string preOrder,string midOrder){//rebuild返回根节点地址if (preOrder.size()==0){return NULL;} else{//根据先序序列确定根char root_data = preOrder[0];TreeNode *new_node = new TreeNode;new_node->data = root_data;//用根切割中序序列int pos = midOrder.find(root_data);string left_pre = preOrder.substr(1,pos);//对先序序列切割，取从下标1开始，长度为pos的左子树串string right_pre= preOrder.substr(pos+1);//对先序序列切割，取右子树序列（先序）string left_mid = midOrder.substr(0,pos);string right_mid= midOrder.substr(pos+1);new_node->leftChild = rebuild(left_pre,left_mid);new_node->rightChild = rebuild(right_pre,right_mid);return new_node;}
}TreeNode * pre_build(int &i,string attached_preorder){char c = attached_preorder[i];++i;if (c =='#'){return NULL;} else{TreeNode * new_node = new TreeNode;new_node->data = c;new_node->leftChild = pre_build(i,attached_preorder);new_node->rightChild = pre_build(i,attached_preorder);return new_node;}
}int main() {char str[1000];scanf("%s",str);int i = 0;TreeNode * root = pre_build(i,str);midOrder(root);return 0;
}