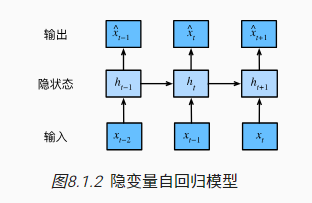
自回归模型

• 自回归模型： 只与x 有关 ，对自己执行回归
• 隐变量自回归：与X 和过去观测总结h 都有关
  

案例

%matplotlib inline
import torch
from torch import nn
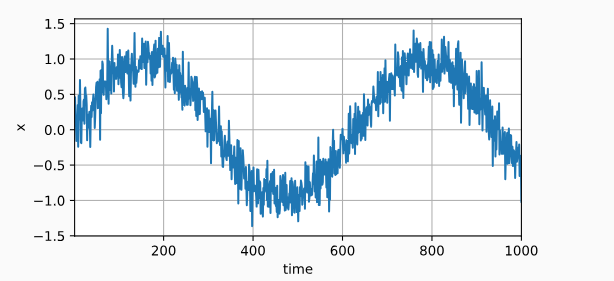
from d2l import torch as d2lT = 1000  # 总共产生1000个点
time = torch.arange(1, T + 1, dtype=torch.float32)
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))

我们将这个序列转换为模型的特征－标签（feature-label）对

tau = 4
features = torch.zeros((T - tau, tau))
for i in range(tau):features[:, i] = x[i: T - tau + i]
labels = x[tau:].reshape((-1, 1))batch_size, n_train = 16, 600
# 只有前n_train个样本用于训练
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),batch_size, is_train=True)

# 初始化网络权重的函数
def init_weights(m):if type(m) == nn.Linear:nn.init.xavier_uniform_(m.weight)# 一个简单的多层感知机
def get_net():net = nn.Sequential(nn.Linear(4, 10),nn.ReLU(),nn.Linear(10, 1))net.apply(init_weights)return net# 平方损失。注意：MSELoss计算平方误差时不带系数1/2
loss = nn.MSELoss(reduction='none')

def train(net, train_iter, loss, epochs, lr):trainer = torch.optim.Adam(net.parameters(), lr)for epoch in range(epochs):for X, y in train_iter:trainer.zero_grad()l = loss(net(X), y)l.sum().backward()trainer.step()print(f'epoch {epoch + 1}, 'f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')net = get_net()
train(net, train_iter, loss, 5, 0.01)

预测：

onestep_preds = net(features)
d2l.plot([time, time[tau:]],[x.detach().numpy(), onestep_preds.detach().numpy()], 'time','x', legend=['data', '1-step preds'], xlim=[1, 1000],figsize=(6, 3))

小结