机器学习基础08-回归算法矩阵分析（基于波士顿房价（Boston House Price）数据集）-编程知识

机器学习基础08-回归算法矩阵分析（基于波士顿房价（Boston House Price）数据集）

回归算法通常涉及到使用矩阵来表示数据和模型参数。线性回归是最常见的回归算法之一，它可以用矩阵形式来表示。

考虑一个简单的线性回归模型： $y = m x + b$ ，其中 $y$ 是因变量， $x$ 是自变量， $m$ 是斜率， $b$ 是截距。将这个模型表示成矩阵形式，可以如下所示：

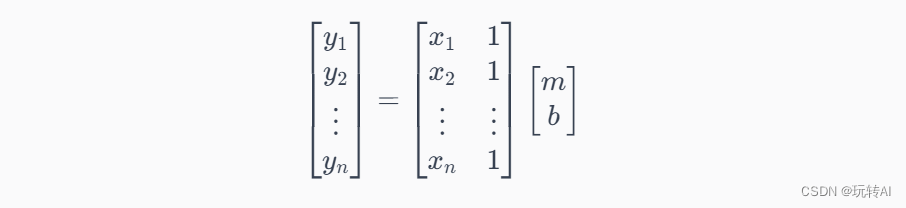
在这里插入图片描述
在上面的矩阵表达中，左边的矩阵表示因变量 $y$ ，右边的矩阵表示自变量 $x$ 和一个常数项 $1$ 。而模型参数 $m$ 和 $b$ 则以矩阵的形式表示。

通过最小化残差（观测值与模型预测值之间的差异）来确定最佳的参数 $m$ 和 $b$ ，这通常涉及到矩阵计算中的求解方法，如最小二乘法。

其他更复杂的回归算法，例如多变量线性回归、岭回归、Lasso回归等，也可以通过矩阵表示来进行推导和求解。矩阵表示使得回归算法的计算更加紧凑和易于理解。

接下来将介绍三种评估机器学习的回归算法的评估矩阵。

平均绝对误差（Mean Absolute Error，MAE）。
均方误差（Mean Squared Error，MSE）。
决定系数（R2）。

示例中采用将使用波士顿房价（Boston House Price）数据集进行实验操作

数据集下载地址

https://github.com/selva86/datasets/blob/master/BostonHousing.csv

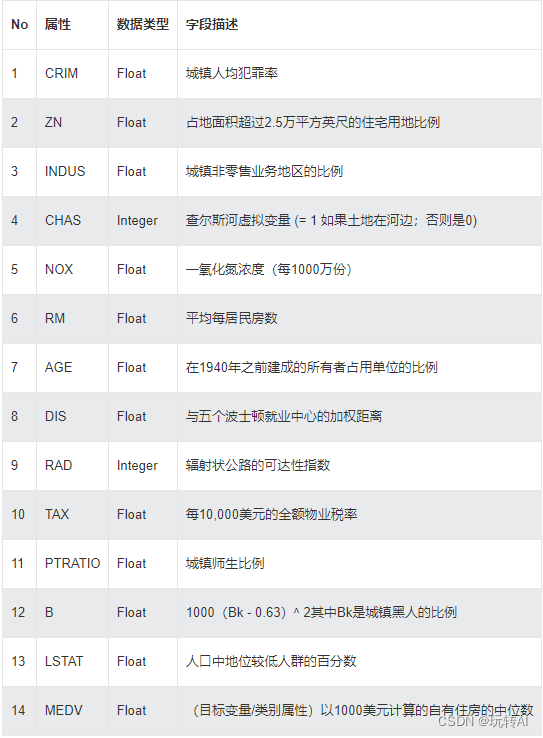
数据集介绍：

波士顿房价预测更像是预测一个连续值，当然这也是一个非常经典的机器学习案例
在这里插入图片描述

平均绝对误差

平均绝对误差是所有单个观测值与算术平均值的偏差的绝对值的平均值。与平均误差相比，平均绝对误差由于离差被绝对值化，不会出现正负相抵消的情况，因而，平均绝对误差能更好地反映预测值误差的实际情况。

代码如下：


import pandas as pd
from sklearn.linear_model import  LinearRegressionfrom sklearn.model_selection import  KFold, cross_val_score#数据预处理
path = 'D:\down\\BostonHousing.csv'
data = pd.read_csv(path)array = data.valuesX = array[:, 0:13]
Y = array[:, 13]n_splits = 10seed = 7kflod = KFold(n_splits=n_splits, random_state=seed, shuffle=True)
#
model = LinearRegression()scoring = 'neg_mean_absolute_error'results = cross_val_score(model, X, Y, cv=kflod, scoring=scoring)print("MSE: %.3f (%.3f)" % (results.mean(), results.std()))

执行结果如下：


MSE: -3.387 (0.667)

均方误差

均方误差是衡量平均误差的方法，可以评价数据的变化程度。均方根误差是均方误差的算术平方根。均方误差的值越小，说明用该预测模型描述实验数据的准确度越高。

代码如下：


import pandas as pd
from sklearn.linear_model import  LinearRegressionfrom sklearn.model_selection import  KFold, cross_val_score#数据预处理
path = 'D:\down\\BostonHousing.csv'
data = pd.read_csv(path)array = data.valuesX = array[:, 0:13]
Y = array[:, 13]n_splits = 10seed = 7kflod = KFold(n_splits=n_splits, random_state=seed, shuffle=True)
#
model = LinearRegression()scoring = 'neg_mean_squared_error'results = cross_val_score(model, X, Y, cv=kflod, scoring=scoring)print("MSE: %.3f (%.3f)" % (results.mean(), results.std()))

运行结果如下：

MSE: -23.747 (11.143)

决定系数（R2）

决定系数，反映因变量的全部变异能通过回归关系被自变量解释的比例。拟合优度越大，自变量对因变量的解释程度越高，自变量引起的变动占总变动的百分比越高，观察点在回归直线附近越密集。

如R2为0.8，则表示回归关系可以解释因变量80%的变异。换句话说，如果我们能控制自变量不变，则因变量的变异程度会减少80%。
决定系数（R2）的特点：

可决系数是非负的统计量。
可决系数的取值范围：0≤R2≤1。
可决系数是样本观测值的函数，是因随机抽样而变动的随机变量。为
此，对可决系数的统计的可靠性也应进行检验。

代码如下：


import pandas as pd
from sklearn.linear_model import  LinearRegressionfrom sklearn.model_selection import  KFold, cross_val_score#数据预处理
path = 'D:\down\\BostonHousing.csv'
data = pd.read_csv(path)array = data.valuesX = array[:, 0:13]
Y = array[:, 13]n_splits = 10seed = 7kflod = KFold(n_splits=n_splits, random_state=seed, shuffle=True)
#
model = LinearRegression()scoring = 'r2'results = cross_val_score(model, X, Y, cv=kflod, scoring=scoring)print("R2: %.3f (%.3f)" % (results.mean(), results.std()))

执行结果如下：