进阶了解C++(6)——二叉树OJ题-编程知识

Leetcode.606.根据二叉树创建字符串：

606. 根据二叉树创建字符串 - 力扣（LeetCode）

难度不大，根据题目的描述，首先对二叉树进行一次前序遍历，即：

class Solution {
public:string tree2str(TreeNode* root) {if(root == nullptr){return "";}string ret = to_string(root->val);ret += tree2str(root->left);ret += tree2str(root->right);return ret;}
};

输出结果如下：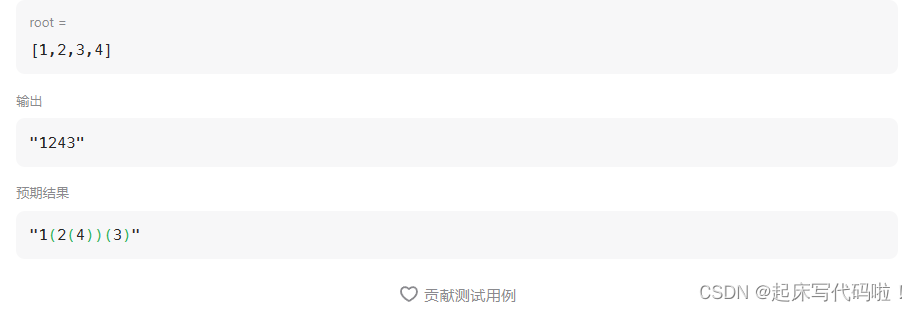

从结果看到，元素输出的顺序正确，但是输出的格式不正确。对于题目要求的格式输出，不难发现，当一个结点的左子树的结点为空时，括号不输出。当一个结点的左子树的结点为空，但是右子树的结点不为空时，正常打印左，右结点的括号。只有当右结点存在时，才打印右结点的括号。

1.结点的左子树结点为空，但是结点的右子树结点不为空，此时正常对结点的左子树结点的括号进行打印。

2.结点的左子树结点为空，同时右子树结点为空，此时不打印任何括号。

因此，对于上面两种结点情况的判定，可以使用 $\left | \right |$ 逻辑完成。首先判断 $root->left$ 是否为空，如果不为空，则正常打印左结点的括号。如果为空，则去判断 $root->right$ ，如果不为空，则正常打印左结点的括号，如果为空，则不打印左结点的括号。

对于右结点情况的判定，如果右结点为空，则不打印括号，如果不为空，则正常打印，因此，对应代码如下：

class Solution {
public:string tree2str(TreeNode* root) {if(root == nullptr){return "";}string ret = to_string(root->val);if(root->left || root->right){ret+='(';ret += tree2str(root->left);ret+=')';}if(root->right){ret+='(';ret += tree2str(root->right);ret+=')';}return ret;}
};

运行结果如下：

Leetcode.102 二叉树的层序遍历：

102. 二叉树的层序遍历 - 力扣（LeetCode）

对于本题，可以利用队列来实现，具体思路如下：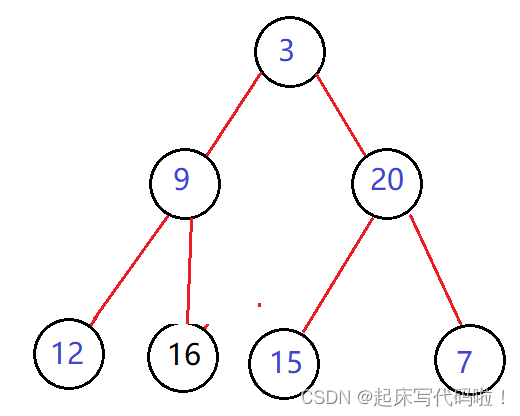

首先利用栈，将二叉树根结点所对应的元素压入队列，即：

由于层序遍历的特点，因此在下一步，需要将 $3$ 的左右子树的结点 $9,20$ 进入队列。不过此时会面临一个问题，如何判断下一层全部进入队列？对于图中的树，第二层只有两个结点，姑且可以人为创建两次入队列的操作，但是对于下面层的结点，例如结点的数量为 $x$ 个，不好判断入队列的次数。但是，对于这 $x$ 个结点，因为其父结点的原因。是绝对可以在 $x/2$ 次数内入完队列的。所以，对于入队列的次数，可以分成 $x/2$ 次数次完成，即通过其父结点来完成。

所以，额外定义一个变量 $levelsize$ 来记录本层结点，即下一层结点的父结点的数量，例如对于上图中的队列， $levelsize=1$ 。

随后，利用循环，循环 $levlesize$ 次，保证子结点都能入到队列中。由于题目要求的输出方式是类似于二维数组的方式，所以需要额外创建一个 $vector<int>$ 类型的变量 $v$ 用于向二维数组中不断插入层序遍历到的结点。

对于上述步骤，仅仅用文字描写不够清晰，下面将利用图片进行演示：
首先，层序遍历每一层的结点的结果在输出时是独立的，因此，在进入循环后，首先创建一个指针 $front$ 将 $queue$ 中的结点的地址进行保存，并且将这个结点出队列。即：

然后，将这个结点的数值插入到 $v$ 中，即：

随后，让 $front$ 的左右结点依次入队列，即：

随后，令 $v$ 插入到二维数组 $vv$ 中，并且由于此时队列中存储了两个结点，所以改变 $levelsize$ ，即：

至此，一次循环运行完毕。由于第一层的 $levelsize==1$ ，因此上述步骤只会进行一次。为了便于理解，再给出第二次循环的相关图片解释。

此时队列中存储了 $9,20$ 两个结点的地址。首先利用 $front$ 结点保存队列中第一个结点的地址。即：

然后让队列头部元素出队列，并且将这个元素插入到 $v$ 中，即：

随后，让 $front$ 的左右结点依次进队列，即：

由于 $levelsize==2$ ，因此，上述步骤还会进行一次，第二次具体如下：
利用 $front$ 保存队列的头部元素，然后出队列的头部元素，再令 $v$ 保存 $front->val$ 即：

然后在令 $front$ 左右结点的地址进入队列，即：

最后，令 $vv$ 保存 $v$ ，再改变 $levelsize$ ，即：

对应代码如下：

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> vv;//用于进出每一次的结点queue<TreeNode*> q;//记录每层结点数量int levelsize = 0;if(root){q.push(root);levelsize = 1;}while(!q.empty()){vector<int> v;while(levelsize--){TreeNode* front = q.front();q.pop();v.push_back(front->val);if(front->left)q.push(front->left);if(front->right)q.push(front->right);}levelsize = q.size();vv.push_back(v);}return vv;}
};

在上面的代码中，需要注意，由于 $v$ 保存的是某一层的结点，与上层无关，因此， $v$ 定义在第一层 $while$ 循环中，可以保证，每次循环执行完毕后， $v$ 都会进行一次自动的更新。

运行结果如下：

Leetcode.236 二叉树的最近公共祖先：

236. 二叉树的最近公共祖先 - 力扣（LeetCode）

本题可以说是本文中难度最大题目。对于题目中公共祖先的定义，可以分为下面的类型：
例如对于下面给出的二叉树中，结点 $7,0$ 的最近公共祖先为根结点，即存储值为 $3$ 的结点：

对于结点 $6,4$ 的最近公共祖先为存储值为 $5$ 的结点，即：

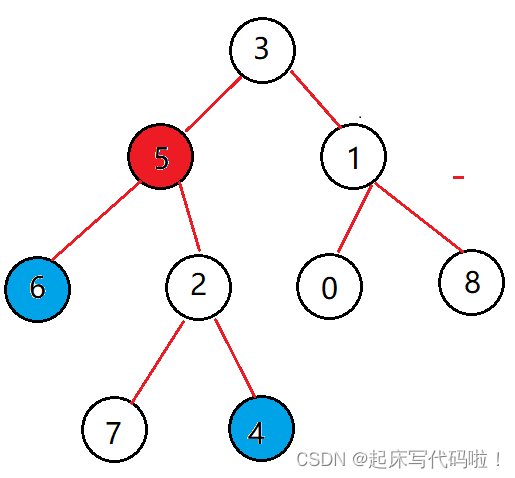
对于结点 $2,4$ 的最近公共祖先是存储值为 $2$ 的结点，即：

通过对于上面不同结点所对应的公共结点，可以得到寻找公共结点的规律：

1.如果给定的两个结点 $p,q$ 分别在树的左子树和右子树，则根结点 $root$ 就是最近公共结点。(对应第一个图所对应的情况)。

2.如果给定的两个结点 $p,q$ 同时在树的左子树或者同时在树的右子树，(对应第二个图所对应的情况),此时，可以去判断 $p,q$ 是否在根结点的子结点的左右，如果在，则根结点的子结点就是 $p,q$ 的最近公共祖先，即：

3.如果 $p,q$ 中的一个是另一个的子结点，例如假设 $p$ 是 $q$ 的子结点，则 $q$ 就是最近公共结点。

因此，在查找 $p,q$ 的最近公共祖先之前，需要先确定 $p,q$ 两个结点在树中的位置。二者的位置可以分为下面四种情况： $p$ 结点在左子树， $p$ 结点在右子树， $q$ 结点在左子树， $q$ 结点在右子树。为了方便表示，用 $pInleft,pInright,qInleft,qInright$ 分别表示上面的四种情况。对于上面结点位置的查询，可以使用递归来实现，具体代码如下：

bool IsInTree(TreeNode* root, TreeNode* x){if(root == nullptr){return false;}return root == x || IsInTree(root->left,x) || IsInTree(root->right,x);}

同时，如果题目给定的树为空树，则不需要进行判断，如果给定的 $p,q$ 其中之一就是根结点，则直接返回根结点即可。

在利用上面的代码确定了 $p,q$ 结点在树中的位置后，需要分下面的情况进行判定：
入如果 $pInleft,qInright$ 同时为真或者 $pInright,qInleft$ 同时为真，则说明 $p,q$ 结点分别分布在左子树或者右子树。因此对于这种情况，直接返回根结点即可。

如果 $pInleft,qInleft$ 同时为真或者 $pInright,qInright$ 同时为真，则说明 $p,q$ 同时在左子树或者右子树。因此直接对其根结点左子树，或者右子树进行重复判断即可。对应代码如下：

class Solution {
public:bool IsInTree(TreeNode* root, TreeNode* x){if(root == nullptr){return false;}return root == x || IsInTree(root->left,x) || IsInTree(root->right,x);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == nullptr){return nullptr;}if(root == p || root == q){return root;}bool pInleft,pInright,qInleft,qInright;pInleft = IsInTree(root->left,p);pInright = ! pInleft;qInleft = IsInTree(root->left,q);qInright = ! qInleft;if((pInleft && qInright) || (pInright && qInleft)){return root;}else if((pInleft && qInleft) ){return lowestCommonAncestor(root->left,p,q);}else if((qInright && pInright)){return lowestCommonAncestor(root->right,p,q);}assert(false);return nullptr;}
};

运行结果如下：

但是这种方法时间复杂度太大。因此，可以采用下面的方法来优化时间复杂度：

例如对于上面的树，如果将查找两个结点的路径记录，则记录的结点如下：

则不难发现，所谓的最近公共祖先，就是二者路径上最近的相同结点。而重点，就是如何去记录这个路径。文章给出一种方法，具体如下：
首先将寻找路径的函数命名为 $GetPath$ ，首先检测当前结点是否为空，如果为空，则直接返回 $false$ ，如果不为空，首先创建一个栈，这里将这个栈命名为 $s$ ，让结点入栈。在入栈后，检测当前结点是否是需要寻找的结点，如果是则返回 $true$ 。如果不是，则分别递归结点的左右子树。如果在左右子树中没有找到，则出栈一次。为了方便理解，下面用图来演示这一过程：

首先，此时的结点 $3$ 不为空，因此直接入栈，即：

由于 $3$ 并不是需要找的结点，因此先去结点的左子树中进行寻找，即 $5$ 。与上方相同的逻辑，首先让 $5$ 入栈，即：

由于 $5$ 也不是需要查找的结点，因此按照递归，再去左子树进行查找。

让结点 $6$ 入栈，即：

由于 $6$ 也不是需要找的结点，因此继续往左子树递归。由于 $6$ 结点的左，右子树结点都为空，因此判定为左，右子树都找不到结点，所以将 $6$ 弹出栈，即：

此时递归回到上一层，由于 $5$ 结点的左子树找不到需要的结点，因此去其右子树进行查找，即将 $2$ 入栈；

同时，由于 $2$ 也不是需要找的结点，因此去其左子树进行查找，即将 $7$ 入栈。由于此时的结点为需要查找的结点，因此返回 $true$ 。此时栈中内容如下；

此时，便获取了查找结点的路径。

对于另一个需要查找的结点，由于原理相同，因此不再过多叙述。

在得到了两个结点的路径后，首相让长的路径逐渐 $pop$ ，直到两个栈的 $size$ 相同即可。随后挨个比较栈中元素。如果相同则返回即可。对应代码如下：

class Solution {
public:bool GetPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& s){if(root == nullptr){return false;}s.push(root);if(root == x){return true;}if(GetPath(root->left,x,s)){return true;}if(GetPath(root->right,x,s)){return true;}s.pop();return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {stack<TreeNode*> sp;stack<TreeNode*> sq;GetPath(root,p,sp);GetPath(root,q,sq);while(sp.size() != sq.size()){if(sp.size() > sq.size()){sp.pop();}else{sq.pop();}}while(sp.top() != sq.top()){sp.pop();sq.pop();}return sp.top();}
};

运行结果如下：