一、问题背景与基本设定

我们面临一个有趣的水壶配对问题：给定n个红色水壶和n个蓝色水壶，它们的形状和尺寸各不相同。每个红色水壶中的水量都是唯一的，每个蓝色水壶也是如此。重要的是，对于每个红色水壶，都存在一个蓝色水壶与之水量相等，反之亦然。我们的任务是通过一系列操作找出这些配对的水壶。

操作方式如下：选择一个红色水壶和一个蓝色水壶，将红色水壶装满水，然后倒入蓝色水壶。通过这个过程，我们可以判断红色水壶的水是多于、少于还是等于蓝色水壶的水。每次这样的比较需要消耗一个单位时间。

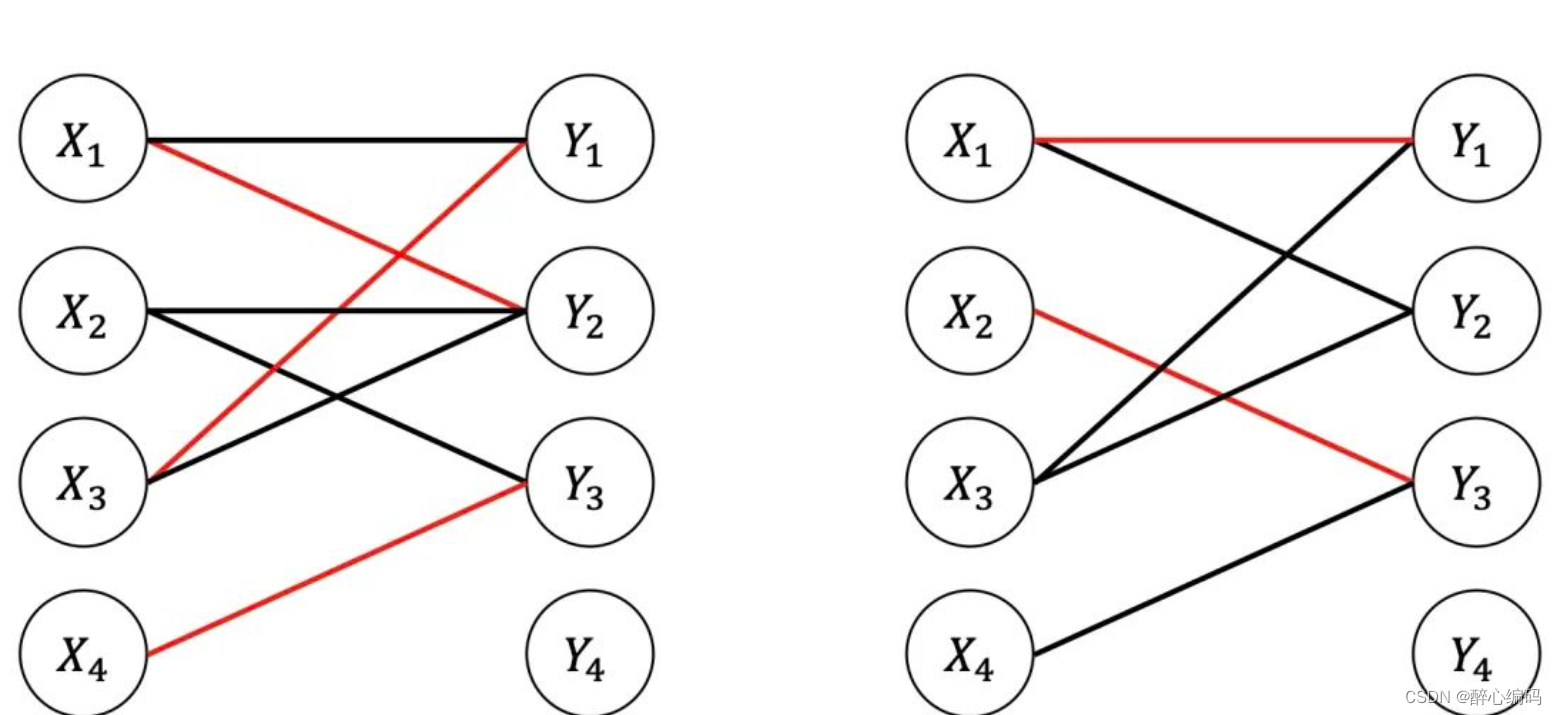
二、确定性算法设计（θ(n²)次比较）

我们可以设计一个直观的算法来解决这个问题，虽然它不是最优的，但它的复杂度是确定的θ(n²)。

算法步骤如下：

初始化一个空的配对列表。
对于每一个红色水壶Ri（i从1到n）：
对于每一个蓝色水壶Bj（j从1到n）：
比较Ri和Bj的水量。
如果水量相等，将它们添加到配对列表中，并标记为已配对。
如果不等，继续下一次比较。
返回配对列表。
这个算法的时间复杂度是θ(n²)，因为我们需要对每个红色水壶执行n次比较操作。

三、算法比较次数的下界证明（Ω(nlgn)）

为了证明解决该问题的任何算法都需要至少Ω(nlgn)次比较，我们可以采用信息论的方法。

考虑这样一个事实：存在n!种可能的水壶配对方式。每次比较最多提供给我们1比特的信息（即红色水壶的水是多于、少于还是等于蓝色水壶的水）。为了确定正确的配对方式，我们需要足够的信息来区分所有可能的配对。

所需的最少信息量可以用配对方式的熵来表示，即log₂(n!)比特。利用斯特林近似公式，我们可以得出n! ≈ √(2πn) * (n/e)ⁿ。因此，log₂(n!) ≈ nlog₂n - nlog₂e + O(logn)。

由于每次比较最多提供1比特的信息，所以至少需要nlog₂n - nlog₂e + O(logn)次比较才能确定配对。这证明了任何算法的比较次数下界为Ω(nlgn)。

四、确定性算法（θ(n²)）伪代码

function pairWaterJugs(redJugs, blueJugs):  pairs = []  for each redJug in redJugs:  for each blueJug in blueJugs:  result = compare(redJug, blueJug)  if result == "equal":  pairs.append((redJug, blueJug))  remove redJug from redJugs  remove blueJug from blueJugs  break  return pairs  function compare(jug1, jug2):  // 假设这里有一个方法可以比较两个水壶的水量  // 返回 "less", "equal", 或 "greater"

五、确定性算法C代码示例

#include <stdio.h>  
#include <stdbool.h>  typedef struct Jug {  int id; // 水壶的唯一标识符  int waterLevel; // 水壶中的水量  
} Jug;  typedef struct JugPair {  Jug redJug;  Jug blueJug;  
} JugPair;  // 假设的compare函数，仅用于示例  
int compare(Jug jug1, Jug jug2) {  if (jug1.waterLevel < jug2.waterLevel) return -1;  if (jug1.waterLevel == jug2.waterLevel) return 0;  return 1;  
}  JugPair* pairWaterJugs(Jug redJugs[], Jug blueJugs[], int n, int *pairCount) {  JugPair *pairs = malloc(n * sizeof(JugPair));  *pairCount = 0;  for (int i = 0; i < n; i++) {  for (int j = 0; j < n; j++) {  if (compare(redJugs[i], blueJugs[j]) == 0) {  pairs[*pairCount].redJug = redJugs[i];  pairs[*pairCount].blueJug = blueJugs[j];  (*pairCount)++;  break; // 假设每个红色水壶只配对一个蓝色水壶，找到后跳出内层循环  }  }  }  return pairs;  
}  // 主函数和其他辅助函数省略...

六、随机算法设计（期望比较次数O(nlgn)）

我们可以设计一个基于分治的随机算法，其期望的比较次数为O(nlgn)。

算法步骤如下：

如果只有一个红色水壶和一个蓝色水壶，直接比较它们并返回结果。
否则，随机选择一个红色水壶Ri。
使用Ri与所有蓝色水壶进行比较，找到与之水量相等的蓝色水壶Bi。这需要n次比较。
移除已配对的Ri和Bi，将剩余的水壶分为两组：一组是水量少于Ri的红色水壶和水量多于Bi的蓝色水壶，另一组是水量多于Ri的红色水壶和水量少于Bi的蓝色水壶。
递归地对这两组水壶执行步骤1到4。
由于每次递归我们都至少移除了一对水壶，所以递归的深度最多为n。在每一层递归中，我们总共进行n次比较（步骤3）。因此，总的比较次数是n乘以递归的深度，即O(n²)在最坏情况下。

然而，我们可以证明这个算法在平均情况下的期望比较次数是O(nlgn)。这是因为在每次递归中，我们都有一半的概率选择到接近中位数水量的红色水壶Ri，从而将剩余的水壶大致均匀地分成两组。这种均匀分割的情况在期望上会导致递归树的高度为O(lgn)，因此总的比较次数为O(nlgn)。

七、最坏情况下的比较次数

对于上述随机算法，最坏情况下的比较次数仍然是O(n²)。这是因为在最坏的情况下，我们可能每次都选择到最大或最小的红色水壶，导致递归树的高度为n，而不是期望的O(lgn)。然而，这种情况发生的概率是非常低的，所以期望的比较次数仍然是O(nlgn)。

八、随机算法（期望O(nlgn)）伪代码

function pairWaterJugsRandomized(redJugs, blueJugs):  if length of redJugs == 1 and length of blueJugs == 1:  if compare(redJugs[0], blueJugs[0]) == "equal":  return [(redJugs[0], blueJugs[0])]  else:  return []  pivotRed = select random jug from redJugs  pivotBlue = findMatchingBlue(pivotRed, blueJugs)  if pivotBlue is found:  lessPairs = pairWaterJugsRandomized(filter less redJugs, filter greater blueJugs)  greaterPairs = pairWaterJugsRandomized(filter greater redJugs, filter less blueJugs)  return lessPairs + [(pivotRed, pivotBlue)] + greaterPairs  else:  // No matching blue jug found, which should not happen if the problem statement holds true.  return []  function findMatchingBlue(redJug, blueJugs):  for each blueJug in blueJugs:  if compare(redJug, blueJug) == "equal":  return blueJug  return null // or some sentinel value indicating not found

九、随机算法C代码示例

// 伪代码的C语言风格概述，不是完整的C程序  
Jug findMatchingBlue(Jug redJug, Jug blueJugs[], int n) {  // 实现查找匹配蓝色水壶的逻辑...  
}  JugPair* pairWaterJugsRandomized(Jug redJugs[], Jug blueJugs[], int n, int *pairCount) {  if (n == 1) {  // 处理基本情况...  }  // 随机选择一个红色水壶...  Jug pivotRed = redJugs[rand() % n];  Jug pivotBlue = findMatchingBlue(pivotRed, blueJugs, n);  if (pivotBlue.id != -1) { // 假设-1表示未找到  // 递归处理小于和大于pivotRed的水壶...  }  // 返回配对结果...  
}

十、结论

我们设计了一个确定性算法来解决水壶配对问题，其时间复杂度为θ(n²)。我们还证明了任何解决该问题的算法的比较次数下界为Ω(nlgn)。最后，我们设计了一个随机算法，其期望的比较次数为O(nlgn)，但在最坏情况下的比较次数可能达到O(n²)。这个随机算法在实际应用中可能更为有效，因为它在平均情况下提供了更好的性能。