C语言数据结构基础——排序-编程知识

1.插入排序

2.冒泡排序

3. 堆排序

4.希尔排序

5.直接选择排序

6.快速排序☆☆

6.1快速排序基础

6.2关于快速排序的时间复杂度

6.3随机数法和三数取中法

6.4其他的单趟实现方法

6.4.1挖坑法

6.4.2前后指针版快速排序☆

6.4.3非递归实现快排☆

7.归并排序

7.1递归实现

7.2非递归实现

8.计数排序

9.小结

1.插入排序

把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为 止，得到一个新的有序序列 。我们玩扑克牌整理牌时就是插入排序。

先写单趟，再写总体。

单趟：

end作为下标，始终指向未比较数据的最后一个数据，若发现tmp还是小于end的值，就让end的数据向数组正向覆盖，并且--end，再重复上述比较来判断是否可以把tmp放在现在end+1的位置上。另外，若最后end都变成-1了，说明此前tmp一直小于end，直接跳出循环并将tmp放在end+1(也就是0的位置上)

用tmp记录我们希望插入的数据，并永远放在end+1的位置处

整体：

我们认为下标为0（第一个数据）是有序的。

直接改成end从小到大的双层循环即可。

void InsertSort(int* arr, int number) {for (int i = 1; i < number; i++) {int tmp = arr[i];for (int end = i-1; end >= 0; end--) {if (tmp < arr[end]) {arr[end + 1] = arr[end];}else {arr[end + 1] = tmp;break;}}}}void InsertSort(int* arr, int number) {for (int i = 1; i < number; i++) {int tmp = arr[i];int end = i - 1;for (int end = i-1; end >= 0; end--) {if (tmp < arr[end]) {arr[end + 1] = arr[end];}else {break;}}arr[end + 1] = tmp;}}void InsertSort(int* arr, int number) {for (int i = 1; i < number; i++) {int tmp = arr[i];int end = i - 1;for (; end >= 0; end--) {if (tmp < arr[end]) {arr[end + 1] = arr[end];}else {break;}}arr[end + 1] = tmp;}}

好好反思，易错辨析：只有最后一段代码是对的，你看出前两种有错了吗？

对于第一段代码，无法处理end减到-1之后的情况

对于第二段代码，在for循环中重新定义了end变量，因此第二层for循环的end与出循环之后的end不是同一个end，局部变量的使用优先级更高。

对于插入排序，最坏情况时，移动次数就是等差数列之和（整个数组逆序），第二个数据挪一个，第三个数据挪两个

............

等差数列求和的最大项就是n^2

对于最好的情况：至少要遍历一遍才能知道其都是顺序，所以最好的情况都是O(N)

tips：没有排序能o(1)，最好的情况都是O(N),最坏情况的最优效率都是O(nlogn)

2.冒泡排序

每一轮都能将暂且最大的数字冒的最后

如果某一圈一个都没有冒过，说明已经有序了，可以直接跳出循环。

稍加控制条件即可。

时间复杂度 O(N^2)
最好情况：顺序有序或者接近有序， O(N)（至少都要遍历一次才知道该数组是否有序，再次印证了没有排序能做到O(1）

在开始新的排序之前，我们测试一下冒泡和插入的效率。

测试性能时请用realse版本，不要用debug,debug的优化不够，不能凸显差异。

提供给大家一个测试函数，包含了之后会使用到的排序函数

创建了大量数据随机数并且放入数组，使用clock函数计数每一种排序的具体时间。

void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();//InsertSort(a1, N);int end1 = clock();int begin7 = clock();//BubbleSort(a7, N);int end7 = clock();int begin2 = clock();//ShellSort(a2, N);int end2 = clock();int begin3 = clock();//SelectSort(a3, N);int end3 = clock();int begin4 = clock();//HeapSort(a4, N);int end4 = clock();int begin5 = clock();//QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();//MergeSort(a6, N);int end6 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("BubbleSort:%d\n", end7 - begin7);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}

先对写好的冒泡和插入进行比较：

尽管时间复杂度都是一样的，但是具体消耗时间确相差很大。

尽管可以认为他们两个是同样的量级（相同的时间复杂度）

可是，插入为什么优于冒泡这么多？

尽管两种算法的最坏时间复杂度是一样的，

但是插入排序的“适应性”更强，插入的最坏情况是很难达成的，基本上每一次都不会走满，只有当“插入”的数据比前面的数据都小时，才需要走n次。但是冒泡是交换之后的两数进行比较————可以理解为，插入排序的比较的“基准”是不变的，一直是tmp，而冒泡排序的比较“基准”是在变化的，几乎每次都不一样

同时，冒泡排序想跳出循环的条件是极其苛刻的，基本上每次都会接近走满。

因此，冒泡几乎每次都是最坏，插入几乎都不会是最坏情况。

时间复杂度只计算最坏情况的大概时间，在具体的测试中差距可能非常巨大。

3. 堆排序

C语言数据结构基础笔记——树、二叉树简介-CSDN博客

对于堆排序，我们先使用“向上遍历的向下调整算法”建堆（复杂度是O(N)）.

若升序就建大堆，降序就建小堆，再利用HeapPop的思想，将根拿出来放到数组的末尾，

再让数组尾指针--，达到排序的目的复杂度是O(n logn)

void HeapSort(int* arr, int number) {//先对传进来的数组建堆for (int i = (number - 1 - 1) / 2; i>=0; i--) {AdjustDown(arr,i, number);}//再使用Pop的思想排序while (number > 0) {Swap(&arr[0], &arr[number - 1]);number--;AdjustDown(arr, 0, number);}
}

向下调整算法的实现：

void AdjustDown(int* arr,int parent, int number) {//假设法找孩子大小int child = 2 * parent + 1;while (child < number) {//建大堆if (child + 1 < number && arr[child + 1] > arr[child]) {child++;}if (arr[parent] < arr[child]) {Swap(&arr[parent], &arr[child]);parent=child;child = child * 2 + 1;}else {break;}}
}

再来监视一下时间复杂度明显更优秀的堆排序的实际运算时间：

（上一次比较插入和冒泡是在debug环境下跑的，这次是在realse环境下跑的，所以快了很多）

堆排序作为O(nlogn)，时间明显快于插入排序，唯独就是实现的代码较麻烦

4.希尔排序

希尔排序的本质是插入排序的优化。

我们先进行预排序。预排序目标：让数组更一步接近有序

我们在上文中提到，当一个数组越来越接近有序时，插入排序的速度就会更快。

所以我们通过分组的形式，先略微的让数组更加有序。

分组，也就是分gap。我们用以下数组进行说明：

也就是每个隔gap的数据归为一组，每一组先执行插入排序。

不难理解，gap为多大，就有多少个组

因为在遇到第一组的第一个gap位置的元素之前（也就是0+gap）,每一个数据都可以作为一组新的数据的头

先实现一组的预排序，再将每组的实现逻辑套入前gap个元素中，让每一组都实现预排序。

预排序的每一单趟排序中

n-gap让我们不再计数每一组中有多少元素，只要当剩下的空间被我当前组再加一个gap就会越界时，就会跳出循环。

 for (int j = 0; j < gap; j++) {for (int i = j; i + gap < n; i += gap) {int end = i;
int tmp = a[end + gap];while (end >= 0) {if (tmp < a[end]) {a[end + gap] = a[end];end -= gap;}else {break;}
}
a[end + gap] = tmp;}}

接下来，就是我们叹为观止计算机前辈们的智慧了。

gap越大，调整越快，但是不太接近有序；gap越小，调整越慢，但是更接近有序。

当gap为1时，就是插入排序、

所以，gap是和n有关系的一个值，我们来学习一下前辈们是如何控制gap的：

先让gap很大，进行一次全组全成员的预排序。

然后让gap变小一倍，再进行一次全组全成员的预排序

....................

数组越来越接近有序

....................

最后一次gap一定会变成1，完成一次几乎接近有序的插入排序。所以，希尔其实是优化过的插入排序

void ShellSort(int* a, int n) {for (int gap = 3; gap > 0; gap /= 2) {for (int j = 0; j < gap; j++) {for (int i = j; i + gap < n; i += gap) {int end = i;int tmp = a[end + gap];while (end >= 0) {if (tmp < a[end]) {a[end + gap] = a[end];end -= gap;}else {break;}}a[end + gap] = tmp;}}
}}

更进一步：

两层循环可以优化成一层循环，但是时间复杂度不变

（文案有错，应该修改为“上面是红色完了，再排黄色，再排蓝色”）

而现在的调整方式是，先调整红色的·第一二个，再调整绿色的第一二个，再调整紫色的第一二个，再调红色的第二三个.........

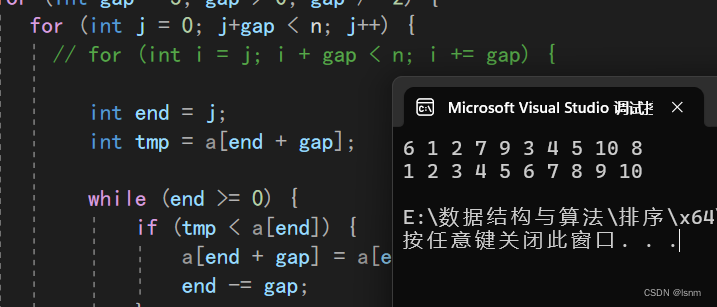
void ShellSort(int* a, int n) {for (int gap = 3; gap > 0; gap /= 2) {for (int j = 0; j+gap < n; j++) {// for (int i = j; i + gap < n; i += gap) {int end = j;int tmp = a[end + gap];while (end >= 0) {if (tmp < a[end]) {a[end + gap] = a[end];end -= gap;}else {break;}}a[end + gap] = tmp;
//	}}
}}

希尔排序的时间复杂度是一个极其复杂的问题：

有的人认为gap/2不是最优变化，(gap/3)+1才是最优变化，但是都没有得到严格的证明

——————出自严蔚敏老师的《数据结构（c语言版）》

以gap每次除以3为例：

gap=n/9时，可以推出一共有n/9组数据，每一组都有n/(n/9)=9个数据

只有第一组数据可以按照最坏情况来算，其他都会受到前面几次排序的增益

刚开始，逆序的话，最坏挪动n次，然后gap越来越小，需要调整的次数越多，但是前面的调整的增益也越来越大，最终增益大于gap变小带来的负面影响，整体次数开始减小

最终到最后一组的时候（也就是一次插入排序），已经非常接近有序，几乎就是遍历一遍数组，几乎不需要挪动。

通过统计学等相关知识，最后算出来应该是n^(1.3)，略大于nlogn

5.直接选择排序

我们先定义begin为0，end为最后一个数据的下标

遍历一遍数组，最大的放右边，最小的放左边，让begin增加,end减少，再重复以上操作.....

直到left与right重合

为什么换到 1 2 3 7 5 6 4 8 9 10时就换不动了呢？

当剩余数据比较少的时候，很有可能出现要交换的两组数据会重叠（minii和begin重叠、maxi和end重叠）

稍加if语句判断条件即可：

void SelectSort(int* a, int n) {int begin = 0, end = n - 1;int maxi = begin, mini = 0;for (; begin < end; begin++, end--) {for (int i = begin; i <= end; i++) {if (a[i] > a[maxi])maxi = i;if (a[i] < a[mini])mini = i;}Swap(&a[maxi], &a[end]);if(maxi!=begin)Swap(&a[mini], &a[begin]);}	 
}

6.快速排序☆☆

6.1快速排序基础

快速排序是 Hoare 于 1962 年提出的一种二叉树结构的交换排序方法，其基本思想为： 任取待排序元素序列中 的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右 子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止 。

其代码本质是一种递归排序

我们通常先选取最左段或者最右端作为key，也叫做关键字

此处我们以key在最左端,对数组{6,1,2,7,9,3,4,5,10,8}排升序为例讲解。

先看单趟：

为了让比key（对应的数，以下都称为key）大的数都在右端，比key小的数都存在左边，right下标的目标是找到比key小的数之后停下，left下标的目标是找到比key大的数之后停下。

先从right开始（从key所在端点的相反端点开始），向左找到5，然后left从key位置开始向右找“大”，找到7，交换5和7的位置，让小的数到接近key端点的方向，大的数到远离key端点的方向。交换完成之后，right再继续走，找到4，left找到9，再交换。最后，两者在下标为3的位置相遇，将相遇位置的值（3）和key进行交换。相遇位置的值一定小于key，这在后文会有具体解释，现在可以先记住结论。

至此，最神奇的发生了：key元素已经到了他该去的位置，因为左边全是比他小的，也只有比他小的。在升序的情况下，当比自己小的数据都放入数组后，就该放入自己了。

再以“分而治之”的二叉思想，将begin和keyi-1作为新的left和right传入我们上述的逻辑

在子数组{3,1,2,5,4}中排好3的位置。最后，当所有左子树都排好后再排右子树。

既然是二叉递归，那我们就需要把问题分割成：最小子问题（返回条件）和继续递归的部分。继续递归的部分已经在上文中陈述清楚，当要剩下的数组只有一个元素或者没有元素时（叶子结点），就不用再排序了（一个数据或没有数据一定是有序的），直接返回即可

代码实现：

因为我们会让left++和right--,所以在每次递归调用一开始时一定要记录左右端点，便于下次递归。

其次，我们应当一直对同一个数组进行操作，参数只传下标即可。

代码的实现应当先写出基本样式，可以有没考虑周全的部分，先实现出来大概再改善。

void QuickSort(int* a, int left,int right) {int begin = left, end = right;int key = left;while (left < right) {while (left<right && a[right]>a[key]) {//因为right一直--可能会越界，一直找不到时key就//是最小的数据，所以我们希望right此时能停留在最左断，与left、key处于同一位置right--;}while (left < right && a[left] < a[key]) {left++;}Swap(&a[left], &a[right]);}Swap(&a[key], &a[left]);//递归等会儿写
}

问题1：因为left一开始和key等值，所以此循环不会被调用

问题2：如果右边遇到一个和key相等的，左边也遇到一个和key相等的，就会进入死循环，不停的交换他们两个，所以两个小循环中应该需要取等。

改进之后：

void QuickSort(int* a, int left,int right) {if (left >= right)return;//排除无元素数组int begin = left, end = right;int key = left;while (left < right) {while (left<right && a[right]>=a[key]) {right--;}while (left < right && a[left] <= a[key]) {left++;}Swap(&a[left], &a[right]);}Swap(&a[key], &a[left]);key = left;//递归QuickSort(a, begin, key - 1);QuickSort(a, key+1, end);
}

现在解释，为什么left和right相遇位置的值一定小于key所对应的值：

根本原因在于：right先走。

正是因为right先走，所以当right停下时，其对应的数字一定小于key（或是直接走到key而与key相等），之后若被left在该点撞上，left和right进行无效对换，left和right共同指向的位置再与key交换，数值一定小于key，

若没有被left撞上，而是在之后的循环中right撞上了left，此情况一定发生在left和right已经发生过交换之后，那么较小值已经被换到了left所在位置，因此，若在left相遇，一定也是最小。

同理，也可以key在右边，left先走，任然是left找大，right找小。

最后相遇时对应的数据一定是大于key对应的数据。

6.2关于快速排序的时间复杂度

我们粗略的认为每一层就是把一整个数组分成两个，所以最坏情况下，分到最后的“最小子问题”时应该一共有logN层。对于每一层，都是左找到中间，右也找到中间，所以合起来是n次。另外，尽管每一层都会多出一些不用遍历的红色数字，但是几乎就在N的量级，因此一般情况下的复杂度是n*logn

快速排序最坏的时间复杂度是：有序

每次最小的都在最左端，key只会一个数据一个数据的变化，而每一次都需要把所有数据全部遍历完，复杂度是n(n+n-1+n-2+.......1),也就是n^2.

所以，这样的排序不适宜有序或者接近有序的数据，可能会直接超时并且栈溢出

但是一般情况下，key都会走到接近中间的位置。发生“有序”的困难程度堪比冒泡排序可以满足条件跳出循环的复杂程度，大部分情况下还是很好用的。

6.3随机数法和三数取中法

但是为了解决这个明显的弊端，有人想出了随机生成key位置的方法。

随机选出一个数据来和头位置数据交换，让这个随机的数字变为头数据，减弱数组本来很有序的可能性。随机取key和三数取中（后文有解释）两种方法，都能有效对抗原数组较有序的情况，能让较坏情况变为较好情况

比如本来是一个升序的有序数列 1,2,3,4,5,6,7,8,9.....，每一轮我都让中间的数作为key，所以每次都会几乎均分，每次都二分。

会不会出现，本来的有序性没有那么强，我将随机值与最左端（或最右端）一交换之后，

反而更有序了？

毕竟把一切都交给随机数并不是一个特别靠谱的办法。

于是，又有人给出了三数取中的办法：

在left、right、mid（mid=（right+left）/2）三个数中选出不大也不小的那个数，与一个端点进行交换，作为key————保证作为key的值不是最小或者最大

（每一次递归调用函数都会重新取一次key）

快速排序的优化（小区间优化）：

由二叉树的性质知道，二叉树消耗最大的是层底，也就是数组被分到最短的时候

二叉树的最后三层（以满二叉树为例），几乎占到（0.5+0.25+0.125）80%,而最后几层的数组又非常短，非常短的数组在排序时用各种方法消耗都不打，可以考虑在数组很短（比如小于十个时），考虑使用插入排序来排数组短于10~15个的小数组

二叉树的最下层是占比最大的

6.4其他的单趟实现方法

6.4.1挖坑法

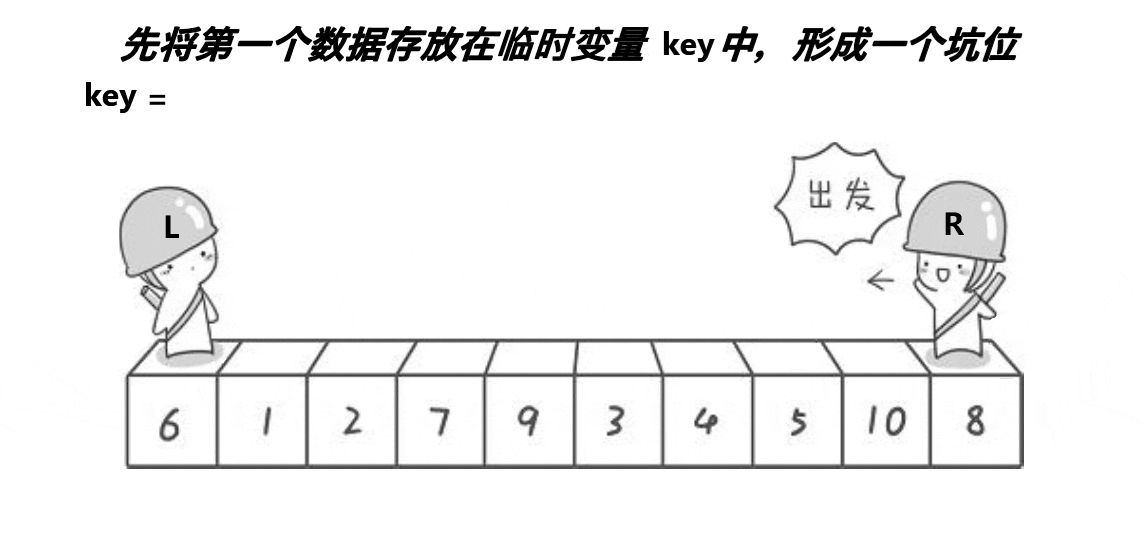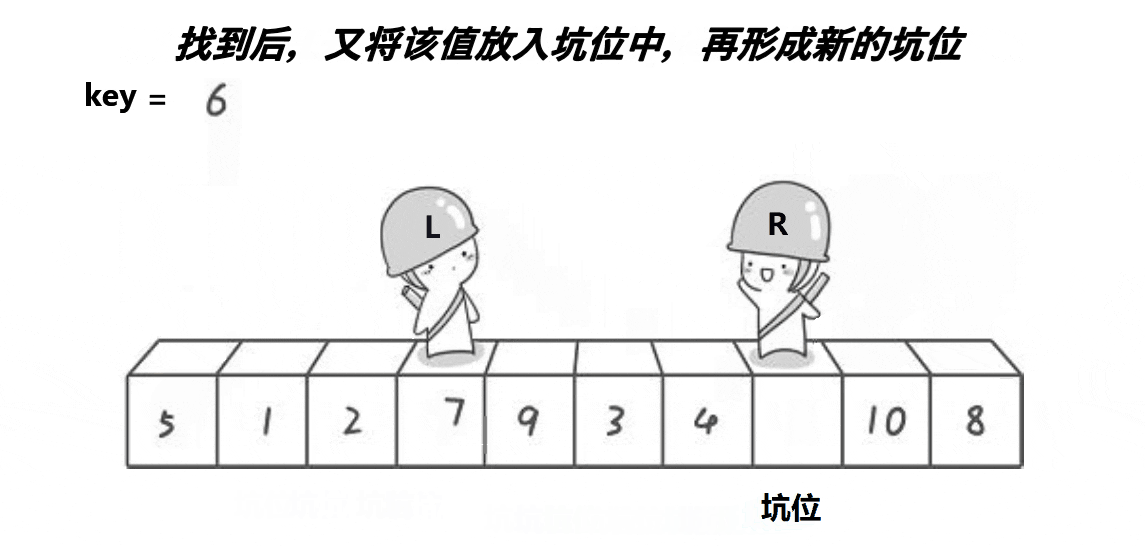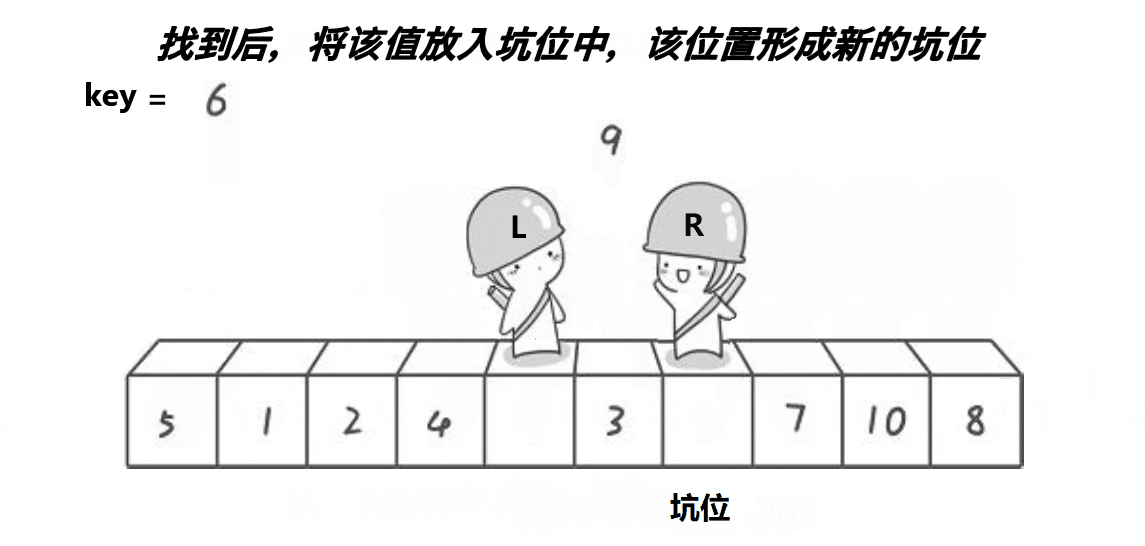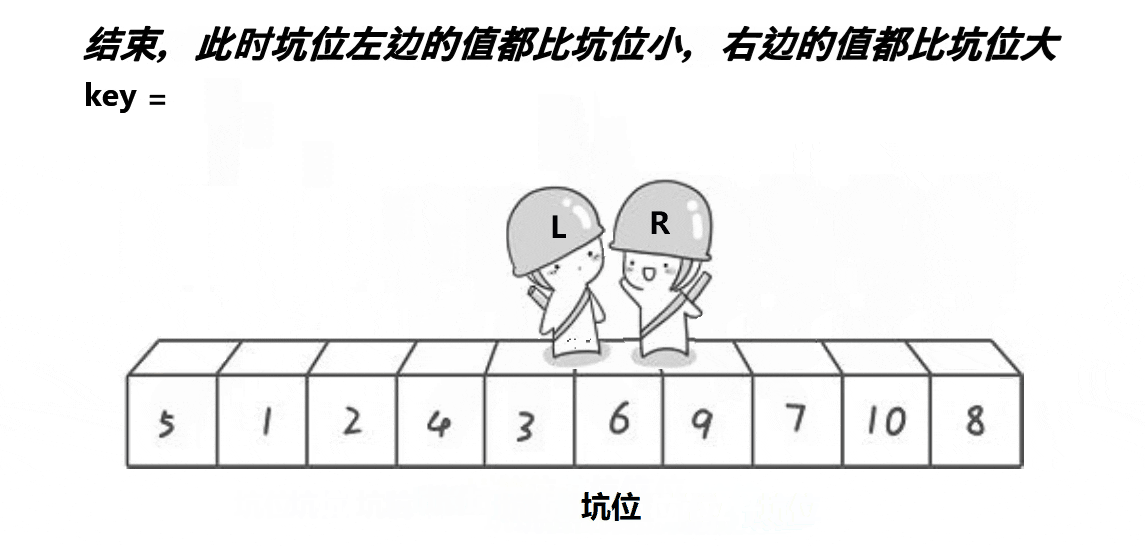先将Key位置的值挖出，当作坑，依然是右边先走，遇到小的数据就塞进坑去，并停在新的坑处

左边找大。

6.4.2前后指针版快速排序☆

初始状态，让prev指向key的位置，cur指向后一个的位置（下标为1）。

我们的目标是让cur和prev之间都是比key大的数据，prev及其左边都是小于key的数据

只要cur和prev形成路程差（如现在的初始状态），就比较cur的值是否大于等于key的值，

若确实大于key的值，就让cur++；若小于key的值，就让prev也++，交换prev和cur的值，让小值去的左端，并且cur++,继续判断下一个数据。最终交换成为：prev左边(包括prev自己)全是比key小的，右边全是比key大的

除非数组为空或者只有一个数据，Prev所在的位置对应的一定是被cur丢过来的较小数，所以不用担心在swap过程中把小的数又丢到右端的情况。因为prev和cur之间不会有较小数。

此种方法的优点就是，代码实现相对简单：

void QuickSort2(int left, int right, int* arr) {if (left >= right)return;int keyi = left;int prev = left;int cur = left + 1;while (cur <= right) {if (arr[cur] < arr[keyi]) {prev++;Swap(&arr[cur], &arr[prev]);//这一步，不会出现将两个较小数对调的情况}cur++;}Swap(&arr[keyi], &arr[prev]);keyi = prev;QuickSort2(left, keyi - 1, arr);QuickSort2(keyi+1, right, arr);
}

6.4.3非递归实现快排☆

有能力将递归方法改成非递归方法是程序员应该有的素养。

借用数据结构“栈”来将递归改成迭代

C语言基础数据结构——栈和队列-CSDN博客

将区间作为参数，以十个数据的数组为例：

先压入0~9,再取出0~9进行单趟，压入keyi+1 ,right和left,keyi-1

由于栈的特性，我们遵循递归方法的顺序，先压右边的，再压左边的，这样就能先调用左边的。拿出左边的区间，进行一次单趟，再压入新的keyi+1 ,right和left,keyi-1,直到这两个区间的距离<=1,就不再压入，而是取出栈中的元素重复以上操作。

（其实距离<=1就是递归方法中的两个最小子问题）

代码实现：

void QuickSortNonR(int* arr, int left, int right) {ST st;STInit(&st);STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)) {left = STTop(&st);STPop(&st);right = STTop(&st);STPop(&st);int prev = left, keyi = left;int cur = left + 1;while (cur <= right) {if (arr[cur] < arr[keyi]) {prev++;Swap(&arr[cur], &arr[prev]);}cur++;}Swap(&arr[keyi], &arr[prev]);keyi=prev;//(left,keyi-1) keyi (keyi+1,right)if (keyi + 1 < right) {//相当于是满足二叉树最小子问题的就不再入栈STPush(&st, right);STPush(&st, keyi+1);}if (left < keyi - 1) {STPush(&st, keyi-1);STPush(&st, left);}}STDestroy(&st);}

（也可以使用队列来实现，类似于层序。）

7.归并排序

7.1递归实现

在之前的练习题中我们有遇到过类似的问题，如两有序数组合并之后依然有序等问题，解决方法就是取小的数据然后在新数组尾差

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有 序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

但是不便于在原数组上进行，所以我们malloc出一个tmp数组。

将原数组均分成两个子数组，若两个子数组有序，就能通过取小的方式进行归并（顺序表、链表等同理）。但是子数组高概率是无序的，我们就需要对子数组继续分，直到分到每个子数组只有一个数据，满足“有序”条件

每一次归并完了就拷贝回去

比如数组{10,6,7,1,3,9,4,2}

先分成（10,6）（7,1）（3.9）（4,2），排好为(6,10),(1,7),(3,9),(2,4)，再将(6,10)和(1,7)进行归并......依次类推，直到最后一次由两个数组归并成原来大小的数组

代码实现：

因为不希望每次都开临时数组tmp，所以再写一个递归的子函数(_MergeSort)用于被主要的mergesort调用

一上来就先开个tmp:

因为此处开始递归的本质至少是针对两个数据（各自作为一个子数组而存在）

所以我们应当先深层递归，从(righ-left)==0的时候开始返回再开始第一次实质性的归并

又因为一开始我们归并的都是很小一部分数组，所以只能回传我们归并的部分，不然可能传入随机值，而由于传址调用的影响是永久的，传随机值进数组会有永久性伤害

所以我们还需要增加一个参数tmp

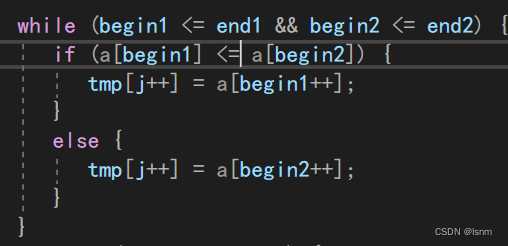
void _MergeSort(int left, int right, int* a,int* tmp) {if ((right - left) < 1)return;int mid = (left + right) / 2;//[left~mid] [mid+1~right]_MergeSort(left, mid, a,tmp);_MergeSort(mid+1, right, a,tmp);//归并int begin1 = left, end1 = mid, begin2 = mid + 1, end2 = right;int i = begin1;//作为临时数组的下标while (begin1 <= end1 && begin2 <= end2) {if (a[begin1] < a[begin2]) {tmp[i++] = a[begin1++];}else {tmp[i++] = a[begin2++];}       }while (begin1 <= end1) {tmp[i++] = a[begin1++];}while (begin2 <= end2) {tmp[i++] = a[begin2++];}memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));PrintArray(a, right-left+1);printf("\n");
}void MergeSort(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL) {perror("malloc failed!");exit(1);}_MergeSort(0 ,n-1 ,a,tmp);free(tmp);tmp = NULL;
}

传回时注意只传排好的，否则有可能通过a这个指针永久性伤害原数组

新tmp的下标i应该和begin1对应

7.2非递归实现

快排本质是前序，在每次递归之前都先解决一个数据的就位，因此能用栈解决非递归转递归的问题

但是归并是后序，用一个栈不方便解决问题。

因此，我们采取循环（迭代）的思想来

递归中，我们是将一个数组几乎分到只剩两个数据为一组。

循环的思想其实就是将递归中分而治之的思想跳过“分”，直接“制”

gap指的是每一组的元素个数，每次将相邻的两组进行归并

相当于是直接跳到最小子问题处，开始回归部分。

每一次是将两组进行归并

所以，每次排好序的都是2*gap个数据

最后，每一轮遍历完再将tmp拷回数组a.

以上方法仅支持个数是2的次方的。若数组元素为10，第一轮可以收，第二轮一共有5组，无法再两两配对，需要对begin1 end1 begin2 end2进行单独的条件判断：

不止第二轮，每一轮都可能遇到奇数的情况，目前的代码（如上图）只能解决二的次方倍个数的

（下标越界了）

首先由条件得，begin1不会越界，若end1或begin2就越界了（换句话说，就是该归并小组的右足完全不存在），就不用归并该小组了，也不需要使用memcpy返回

若只有end2越界（该归并小组的右组存在，但是不是满员并且至少有一个），则该小组依然需要归并，只是该小组的右组变小，但是调整end2即可。

最终实现：

void MergeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);//int gap = 1;//gap表示每一组的元素个数for (int gap = 1; gap <= n - 1; gap *= 2) {for (int i = 0; i<=n-1; i += gap * 2) {int begin1 = i, end1 = begin1 + gap - 1;int begin2 = end1 + 1, end2 = begin2 + gap - 1;//减1的原因就是植树问题int j = begin1;//判断几个下标的条件if (end1 > n - 1 || begin2 > n - 1) {end1 = n - 1;begin2 = end2 + 1;}else if (end2 > n - 1) {end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2) {if (a[begin1] < a[begin2]) {tmp[j++] = a[begin1++];}else {tmp[j++] = a[begin2++];}}while (begin1 <= end1) {tmp[j++] = a[begin1++];}while (begin2 <= end2) {tmp[j++] = a[begin2++];}}memcpy(a, tmp, n*sizeof(int));}}

（判断下标条件中，若end1或begin2越界，相当于右侧的归并小组已经不存在，不需要和左侧的一起归并，直接把数组末尾两组中左侧的那组留到下一组进行归并即可。若发生上述情况，为了不让右侧的数组再进入归并，我们直接让begin2大于end2，从而不再进入下面的条件语句）。

8.计数排序

以上所有排序内容，都是通过比较来排序。

常见的非比较排序有：计数排序、桶排序、基数排序。

此处只介绍最常见的一种：计数排序

（非比较排序相对于比较排序，运用场景更小更窄，局限性较强）

具体思想为：

1. 统计相同元素出现次数

2. 根据统计的结果将序列回收到原来的序列中

适用于统计数据大小范围集中且有数据重复的数据，比如一个班的身高、体重等

其排序比大小的过程在创建“记录数组”时就已经自然产生了

对于集中的数据，这是一种“秒杀”的排序方法：

对于数据范围和个数接近的数组，其复杂度就是遍历一遍数组，也就是O(n)，空间复杂度也是O(n)

但是局限性很明显，排不了浮点数，排不了字符串，排不了结构体。

整形是很便于映射到数组中，但是其他类型就会比较麻烦了，因此说他是一个小众的排序方法。

代码实现如下：

calloc的目的是让里面的数据初始化为0，方便++

9.小结

在比较排序中：

稳定性：一组数据中，在排序后，两个相同的数值的相对顺序变不变，表示有无稳定性

不变就是稳定的，变就是不稳定的。

我们从时间复杂度、空间复杂度、以及稳定性的角度来回顾一下各种排序：

插入排序的基础是直接插入排序，直接插入排序就是打扑克牌中理牌的过程，越接近有序则也不需要理，最坏情况是每一张都要理到头，一共是等差数列求和，所以时间复杂度是O(N^2),不需要额外的空间，空间复杂度是O(1)。由于是按照顺序插入和遍历，所以是有序的。希尔排序是直接插入排序的进阶和优化，时间复杂度较特殊，为O(N^1.3);空间复杂度也是原地空间，但是由于相同大小的数据由于在分gap时可能被分到不同的组，所以不具有稳定性。

直接选择排序就是遍历整个数组找大找小放两头，时间复杂度也是等差数列求和:O(N^2)

不需要额外空间，对于稳定性：

直接选择排序：

在只选一个最小的到左边情况下，1能做到稳定，3能做到稳定吗？

而堆排序是经典的nlogn,需要建堆（可以原地建堆），一定是不稳定的。

对于最差的冒泡排序，时间复杂度为O(N^2),空间为原地算法。一定是可以做到稳定的，我们只需要让相等的数据在相邻相遇时不交换即可。快速排序中，每次都是确定并移动key的位置，时间复杂度O（NlogN）,空间复杂度由于递归的存在，每一层递归都要建立相应的函数栈帧，一共递归N层，所以是logN,对于稳定性：

、

最左端的key是5，请问他就位之后还是第一个5吗？