在众多的排序算法中，堆排序以其独特的性质和高效的性能脱颖而出。堆排序算法利用堆这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组来模拟堆的结构以进行排序。堆排序可以分为两个主要的过程：建堆和堆调整。

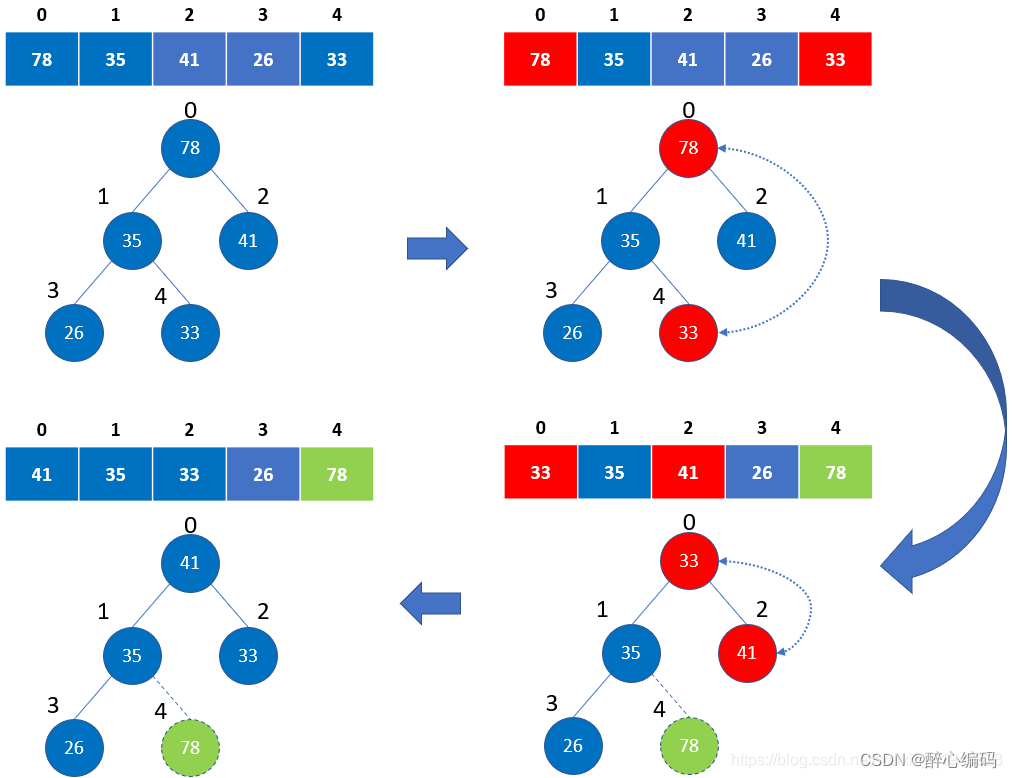
一、堆排序的基本概念

堆排序（Heap Sort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子节点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种树形选择排序，是对直接选择排序的有效改进。堆的定义如下：具有n个元素的序列（h1,h2,…,hn),当且仅当满足（hi>=h2i,hi>=2i+1）或（hi<=h2i,hi<=2i+1） (i=1,2,…,n/2)时称之为堆。在这里只讨论满足hi>=h2i且hi>=2i+1的堆称为大根堆，亦称最大堆或最大完全二叉树。堆排序是一种树形选择排序方法，是对直接选择排序的有效改进。

堆的定义如下：具有n个元素的序列（h1,h2,…,hn),当且仅当满足（hi>=h2i,hi>=2i+1）或（hi<=h2i,hi<=2i+1） (i=1,2,…,n/2)时称之为堆。在这里只讨论满足hi>=h2i且hi>=2i+1的堆称为大根堆，亦称最大堆或最大完全二叉树。堆中最大元素值总是在堆的根节点上。堆中任一非终端节点的数据值均不小于其左子节点和右子节点的值。堆排序就是利用堆进行排序的方法。它的基本思想是：将待排序的序列构造成一个大顶堆。此时，整个序列的最大值就是堆顶的根节点。将它移走（其实就是将其与堆数组的末尾元素交换，此时末尾元素就为最大值），然后将剩余的n-1个序列重新构造成一个堆，这样会得到n个元素中的次大值。如此反复执行，便能得到一个有序序列了。

二、堆排序的主要过程

堆排序包括两个主要的过程：建堆和堆调整。

建堆

建堆，就是将一个无序的序列调整成为一个大顶堆（或小顶堆）。在堆中，父节点的值总是大于或等于（或小于或等于）它的子节点的值。在堆排序算法中，我们通常采用大顶堆。

建堆的过程，是从最后一个非叶子节点开始，将其调整成为堆。然后向前依次调整每一个非叶子节点，直到整个序列都成为堆。具体步骤如下：

（1）将n个待排序的元素构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。

（2）将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个序列重新构造成一个堆，这样会得到n个元素中的次大值。如此反复执行，便能得到一个有序序列了。

建堆的时间复杂度是O(n)。

堆调整

堆调整的过程，其实就是删除堆顶元素，然后将剩余元素重新调整成为堆的过程。具体步骤如下：

（1）删除堆顶元素。

（2）将堆尾元素放到堆顶。

（3）从堆顶开始向下调整堆。具体调整方法是从堆顶开始，将其与左子节点和右子节点比较，如果比子节点小，则与子节点中较大的一个交换。然后继续向下调整，直到叶子节点或者比子节点大为止。

堆调整的时间复杂度是O(logn)。

三、堆排序算法的特点

堆排序算法的主要特点如下：

堆排序是不稳定的排序方法。
堆排序的时间复杂度为O(nlogn)。
堆排序的空间复杂度为O(1)。

四、堆排序的C代码实现

以下是堆排序的C代码实现：

#include <stdio.h>  void swap(int* a, int* b) {  int t = *a;  *a = *b;  *b = t;  
}  void heapify(int arr[], int n, int i) {  int largest = i;  // Initialize largest as root  int left = 2 * i + 1;  // left = 2*i + 1  int right = 2 * i + 2;  // right = 2*i + 2  //如果左子节点比根节点大，则更新最大值
if (left < n && arr[left] > arr[largest])
largest = left;// 如果右子节点比目前已知的最大值还大，则更新最大值  
if (right < n && arr[right] > arr[largest])  largest = right;  // 如果最大值不是根节点  
if (largest != i) {  swap(&arr[i], &arr[largest]);  // 递归地调整受影响的子堆  heapify(arr, n, largest);  
}
}void heapSort(int arr[], int n) {
// 建堆
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);// 一个个从堆顶取出元素  
for (int i = n - 1; i >= 0; i--) {  // 将当前最大的元素arr[0]与arr[i]交换  swap(&arr[0], &arr[i]);  // 调整剩余元素，使其重新成为堆  heapify(arr, i, 0);  
}
}void printArray(int arr[], int n) {
for (int i = 0; i < n; ++i)
printf("%d ", arr[i]);
printf("\n");
}int main() {
int arr[] = {12, 11, 13, 5, 6, 7};
int n = sizeof(arr) / sizeof(arr[0]);heapSort(arr, n);  printf("Sorted array is \n");  
printArray(arr, n);
}

这段代码首先定义了一个swap函数用于交换两个元素的值，然后定义了heapify函数用于调整堆。在heapSort函数中，首先通过heapify函数将数组构造成一个大顶堆，然后依次将堆顶元素与末尾元素交换，并重新调整堆，直到整个数组有序。

堆排序的时间复杂度是O(nlogn)，其中建堆的时间复杂度是O(n)，堆调整的时间复杂度是O(logn)，总共需要进行n次堆调整。因此，堆排序是一种高效的排序算法，适用于处理大量数据。

需要注意的是，堆排序是一种不稳定的排序算法，即相同元素的相对顺序在排序过程中可能会发生改变。如果需要稳定的排序算法，可以考虑使用归并排序或冒泡排序等算法。