神秘题目。
题目的条件十分神奇,\(|A| \le \frac{1}{5} (s+p)\),不知所云。
一开始尝试用皮克定理转化,但是 failed。
阅读理解之后发现有一个(很典)的套路,就是构造出五组方案,使得 \(\sum_{cyc} |A| = s+p\),这样就一定有一组方案,面积小于等于 $ \frac{1}{5} (s+p)$。
如何构造?
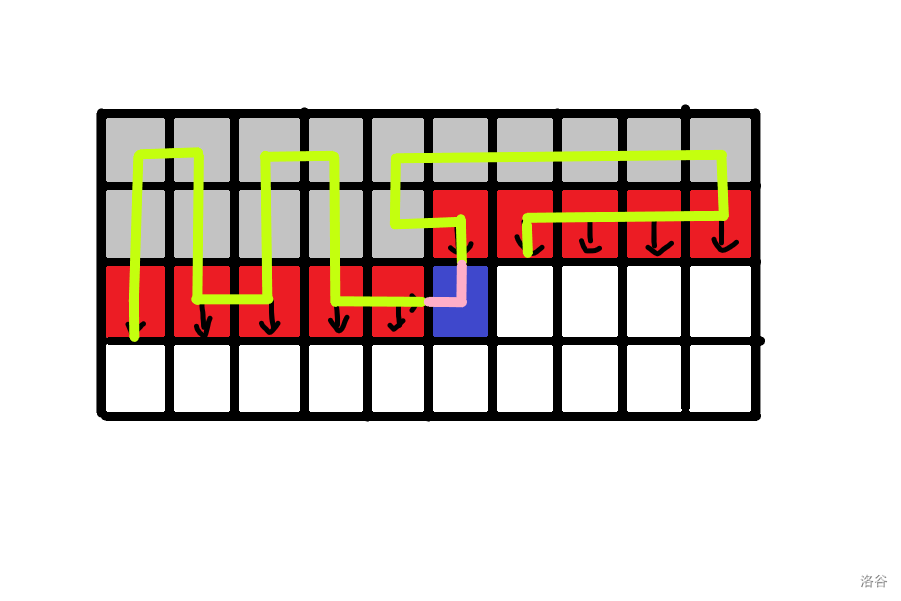
我们发现一个格子可以【控制】周围四个,带上自己五个格子。差不多这样:

发现如果按照 \((2i+j) \mod 5\) 的余数来分类的话,总共五种方案,刚好每一种余数可以【密铺】整个地图。显然,这样覆盖,五种方案个数和是 \(s\)。
同时,对于边界上的没有覆盖到的,我们直接花一个方格放上去。可以证明(懒),这样带来的额外代价之和就是 \(p\)。(感性理解就是只有边界上的格子会额外贡献,且有几条边【孤立】就会额外贡献几遍)
于是我们构造出来这五种方案,取个最小值就是一组可行的解。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define all(v) v.begin(), v.end()
using namespace std;//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
#define multi_cases 1namespace Traveller {const int N = 2e6+2;const int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};int n, m;int pos(int i, int j) { return (i-1) * m + j; }char g[N];bool mark[N];char ans[5][N];void main() {cin >> n >> m;for(int i = 1; i <= n; ++i) for(int j = 1; j <= m; ++j) cin >> g[pos(i, j)];for(int i = 1; i <= n; ++i)for(int j = 1; j <= m; ++j) for(int k = 0; k < 5; ++k) ans[k][pos(i, j)] = 0;int mn = inf, p = 0;for(int k = 0; k < 5; ++k) {int cnt = 0;for(int i = 1; i <= n; ++i)for(int j = 1; j <= m; ++j) mark[pos(i, j)] = 0;for(int i = 1; i <= n; ++i)for(int j = 1; j <= m; ++j)if(g[pos(i, j)] == '#' && (2*i + j) % 5 == k) {mark[pos(i, j)] = 1;++cnt, ans[k][pos(i, j)] = 'S';for(int d = 0; d < 4; ++d) {int nx = i + dir[d][0], ny = j + dir[d][1];if(nx < 1 || nx > n || ny < 1 || ny > m || g[pos(nx, ny)] == '.') continue;mark[pos(nx, ny)] = 1; }}for(int i = 1; i <= n; ++i)for(int j = 1; j <= m; ++j) if(g[pos(i, j)] == '#' && !mark[pos(i, j)]) {++cnt, ans[k][pos(i, j)] = 'S';mark[pos(i, j)] = 1;}if(cnt < mn) mn = cnt, p = k;}for(int i = 1; i <= n; ++i, puts(""))for(int j = 1; j <= m; ++j)if(ans[p][pos(i, j)] == 'S') cout << 'S';else cout << g[pos(i, j)];}
}signed main() {
#ifdef filenameFileOperations();
#endifsigned _ = 1;
#ifdef multi_casesscanf("%d", &_);
#endifwhile(_--) Traveller::main();return 0;
}