TOP100-回溯（二）-编程知识

4.39. 组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates =[2,3,6,7],target =7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5],target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates =[2],target = 1
输出: []

提示：

1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40

思路：

本题没有数量要求，可以无限重复，但是有总和的限制，所以间接的也是有个数的限制。因为本题没有组合数量要求，仅仅是总和的限制，所以递归没有层数的限制，只要选取的元素总和超过target，就返回！

代码：

// 剪枝优化
class Solution {public List<List<Integer>> combinationSum(int[] candidates, int target) {List<List<Integer>> res = new ArrayList<>();Arrays.sort(candidates); // 先进行排序backtracking(res, new ArrayList<>(), candidates, target, 0, 0);return res;}public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {// 找到了数字和为 target 的组合if (sum == target) {res.add(new ArrayList<>(path));return;}for (int i = idx; i < candidates.length; i++) {// 如果 sum + candidates[i] > target 就终止遍历if (sum + candidates[i] > target) break;path.add(candidates[i]);backtracking(res, path, candidates, target, sum + candidates[i], i);path.remove(path.size() - 1); // 回溯，移除路径 path 最后一个元素}}
}

Python:

class Solution:def backtracking(self, candidates, target, total, startIndex, path, result):if total == target:result.append(path[:])returnfor i in range(startIndex, len(candidates)):if total + candidates[i] > target:continuetotal += candidates[i]path.append(candidates[i])self.backtracking(candidates, target, total, i, path, result)total -= candidates[i]path.pop()def combinationSum(self, candidates, target):result = []candidates.sort()  # 需要排序self.backtracking(candidates, target, 0, 0, [], result)return result

5.22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

提示：

1 <= n <= 8

思路：

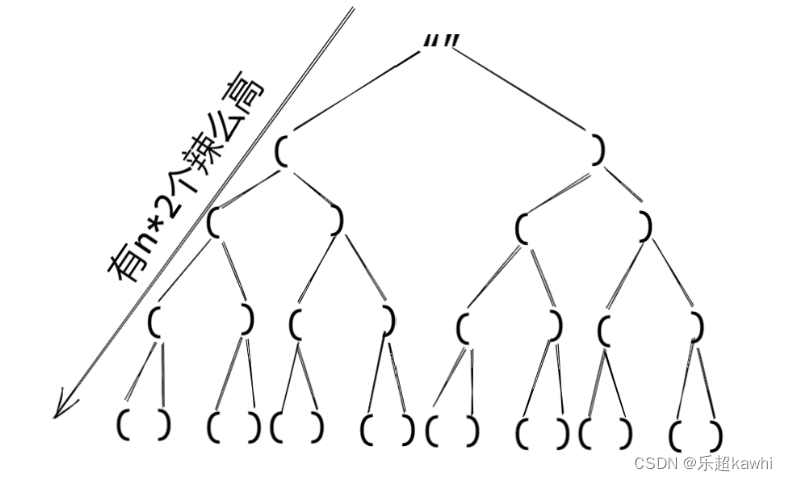
回溯法，想象是否成功，通通建立2*n高的树，设置左右标志；加入左括号，则左标志+1，加入右括号，则右标志+1；仅当到达叶子节点时，左右标志也为n，才算做正确的输出。

代码：

class Solution:def generateParenthesis(self, n: int) -> List[str]:if n<=0:return []res = []def dfs(paths,left,right):if left>n or right >left: return#左括号多了，和右括号大于左括号数时，直接拜拜if len(paths) == n*2:res.append(paths)returndfs(paths+'(',left+1,right)dfs(paths+')',left,right+1)dfs('',0,0)return res

6.79. 单词搜索

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true
示例 2：
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true
示例 3：
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false
提示：

m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成

思路：

思路也应该就是深度优先搜索，然后剪枝。关键点在于：当访问到的位置不是下一个预期值时，直接跳出，然后回溯，不继续下去。

代码：

class Solution {public int m;public int n;public boolean exist(char[][] board, String word) {m=board.length;n=board[0].length;char[] words=word.toCharArray();for(int i =0;i<m;i++){for(int j = 0;j<n;j++){if(dfs(board,words,i,j,0))return true;}}return false;}boolean dfs(char[][] board,char[] word,int i,int j,int k){if(i>=m || i<0 || j>=n || j<0 || board[i][j] != word[k])return false;if(k == word.length-1)return true;board[i][j]='\0';boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) || dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);board[i][j] = word[k];return res;}
}

7.131. 分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串。返回 s 所有可能的分割方案。

示例 1：
输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]
示例 2：
输入：s = "a"
输出：[["a"]]
提示：

1 <= s.length <= 16
s 仅由小写英文字母组成

思路：

1.先写一个函数用于判断是否为回文串
2.要划分出所有的子串，就是通过构建树来完成，而这个过程会用到深度优先搜索dfs(i)这个i是指第i个以后还没有遍历处理，而不是对第i个做操作,子串操作s.substring(start,end+1)
其他内容详见

代码：

class Solution {private String s;private final List<List<String>> res = new ArrayList<>();private final List<String> path = new ArrayList<>();//路径变量public List<List<String>> partition(String s) {this.s=s;//首先给字符串赋值//开始回溯（递归寻找）dfs(0,0);return res; }private boolean isHuiWen(int left, int right){while(left<right)if(s.charAt(left++)!=s.charAt(right--))return false;return true;}//i后面的还没处理，从Start开始private void dfs(int i, int  start){if(i==s.length()){res.add(new ArrayList<>(path));//说明这个已经完成了，复制return;}//不选i与i+1之间的逗号if(i < s.length() - 1)dfs(i+1,start);// 选 i 和 i+1 之间的逗号（把 s[i] 作为子串的最后一个字符）//要对于检查回文的部分做操作，也就是把s[i]作为字符串的最后一个字符,//需要判断从start到iif(isHuiWen(start,i)){path.add(s.substring(start,i+1));//切割子串，第i+1不算入//判断下一个字符作为头dfs(i+1,i+1);path.remove(path.size()-1);//恢复现场}}}

8.51. N 皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

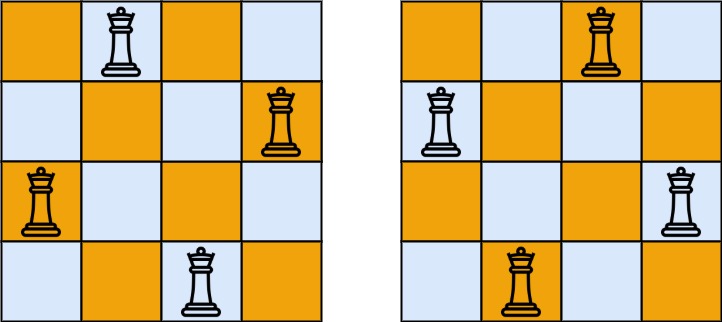
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

1 <= n <= 9

思路：

首先，抄来回溯的模板：

void backtracking(参数){if(终止条件){存结果;return;        }for(选择:本层集合中元素（树中节点孩子的数量就是集合的大小）){处理节点；backtracking（路径，选择列表）；//递归回溯，撤销处理结果;}}

递归函数参数：

依然是定义全局变量二维数组result来记录最终的结果。

参数n是棋盘的大小，然后用row来记录当前遍历到了棋盘的第几层

这部分代码是：

result=[[]*n]*n
def backtrak(n , row , chessboard):#chessboard为棋盘

我们是逐行去寻找的，因此可以想到当当前遍历行数row为第n行时，回溯到了终点。因此回溯终点为：

if row == n :result.push_back(chessboard)return

单层搜索的逻辑：

递归深度其实就是row控制棋盘的行，每一层里for循环的col控制棋盘的列，一行一列决定了皇后的位置。
每次都是从新的一行开始搜索，因此都是从0开始

代码如下：

for(int col = 0; col < n ; col++){if(isValid(row,col,chessboard,n))chessboard[row][col] = 'Q';backtrack(n,row+1,chessboard);chessboard[row][col] = '.';    
}

验证是否合法的逻辑是：

1.不能同行
2.不能同列
3.不能同斜线（45度和135度）

代码：

bool isVaild(int row,int col, vector<string>& chessboard , int n){for(int i= 0;i < row ; i++){//同一列if(chessboard[i][col]=='Q')return false;}//45度检查for(int i= row-1 ,int j =col-1;i >=0 && j >=0 ; i--,j--){if(chessboard[i][j]=='Q')return false;    }//135度检查for(int i= row-1 ,int j =col+1;i >=0 && j < n  ; i--,j++){if(chessboard[i][j]=='Q')return false;  }return true;}

总结来说：

棋盘的宽度就是for循环的长度，递归的深度就是棋盘的高度，这样就可以套进回溯法的模板里了。

代码：

class Solution:def solveNQueens(self, n: int) -> List[List[str]]:result = []  # 存储最终结果的二维字符串数组chessboard = ['.' * n for _ in range(n)]  # 初始化棋盘self.backtracking(n, 0, chessboard, result)  # 回溯求解return [[''.join(row) for row in solution] for solution in result]  # 返回结果集def backtracking(self, n: int, row: int, chessboard: List[str], result: List[List[str]]) -> None:if row == n:result.append(chessboard[:])  # 棋盘填满，将当前解加入结果集returnfor col in range(n):if self.isValid(row, col, chessboard):chessboard[row] = chessboard[row][:col] + 'Q' + chessboard[row][col+1:]  # 放置皇后self.backtracking(n, row + 1, chessboard, result)  # 递归到下一行chessboard[row] = chessboard[row][:col] + '.' + chessboard[row][col+1:]  # 回溯，撤销当前位置的皇后def isValid(self, row: int, col: int, chessboard: List[str]) -> bool:# 检查列for i in range(row):if chessboard[i][col] == 'Q':return False  # 当前列已经存在皇后，不合法# 检查 45 度角是否有皇后i, j = row - 1, col - 1while i >= 0 and j >= 0:if chessboard[i][j] == 'Q':return False  # 左上方向已经存在皇后，不合法i -= 1j -= 1# 检查 135 度角是否有皇后i, j = row - 1, col + 1while i >= 0 and j < len(chessboard):if chessboard[i][j] == 'Q':return False  # 右上方向已经存在皇后，不合法i -= 1j += 1return True  # 当前位置合法