二分查找
二分查找模板题:704. 二分查找
二分查找前提:
- 有序数组
- 数组中无重复元素
左闭右闭:
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1;while (left <= right) {int mid = left + ((right - left) / 2);if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] < target) {left = mid + 1;} else return mid;}return -1;}
};
左闭右开
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size();while (left < right) {int mid = left + ((right - left) / 2);if (nums[mid] > target) {right = mid;} else if (nums[mid] < target) {left = mid + 1;} else return mid;}return -1;}
};
时间复杂度: O ( l o g n ) O(logn) O(logn)
空间复杂度: O ( 1 ) O(1) O(1)
二分查找拓展题:
【1】35.搜索插入位置
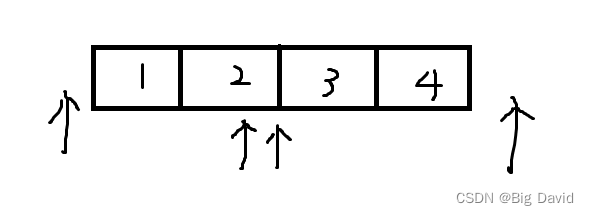
有两种情况考虑:
- 在数组中:二分查找
- 不在数组中:
- 所有数之前
- 在某两数之间
- 在所有数之后
而不在数组中即在二分查找的基础上改变退出循环后返回的值
二分查找退出循环时,左闭右闭left=right+1,左闭右开left=right
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = (left + right) / 2;if (nums[mid] > target) right = mid - 1;else if (nums[mid] < target) left = mid + 1;else return mid;}return right + 1;}
};
时间复杂度: O ( l o g n ) O(logn) O(logn)
空间复杂度: O ( 1 ) O(1) O(1)
【2】69. x 的平方根
class Solution {
public:int mySqrt(int x) {int left = 0; int right = x;while (left <= right) {int mid = (left + right) / 2;if ((long long)mid * mid > x) right = mid - 1;else if ((long long)mid * mid < x) left = mid + 1;else return mid;}return right;}
};
【3】367. 有效的完全平方数
class Solution {
public:bool isPerfectSquare(int num) {int left = 0; int right = num;while (left <= right) {int mid = (left + right) / 2;if ((long long)mid * mid > num) right = mid - 1;else if ((long long)mid * mid < num) left = mid + 1;else return true;}return false;}
};
【4】34. 在排序数组中查找元素的第一个和最后一个位置
两次二分,定义新变量first、last
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {if (nums.size() == 0) return vector<int>{-1, -1};int left = 0;int right = nums.size() - 1;int first = -1; int last = -1;while (left <= right) {int mid = (left + right) / 2;if (nums[mid] > target) right = mid - 1;else if (nums[mid] < target) left = mid + 1;else {first = mid;right = mid - 1;}}left = 0;right = nums.size() - 1;while (left <= right) {int mid = (left + right + 1) / 2;if (nums[mid] > target) right = mid - 1;else if (nums[mid] < target) left = mid + 1;else {last = mid;left = mid + 1;}}return vector<int>{first, last};}
};
【5】74. 搜索二维矩阵
二维转一维
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size();int n = matrix[0].size();int left = 0;int right = m * n - 1;while (left <= right) {int mid = (left + right) / 2;int x = matrix[mid / n][mid % n];if (x > target) right = mid - 1;else if (x < target) left = mid + 1;else return true;}return false;}
};
【6】33. 搜索旋转排序数组
通过二分找到旋转点,在区间内部二分找到目标值
class Solution {
public:int search(vector<int>& nums, int target) {if (nums.size() == 0) return -1;if (nums.size() == 1) {if (nums[0] == target) return 0;else return -1;}int left = 0, right = nums.size() - 1;while (left <= right) {int mid = (left + right) / 2;if (nums[mid] == target) return mid;if (nums[left] <= nums[mid]) {if (nums[left] <= target && nums[mid] >= target) right = mid - 1;else left = mid + 1;} else {if (nums[right] >= target && nums[mid] <= target) left = mid + 1;else right = mid - 1;}}return -1;}
};
【7】153. 寻找旋转排序数组中的最小值
class Solution {
public:int findMin(vector<int>& nums) {int left = 0;int right = nums.size() - 1;while (left <= right) {int mid = (left + right) / 2;if (nums[mid] < nums[right]) right = mid;else if (nums[mid] > nums[right]) left = mid + 1;else return nums[mid];}return nums[left];}
};