矩阵的归一化(Normalization)是将矩阵中的元素缩放到一个特定的范围或者标准,使得在进行比较、评估或计算时能够保持数值稳定性和可比性。这个过程在数据预处理、机器学习、图像处理等领域中非常重要。归一化有助于改善算法的收敛速度和精度,并且可以防止数值计算中的某些问题(如浮点溢出)。下面是几种常见的归一化技术:
1. 最小-最大归一化
这是最常见的归一化形式,也称作“线性归一化”,它将所有数值调整到0到1的范围内。对于矩阵中的每个元素,应用以下公式:

2. Z分数归一化(标准化)
这种方法基于原始数据的均值(μ)和标准差(σ),将数据转换为一个标准正态分布,均值为0,标准差为1。公式如下:
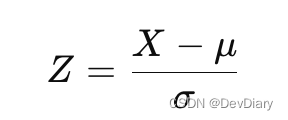
Z分数归一化对于假设数据遵循高斯分布(正态分布)的算法特别有用。
3. L1范数归一化
L1归一化,也称为最小绝对值和标准化,通过将特征向量的每个元素除以特征向量的所有元素绝对值之和来进行归一化。这样做可以使向量的L1范数(即向量元素绝对值的和)为1。
4. L2范数归一化
L2归一化,也称为最小二乘标准化,通过将特征向量的每个元素除以特征向量的欧几里得长度(即,根据平方和的平方根)来进行归一化。这会使得向量的L2范数(向量的欧几里得长度)为1。
每种归一化技术都有其特定的应用场景和优点。选择哪一种取决于具体的问题和数据的性质。例如,最小-最大归一化在保持相对大小关系方面很有用,但它对异常值非常敏感;而Z分数归一化在数据遵循正态分布时特别有效。L1和L2归一化在处理稀疏数据时特别有用,如文本分类和聚类问题。