#include <stdio.h>
#include <stdlib.h>typedef char BiElemType;
typedef struct BiTNode{BiElemType c;//c 就是书籍上的 datastruct BiTNode *lchild;struct BiTNode *rchild;
}BiTNode,*BiTree;//tag 结构体是辅助队列使用的
typedef struct tag{BiTree p;//树的某一个结点的地址值struct tag *pnext;
}tag_t,*ptag_t;
//递归实现
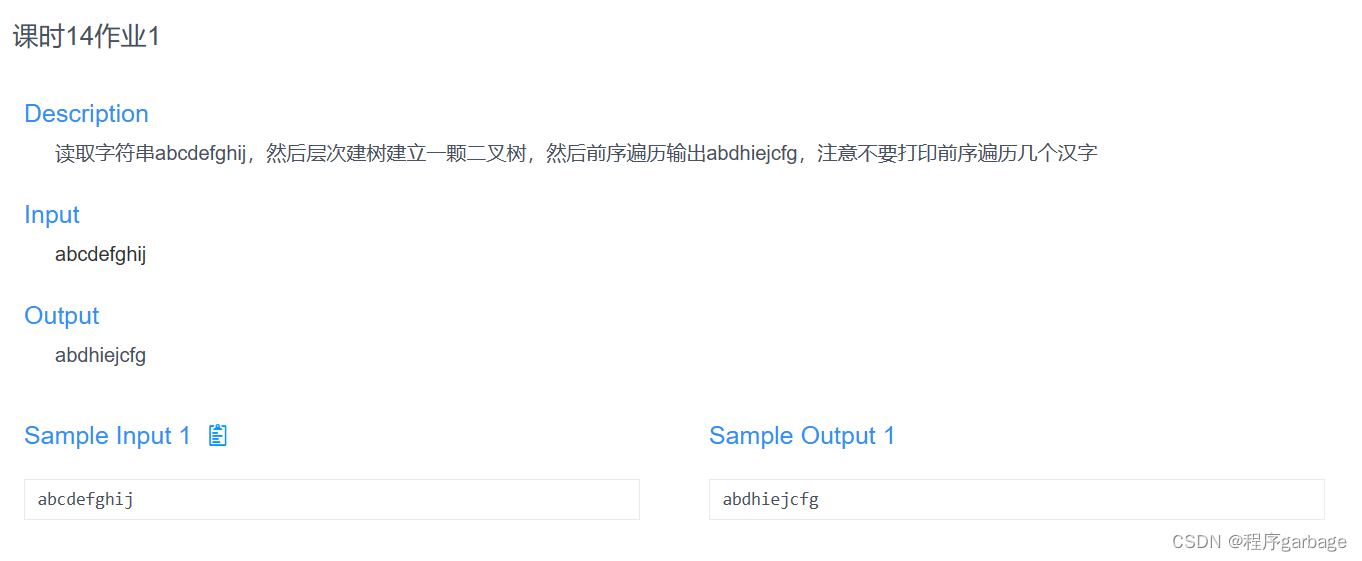
//abdhiejcfg 前序遍历 ,前序遍历就是深度优先遍历
void PreOrder(BiTree p)
{if(p!=NULL){putchar(p->c);//等价于 visit 函数PreOrder(p->lchild);PreOrder(p->rchild);}
}
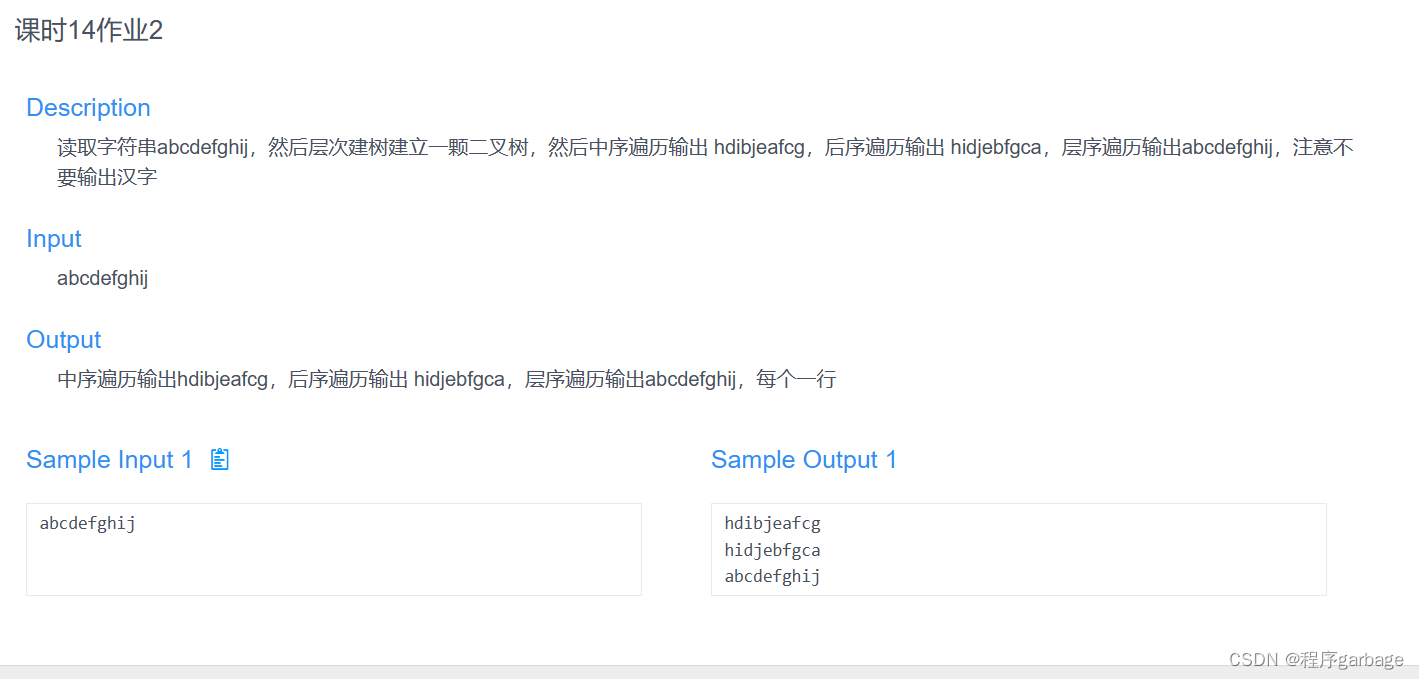
//中序遍历 hdibjeafcg
void InOrder(BiTree p)
{if(p!=NULL){InOrder(p->lchild);putchar(p->c);InOrder(p->rchild);}
}
//hidjebfgca 后序遍历
void PostOrder(BiTree p)
{if(p!=NULL){PostOrder(p->lchild);PostOrder(p->rchild);putchar(p->c);}
}
//《王道 C 督学营》课程
//二叉树的建树(层次建树)
int main()
{BiTree pnew;//用来指向新申请的树结点char c;BiTree tree=NULL;//树根
//phead 就是队列头 ,ptail 就是队列尾ptag_t phead=NULL,ptail=NULL,listpnew=NULL,pcur=NULL;
//输入内容为 abcdefghijwhile(scanf("%c",&c)){if(c=='\n'){break;}pnew=(BiTree)calloc(1,sizeof(BiTNode));//calloc 申请空间并对空间进行初始化 ,赋值为 0pnew->c=c;//数据放进去listpnew=(ptag_t)calloc(1,sizeof(tag_t));//给队列结点申请空间listpnew->p=pnew;if(NULL==tree){tree=pnew;//树的根phead=listpnew;//队列头ptail=listpnew;//队列尾pcur=listpnew;continue;}else{ptail->pnext=listpnew;//新结点放入链表 ,通过尾插法ptail=listpnew;//ptail 指向队列尾部}//pcur 始终指向要插入的结点的位置if(NULL==pcur->p->lchild)//如何把新结点放入树{pcur->p->lchild=pnew;//把新结点放到要插入结点的左边}else if(NULL==pcur->p->rchild){pcur->p->rchild=pnew;//把新结点放到要插入结点的右边pcur=pcur->pnext;//左右都放了结点后 ,pcur 指向队列的下一个}}//printf("--------Preface traversal----------\n");//也叫先序遍历 ,先打印当前结点 ,打印左孩子 ,打印右孩子PreOrder(tree);
// printf("\n--------Middle order traversal------------\n");//先打印左孩子 ,打印父亲 ,打印右孩子
// InOrder(tree);
// printf("\n--------Sequential traversal-----------\n");//先打印左孩子 ,打印右孩子 ,最后打印父亲
// PostOrder(tree);return 0;
}//#include <iostream>
//using namespace std;
//二叉树节点结构
//struct TreeNode {
// int val;
// TreeNode* left;
// TreeNode* right;
// TreeNode(int x) : val(x), left(NULL), right(NULL) {}
//};
//前序遍历
//void preorder(TreeNode* root) {
// if (root == NULL) return;
//
// cout << root->val << " ";
// preorder(root->left);
// preorder(root->right);
//}
//中序遍历
//void inorder(TreeNode* root) {
// if (root == NULL) return;
//
// inorder(root->left);
// cout << root->val << " ";
// inorder(root->right);
//}
//后序遍历
//void postorder(TreeNode* root) {
// if (root == NULL) return;
//
// postorder(root->left);
// postorder(root->right);
// cout << root->val << " ";
//}
//
//int main() {
// // 构建一个简单的二叉树
// TreeNode* root = new TreeNode(1);
// root->left = new TreeNode(2);
// root->right = new TreeNode(3);
// root->left->left = new TreeNode(4);
// root->left->right = new TreeNode(5);
//
// cout << "Preface traversal: ";
// preorder(root);
// cout << endl;
//
// cout << "Middle order traversal: ";
// inorder(root);
// cout << endl;
//
// cout << "Sequential traversal: ";
// postorder(root);
// cout << endl;
//
// return 0;
//}
#include <iostream>
#include <queue>
using namespace std;struct Node {char data;Node* left;Node* right;Node(char value) : data(value), left(nullptr), right(nullptr) {}
};Node* buildTree(const string& s) {if (s.empty()) {return nullptr;}Node* root = new Node(s[0]);queue<Node*> q;q.push(root);int i = 1;while (!q.empty() && i < s.length()) {Node* current = q.front();q.pop();if (s[i] != '#') {current->left = new Node(s[i]);q.push(current->left);}i++;if (i < s.length() && s[i] != '#') {current->right = new Node(s[i]);q.push(current->right);}i++;}return root;
}void inorderTraversal(Node* root) {if (root) {inorderTraversal(root->left);cout << root->data;inorderTraversal(root->right);}
}void postorderTraversal(Node* root) {if (root) {postorderTraversal(root->left);postorderTraversal(root->right);cout << root->data;}
}void levelOrderTraversal(Node* root) {if (!root) {return;}queue<Node*> q;q.push(root);while (!q.empty()) {Node* node = q.front();q.pop();cout << node->data;if (node->left) {q.push(node->left);}if (node->right) {q.push(node->right);}}
}int main() {string input = "abcdefghij";Node* root = buildTree(input);// 中序遍历输出inorderTraversal(root);cout << endl;// 后序遍历输出postorderTraversal(root);cout << endl;// 层序遍历输出levelOrderTraversal(root);cout << endl;return 0;
}