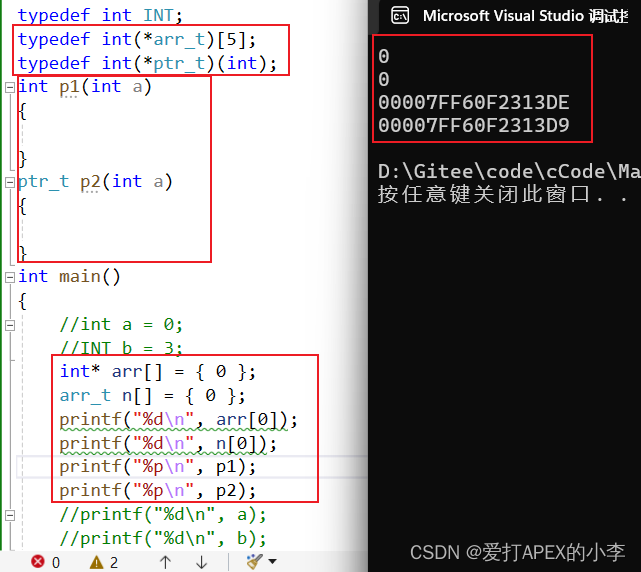
思路:
这道题很容易即可发现就是简单的暴力即可完成题目,我们只需满足所有数的和为偶数即可保证有满足条件的分法,同时也不需要存下每个输入的数据,只需要知道他是偶数还是奇数即可,因为我们只需要偶数个奇数搭配在一块看成是偶数即可,然后对应到上面我们就可以统计一组数据中奇数的个数就不需要多余的计算一个数据和,当奇数个数为0时,情况就是取和不取问题组合情况为2的偶数的个数次方,当奇数个数为奇数时,必不可能有满足条件的情况,当奇数个数为偶数且不为0时,每两个奇数即可配合成一个偶数,奇数的组合数为2的(奇数的个数-1)次方。ps:可以理解为先取出一个奇数,其余奇数为取或者不取那么其中一个子集有奇数个数的奇数另一个必有偶数个数的奇数,只需把这些排列组合(有2的(奇数的个数-1)次方种情况)列出并把取出的奇数放到只有奇数个数的奇数那个子集即可满足条件。
还有说因为奇数得成对出现所以2的n次方除2这个我理解不了我个人想法写到了上面的ps上
核心代码段:

代码:
import java.util.*;public class Main {public static void main (String []args) {int T;Scanner a = new Scanner(System.in);T=a.nextInt();int sum[] = new int[T];int n1=T;while(T-->0){int n;n = a.nextInt();//统计数量int b;//统计奇数和偶数的数目int nj,no;nj=no=0;for(int i=0;i<n;i++) {b=a.nextInt();if(b%2==0) {++no;}else {++nj;}}if(nj%2==0) {//将两个奇数合并为一个偶数,而n个奇数共有n-1种组合然后就是排列组合问题了最多有2的n次方种情况int num =nj+no;if(nj!=0) {num--; }sum[T]=1;
// for(int i=0;i<num;i++) {
// sum[T]=sum[T]*2%1000000007;
// }sum[T]=(int) (Math.pow(2,num)%1000000007);}else {sum[T]=0;} }a.close();for(T=n1-1;T>=0;T--) {System.out.println(sum[T]);}}
}做题反思:
1.蜜汁报错
蓝桥杯代码执行结果为段错误即有越界行为
2.题目有多组数据要输出下面两种都是可以的1.把数据存下来然后一起输出2.算出一个就输出。

fig:情况1
fig:情况2
3.pow返回值为double,先进行(int)会导致精度受损,固要先取余(蓝桥杯很多时候都要先取余输出低位的数值)再数据转换。

eg:
sum[T]=(int) (Math.pow(2,nj)%1000000007);和
sum[T]=(int) Math.pow(2,nj)%1000000007;
的区别在第一个是先取余再转int精度没有丢失,后者是先转int再取余精度在大范围数的时候double变int会精度丢失导致在数值比较大的情况下二者的计算结果有所区别。
上者可以20个结果都对,后者只对4个结果(数据范围小没损失精度)
前者:

后者:
4.区分好continue和break的区别
continue是结束该轮循环,但并没有跳出
break是结束循环即跳出循环

我一开始直接这样导致一直找不到问题,因为就是遇到不满足情况的就跳出循环了,后面的组使用都没有去做,有点逆天了,敲得还是太少了
代码其实十几分钟就敲完了但一直没找出来问题,从晚上7.30到9.20才真正把这道题写完有点ass了
官网一个我觉得写得比较简洁的版本(内核是差不多的我进行了模仿去debug上面的代码而已):
import java.util.*;public class Main {public static void main (String []args) {int T;Scanner a = new Scanner(System.in);T=a.nextInt();long sum[] = new long[T];int n1=T;while(T-->0){int n;n = a.nextInt();//统计数量int b;//统计奇数和偶数的数目int nj,no;nj=no=0;for (int j = 0; j < n; ++j) {int e = a.nextInt();if (e % 2 == 0) ++no;else ++nj;}if (nj % 2 == 0)sum[T] = (int) (Math.pow(2, no) * Math.pow(2, nj == 0 ? 0 : nj - 1) % 1000000007);else sum[T] = 0;}a.close();for(T=n1-1;T>=0;T--) {System.out.println(sum[T]);}}
}