关于数据科学环境的建立,可以参考我的博客:【深耕 Python】Data Science with Python 数据科学(1)环境搭建
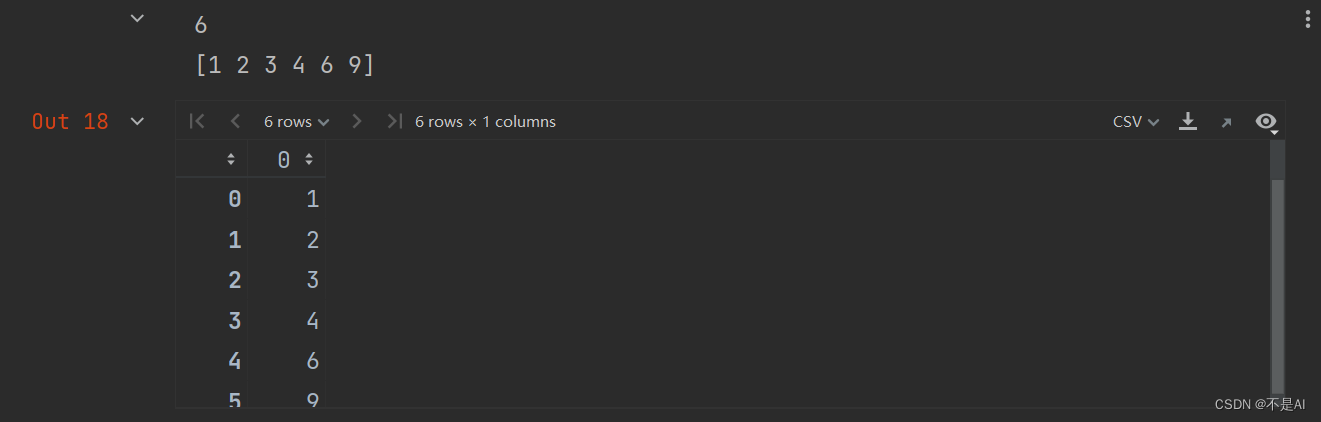
Jupyter代码片段1:简单数组的定义和排序
import numpy as np
np.array([1, 2, 3])
a = np.array([9, 6, 2, 4, 3, 1])
print(len(a))
a.sort()
print(a)
a
输出结果:
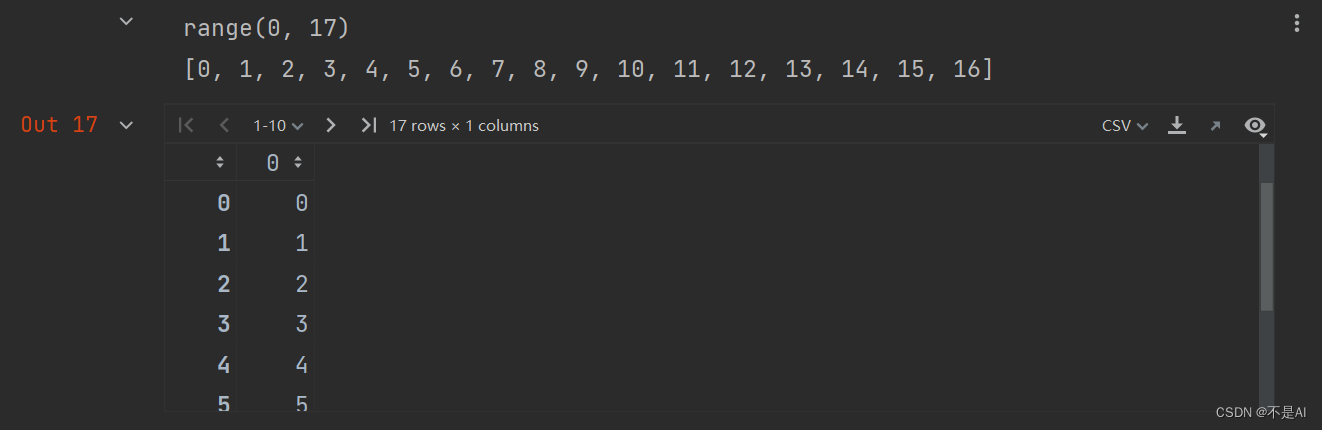
Jupyter代码片段2:范围数组
r = range(17)
print(r)
print(list(r))
a = np.arange(17)
a
输出结果:
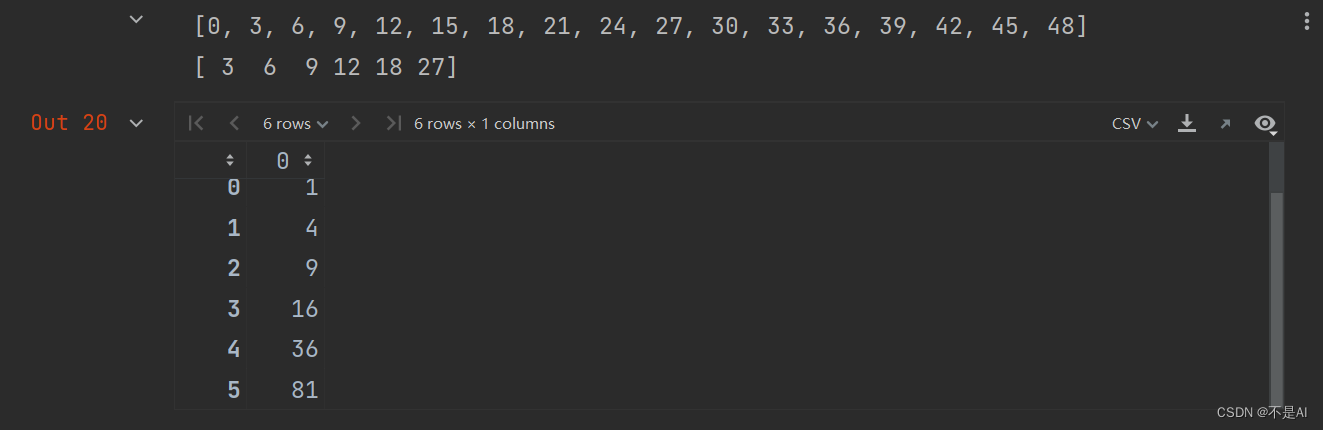
Jupyter代码片段3:对数组的整体操作
print([3 * i for i in r])
print(3 * a)
a ** 2
输出结果:
Jupyter代码片段4:numpy vs 循环用时比较
import timeit
t1 = timeit.timeit("[i ** 2 for i in range(50)]")
t2 = timeit.timeit("import numpy as np; np.arange(50) ** 2")
t1, t2, t1 / t2
输出结果:

优化的底层原理: NumPy将循环语句使用C语言进行优化(Python本即用C语言写成)。
进一步比较2者的速度差异
%%timeit
[i ** 2 for i in range(1000)]
%%timeit
np.arange(1000) ** 2
输出#1:96 µs ± 5.32 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
输出#2:4.04 µs ± 413 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
这样,二者运算速度的区别就一目了然了。
Jupyter代码片段5:高维数组及其子数组
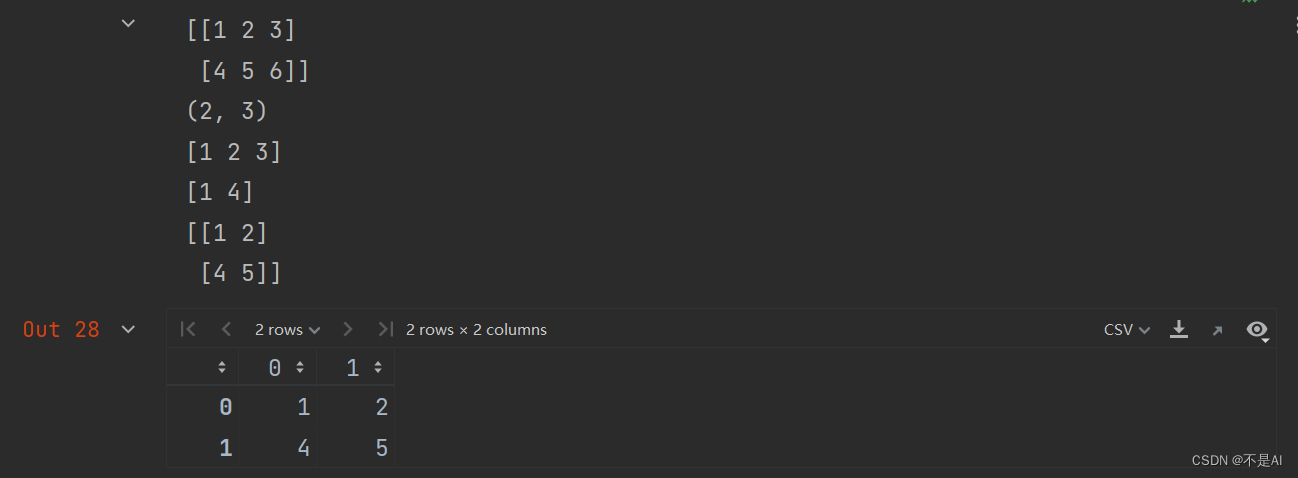
a = np.array([[1, 2, 3], [4, 5, 6]])
print(a)
print(a.shape)
print(a[0, :])
print(a[:, 0])
A = a[0:2, 0:2]
print(A)
A = a[:2, :2]
A
输出结果:
Jupyter代码片段6:二维数组(矩阵)的求逆
Ainv = np.linalg.inv(A)
print(Ainv)
print(A + Ainv)
print(A * Ainv)
print(A @ Ainv)
print(np.matmul(A, Ainv))
输出结果:
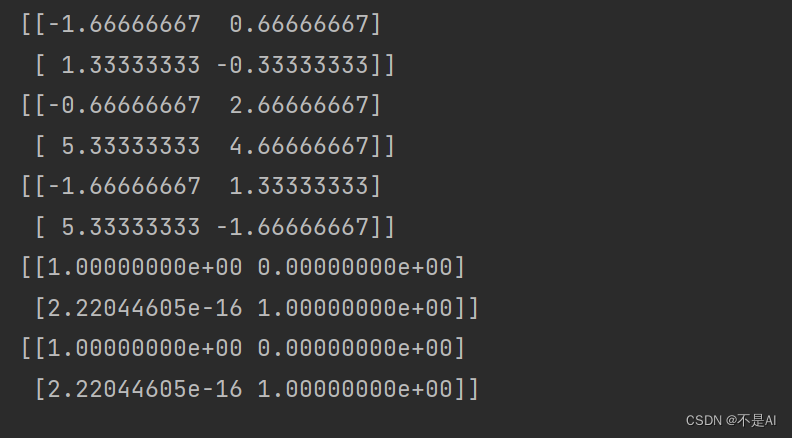
注意: (2阶)单位阵处的浮点误差。
Jupyter代码片段7:数组(矩阵)的重构
a = np.arange(16)
print(a.reshape((2, 8)))
print(a)
b = a.reshape((4, 4))
print(b)
a.reshape((-1, 2))
输出结果:
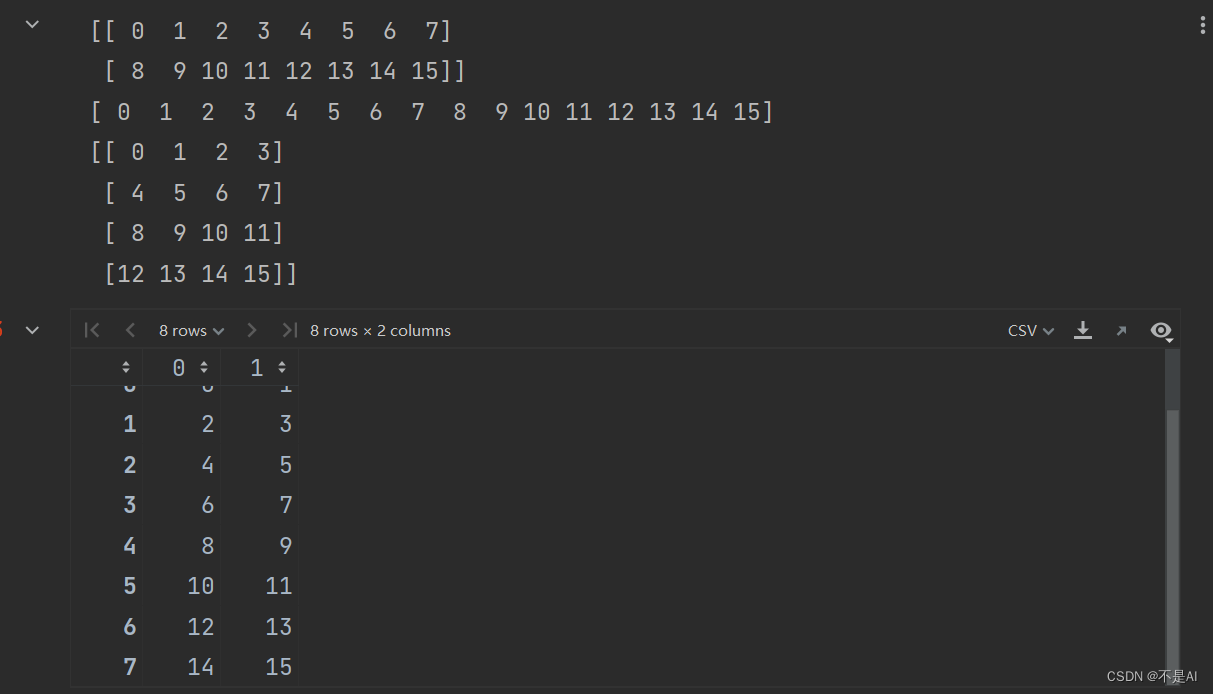
注意(小坑点): 使用a.reshape()并不会改变a本身,需要结合赋值语句来使用。
参考文献 Reference
Learn Enough PYTHON to be Dangerous: Software Development, Flask Web Apps, and Beginning Data Science with Python, Michael Hartl, Pearson, 2023.


![[Python GUI PyQt] PyQt5快速入门](https://img-blog.csdnimg.cn/direct/dfab37ca62e24f6ea4a0eb9dde8626c6.png#pic_center)