目录
A. Stair, Peak, or Neither?
B. Upscaling
C. Clock Conversion
D. Product of Binary Decimals
E. Nearly Shortest Repeating Substring
F. 0, 1, 2, Tree!
G. Shuffling Songs
A. Stair, Peak, or Neither?
直接按照题意模拟即可
void solve(){int a,b,c; cin>>a>>b>>c;if(a<b and b<c ) cout<<"STAIR"<<endl;else if(a<b and b>c) cout<<"PEAK"<<endl;else cout<<"NONE"<<endl;return ;
}B. Upscaling
简单构造,找到题目的性质即可,然后交替输出构造的串
void solve(){cin>>n;string s1,s2;for(int i=1;i<=n;i++){if(i&1){s1.push_back('#');s1.push_back('#');s2.push_back('.');s2.push_back('.');}else{s1.push_back('.');s1.push_back('.');s2.push_back('#');s2.push_back('#');}}for(int i=1;i<=n;i++){if(i&1) cout<<s1<<endl<<s1<<endl;else cout<<s2<<endl<<s2<<endl;}return ;
}C. Clock Conversion
时间模拟按照题意即可
void solve(){int a,b; char op;cin>>a>>op>>b;int ok = a>=12;if(a==0) a=12;if(a>12)a-=12; if(a<10) cout<<0;cout<<a;cout<<":";if(b<10) cout<<0;cout<<b<<' ';cout<<(ok ? "PM" :"AM")<<endl;return ;
}D. Product of Binary Decimals
我们可以发现我们要求的是这个数得要用0101构成的穿的乘积构成,所以我们可以看直接用约数的乘法同时要求这个数是01这样的数即可,注意从大到小的枚举同二进制数取数一样因为有些01数可以由小的01数同其他数的乘积构成
vector<int> s;
void intn(){for(int i=N;i>=10;i--){int x=i;bool ok = true;while(x){int t=x%10;if(t>1) ok = false;x/=10;}if(ok) s.push_back(i);}
}
void solve(){int x; cin>>x; for(auto&v:s) while(x%v==0) x/=v;cout<<(x==1 ? "YES" : "NO")<<endl;return ;
}E. Nearly Shortest Repeating Substring
典型的做法就是使用枚举约数由于这些数只会被约数整除所以直接枚举约数然后检查即可
void solve(){cin>>n;string s; cin>>s;int ans = n;auto check = [&](int i,string now){int t =0;for(int j=0;j<n;j+=i){for(int k=0;k<i;k++){if(s[j+k]!=now[k]) t++;if(t==2) return false;}}return true;};for(int i=1;i<=n/i;i++){if(n%i==0){string now =s.substr(0,i);if(check(i,now)){cout<<i<<endl;return ;}now = s.substr(n-i);if(check(i,now)){cout<<i<<endl;return ;}string x = s.substr(0,n/i);if(check(n/i,x)) ans = min(ans,n/i);x = s.substr(n-n/i);if(check(n/i,x)) ans = min(ans,n/i);}}cout << ans << endl;return ;
}F. 0, 1, 2, Tree!
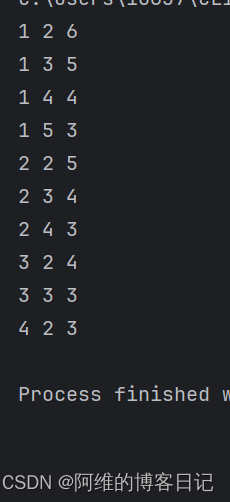
首先我们来看看无解的情况可以发现只有2的度数会给后面带来需要接的点,带来入度,所以最后就是a+1的入度 a+1==c才是有解可以发现如果我们要树的高度低那就是按照满二叉树的方式构造即可,所以我们直接按照先构造2的方式即可,接着处理1的数,1的数量,最后处理没有入度的点
void solve(){int a, b, c;cin >> a >> b >> c;queue<tuple<int, int>> q;q.push({1, 1});int ans = 0;while (a){auto [now, cur] = q.front();q.pop();ans = max(ans, cur);a--;q.push({2 * now, cur + 1});q.push({2 * now + 1, cur + 1});}while (b){auto [now, cur] = q.front();q.pop();ans = max(ans, cur);b--;q.push({2 * now, cur + 1});}if (c != q.size()){cout << -1 << endl;return;}cout << ans << endl;
}G. Shuffling Songs
题目一直在暗示使用的解法,我们考虑dfs或者是状态压缩dp,顺序是可以变化的一个点后面接哪一个点是未知的,也就是我们的哈密顿图,按照题目意思先把可抵达的边建好,然后跑一个状压dp即可
string s[M][2];
void solve(){cin>>n;for(int i=0;i<n;i++){cin>>s[i][0]>>s[i][1];}vector<vector<bool>> g(n,vector<bool>(n,false));for(int i=0;i<n;i++)for(int j=i+1;j<n;j++)if(s[i][0]==s[j][0] or s[i][1]==s[j][1])g[i][j]=g[j][i]=true;vector<vector<bool>> dp(n,vector<bool>(1<<n,false));for(int i=0;i<n;i++) dp[i][1<<i]=true;int ans = 1;for(int state=0;state<(1<<n);state++){for(int i=0;i<n;i++){if(dp[i][state]){for(int j=0;j<n;j++){if(!(state>>j&1) and g[i][j]){dp[j][state|(1<<j)]=true;ans = max(ans,(int)__builtin_popcount((state|(1<<j)))); }}}}} cout<<(n-ans)<<endl;return ;
}