李雅普诺夫函数是一种用于描述动力系统稳定性的数学工具。它在动力系统和控制理论中具有广泛的应用,尤其是在研究非线性系统的稳定性方面。
李雅普诺夫函数通常用于证明动力系统在一些条件下是稳定的。一个李雅普诺夫函数是一个实数值函数,通常表示为 V(x),其中 x 是系统状态的向量。李雅普诺夫函数有以下特点:
- 非负性: 李雅普诺夫函数的值始终大于等于零,即对于所有的状态 x,有 V(x) ≥ 0,并且等号只有在系统的平衡点处取得。
- 非增性: 李雅普诺夫函数的值在系统状态随时间变化时是非增的,即对于系统的任何两个状态 x1 和 x2,有 V(x1) ≥ V(x2)。更具体地,通常是要求李雅普诺夫函数关于系统状态的导数或导数的某种变换(如李普诺夫方程)是负定的。
如果一个李雅普诺夫函数满足上述两个条件之一,那么系统就被认为是稳定的。特别地,如果一个李雅普诺夫函数满足以下条件,那么系统就是渐近稳定的:
存在一个正数常数 α 和一个正数常数 β,使得对于所有的状态 x,有 V(x) ≤ α|x|^2,其中 |x| 表示向量 x 的范数。
李雅普诺夫函数是一种正定的函数,且在系统的平衡点处的导数是负定的。
总之,李雅普诺夫函数是一种有助于分析动力系统稳定性的强大工具,它可以帮助证明系统在一些条件下是稳定的,并提供了在控制系统设计和分析中的重要指导。
让我们以一个简单的非线性系统为例,来演示如何使用李雅普诺夫函数证明系统的稳定性。
考虑如下的非线性系统的微分方程:

我们可以定义一个李雅普诺夫函数 V(x) = x^2。我们来验证这个李雅普诺夫函数是否满足李雅普诺夫定理的条件。
非负性:对于所有的 x,V(x) ≥ 0。这是显然的,因为平方函数的结果始终大于等于零。
非增性:计算李雅普诺夫函数关于时间的导数 dV/dt:
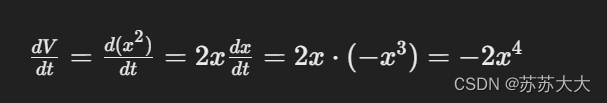
可以看到,对于所有的 x,dV/dt ≤ 0,因此满足了非增性条件。
由于李雅普诺夫函数 V(x) = x^2 满足了李雅普诺夫定理的条件,可以得出结论,系统在原点处是稳定的。这意味着,如果系统的初始状态接近原点,那么系统将趋向于原点,即系统是渐近稳定的。