题目解析

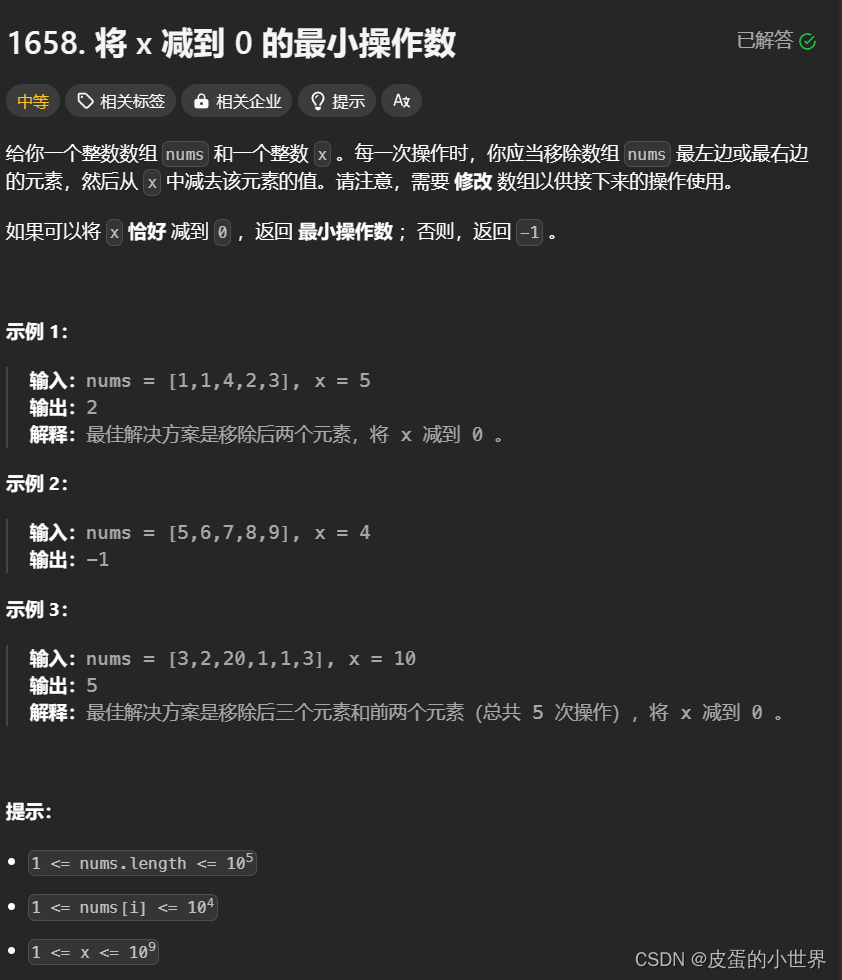
1658. 将 x 减到 0 的最小操作数

---

算法讲解

这道题按照题目要求的话会变得很难，因为不仅需要考虑数字减到0，还需要考虑最小的操作数。正难则反，按照这个思路，我们来解析题目
这道题本质上无非就是在左边寻找一段区间，在右边寻找一段区间，让这两段区间的数字之和等于target，这样自然就可以相减成0。此时我们可以这样想，当我们选完最左边和最右边之后，中间就剩一段连续的区间，我们让这一段连续区间的和 == 整段数组和 - target 即可
所以问题转化为寻找一段最长子数组，使得最长子数组的和等于整段数组和 - target就行

寻找最长子数组我们就是用滑动窗口就是了

class Solution {
public:int minOperations(vector<int>& nums, int target) {//这道题转化为寻找一段最长子数组的和 == sum - targetint sum = 0;for(auto k : nums) sum += k;int x = sum - target;if(x < 0)return -1;//按照要求寻找最长子数组int left = 0, right = 0;int n = nums.size();int temp_sum = 0;int len = INT_MIN;while(right < n){temp_sum += nums[right];while(temp_sum > x){temp_sum -= nums[left++];}if(temp_sum == x){len = max(len, right - left + 1);}right++;}if(len == INT_MIN)return -1;return n - len;}
};

下面的这一段代码是由顺序的，我们一进循环就需要+=当前的数值，但是+=完成之后它是有可能超过目标值的，所以就需要循环判断进而移动左窗口，判断完成我们就需要进行当前temp_sum 是否等于 目标值的判断，只有当以上两个判断都没有的时候才进行right++

 temp_sum += nums[right];while(temp_sum > x){temp_sum -= nums[left++];}if(temp_sum == x){len = max(len, right - left + 1);}right++;

---