题目描述： 

动物王国中有三类动物 A,B,C这三类动物的食物链构成了有趣的环形。

A 吃 B，B 吃 C，C吃 A。

现有 N 个动物，以 1∼N 编号。

每个动物都是 A,B,C 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 N个动物所构成的食物链关系进行描述：

第一种说法是 1 X Y，表示 X和 Y 是同类。

第二种说法是 2 X Y，表示 X 吃 Y。

此人对 N个动物，用上述两种说法，一句接一句地说出 K 句话，这 K 句话有的是真的，有的是假的。

当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

1. 当前的话与前面的某些真的话冲突，就是假话；
2. 当前的话中 X 或 Y比 N 大，就是假话；
3. 当前的话表示 X 吃 X，就是假话。

你的任务是根据给定的 N 和 K 句话，输出假话的总数。

输入格式

第一行是两个整数 N和 K，以一个空格分隔。

以下 K 行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中 D 表示说法的种类。

若 D=1，则表示 X 和 Y 是同类。

若 D=2，则表示 X 吃 Y。

输出格式

只有一个整数，表示假话的数目。

数据范围

1≤N≤50000,
0≤K≤1000000

输入样例：

100 7
1 101 1 
2 1 2
2 2 3 
2 3 3 
1 1 3 
2 3 1 
1 5 5

输出样例：

3

---

思路： 

首先我们要知道并查集中每一个集合以树的形式进行存储
此题需要我们维护的信息是d[](节点边的权值)。

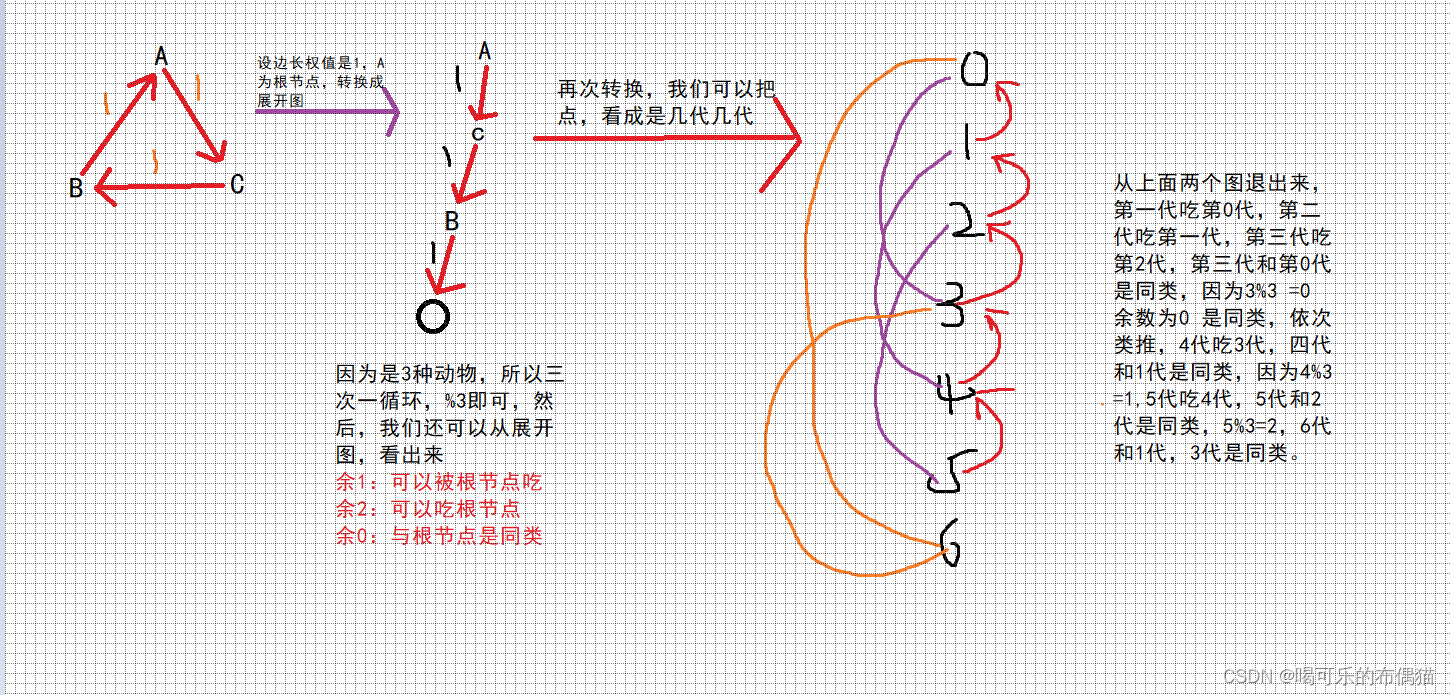
 从此图中我们还可以发现，此图为一个有向图且成一个环形状，可以推出3个动物一循环

所以我们只需要知道两个动物的关系，放到集合中，集合中所有动物的关系，我们是一定可以退出来的。

---

我们思考一个位置，如果推出来的呢？ 

例如：x与y是同类，y被z吃，我们是不是可以推出来x也被z吃呢

再比如：x吃y， y吃z，通过上面我们画的有向图，是不是也能推出来z吃x呢。因为是一个环形有向图吗，所以一定可以推出来的这里就不画图了，类比上面的图。

---

那么我们如何确定一个集合里面的动物之间关系呢？ 

我们只需要找出此点与根节点之间的关系即可。

例如：如下图

---

下面我们来看一下代码。 

---

 AC代码：

//首先我们要知道并查集中每一个集合以树的形式进行存储
//此题需要我们维护的信息是d[](节点边的权值)。
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 5e4+10;
int n,m;
//p[]->存出父亲节点，d[]->i到用来存储到根节点的距离
//刚开始自己一个类所以d[]都是0
int p[N],d[N];//路径压缩，顺势求出每个点到根节点的距离
int find(int x)
{//如果不是根节点就执行if(p[x] != x){//用来存储一下根节点,为了不影响后面求x到根节点的值int t = find(p[x]);//累加求出x（该点）到根节点的值d[x] += d[p[x]];p[x] = t;//指向根节点，路径压缩成功}return p[x];//返回父亲节点
}int main()
{int res = 0;//计算假的个数scanf("%d%d", &n, &m);//刚开始自己为单独一个集合for(int i=1;i<=n;i++) p[i] = i;while (m -- ){int t,x,y;scanf("%d%d%d",&t,&x,&y);//当前的话中 X或 Y比 N大，就是假话 if(x > n || y > n)res ++;else{   //分别求一下两个动物的根节点，为了后面确认关系int px = find(x),py = find(y);//同类if(t==1){//如果在一个根节点下，要保证d[x] % 3 == d[y] % 3 ---> (d[x] - d[y])%3==0if(px == py && (d[x] - d[y])%3) res++;//如果不在一个根节点下else if(px!=py){//不妨让x编号根节点合并到y编号下根节点下。也就是py是px的父亲节点p[px] = py;//d[x] + ? - d[y] = 0 -- > ? = d[y] - d[x];d[px] = d[y] - d[x];}}else//被吃的关系{//如果在一个根节点下，x吃y，第0代被第1代吃，第一代被第二代吃，第三代吃第二代//可以知道x是比y到根节点距离多1的，所以(d[x] - d[y] - 1)%3 = 0;if(px == py && (d[x] - d[y] - 1) % 3) res++;else if(py!=px){p[px] = py;//d[x] + ? - 1 - d[y] = 0 ---> ? = d[y] + 1 - d[x];d[px] = d[y] + 1 - d[x];}}}}printf("%d",res);return 0;
}

---

上述代码大家可能会疑问，d都初始化为0了，那无论d[x]加多少次d[p[x]]，结果都是0啊 ？ 

d[px] = d[y] + 1 - d[x];

我们可以看到此代码，在我们插入两个动物关系的时候，这里已经有+1的操作了，所以我们不用担心这个问题。

---

 第二个有问题的地方可能是find函数那里

int find( int x ) {
if( p[x] != x ) {
// int t = find( p[x] );
d[x] += d[p[x]];
p[x] = find( p[x] );
}
return p[x];
}

为什么不可以上面那么写，一定要像下面那么写呢？

int find( int x ) {
if( p[x] != x ) {
int t = find( p[x] );
d[x] += d[p[x]];
p[x] = t;
}
return p[x];
}

这里推荐大家手动模拟一遍，然后看一下两者的区别，第一种只能去求出到父亲节点的距离，并不能够达到累加求到根节点的距离，相比之下，第二种可以。 

---

对于这段代码图解：

---

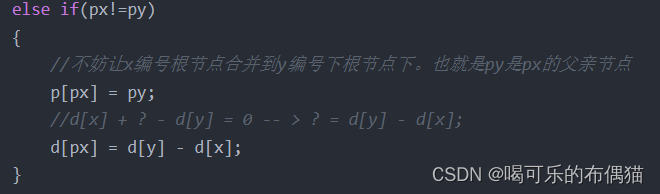
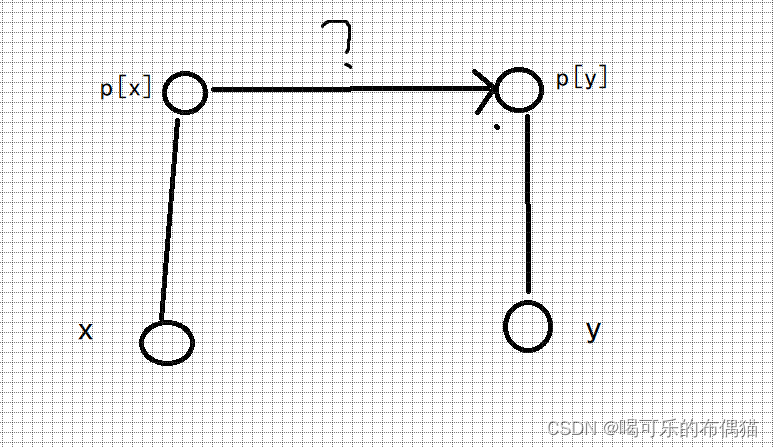
对于这段代码图解：

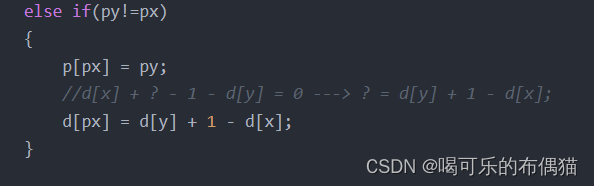
 注意X到根的距离比Y多1，因为是X吃Y，可以根据上面图理解一下

---

对于find函数里的递归如下：

此图来源于acwing题解中一位大佬的图解，原图在：AcWing 240. 食物链---数组d的真正含义以及find()函数调用过程 - AcWing

---

欢迎不会的小伙伴留言~