资料:https://www.zhihu.com/question/47559783/answer/2988744371
https://www.zhihu.com/question/47559783
https://blog.csdn.net/seek97/article/details/120012667
一、基本思想
-
在对一个状态值进行估计的时候,如果想测量值更准,很自然的一个想法就是用多个传感器去对同一个状态进行测量,然后取平均值。
x 估计 = ( x 传感器 1 + x 传感器 2 ) 2 x_{估计} = \frac{(x_{传感器1} + x_{传感器2})}{2} x估计=2(x传感器1+x传感器2) -
如果不同的传感器之间准确度有区别,那么对不同传感器的测量值取加权值就很有必要了。
x 估计 = α ∗ x 传感器 1 + ( 1 − α ) ∗ x 传感器 2 x_{估计} = \alpha*x_{传感器1} + (1-\alpha)*x_{传感器2} x估计=α∗x传感器1+(1−α)∗x传感器2 -
如果我们并没有多余的对状态直接测量的传感器,但是有物理模型。基于上一时刻的状态估计值对当前时刻进行预测,也可以作为一个“传感器”的测量值。
x 估计 = α ∗ x 预测 + ( 1 − α ) ∗ x 传感器 x_{估计} = \alpha*x_{预测} + (1-\alpha)*x_{传感器} x估计=α∗x预测+(1−α)∗x传感器 -
至此,卡尔曼滤波的基本思想就给出了,通过预测值和测量值的加权和作为当前状态的估计。那么问题的关键就变成了如何设置权重才能让这个估计是最优估计。
二、如何获得权重
1、直观理解

-
上面这种图中曲线是数值的概率分布情况(横轴是数值,纵轴是概率,积分是1),粉色曲线代表预测值,绿色代表测量值,蓝色是我们想得到的估计值。
-
针对正态分布的数据,如果方差越大,概率就约集中,也说明数值越可信。以方差为权重,并考虑和为1,则有如下公式:
x 估计 = σ 传感器 2 ( σ 传感器 2 + σ 预测 2 ) ∗ x 预测 + σ 预测 2 ( σ 传感器 2 + σ 预测 2 ) ∗ x 传感器 x_{估计} = \frac{{\sigma_{传感器}}^2}{({\sigma_{传感器}}^2+{\sigma_{预测}}^2)}*x_{预测} + \frac{{\sigma_{预测}}^2}{({\sigma_{传感器}}^2+{\sigma_{预测}}^2)}*x_{传感器} x估计=(σ传感器2+σ预测2)σ传感器2∗x预测+(σ传感器2+σ预测2)σ预测2∗x传感器 -
如何从数学推导的角度印证上面这个公式呢?
2、数学推导
- 设 α \alpha α是最佳的权重
x 估计 = α ∗ x 预测 + ( 1 − α ) ∗ x 传感器 x_{估计} = \alpha*x_{预测} + (1-\alpha)*x_{传感器} x估计=α∗x预测+(1−α)∗x传感器 - 基于概率公式进行推导
σ 估计 2 = α 2 ∗ σ 预测 2 + ( 1 − α ) 2 ∗ σ 传感器 2 {\sigma_{估计}}^2 = {\alpha}^2*{\sigma_{预测}}^2+{(1-\alpha)}^2*{\sigma_{传感器}}^2 σ估计2=α2∗σ预测2+(1−α)2∗σ传感器2 - 基于导数=0计算 σ 估计 2 {\sigma_{估计}}^2 σ估计2的最小值
σ 估计 = σ 传感器 2 ( σ 传感器 2 + σ 预测 2 ) \sigma_{估计} = \frac{{\sigma_{传感器}}^2}{({\sigma_{传感器}}^2+{\sigma_{预测}}^2)} σ估计=(σ传感器2+σ预测2)σ传感器2
3、迭代计算
- 卡尔曼滤波有五个公式,相互联系组成了迭代更新的公式
(1)预测状态的更新公式
x t , t − 1 = a ∗ x ^ t − 1 , t − 1 + b + q x_{t,t-1} = a* {\hat x}_{t-1,t-1}+b+q xt,t−1=a∗x^t−1,t−1+b+q
- x t , t − 1 x_{t,t-1} xt,t−1是这一次的预测状态值, x ^ t − 1 , t − 1 {\hat x}_{t-1,t-1} x^t−1,t−1是上一次的估计值。a是状态转移,b是控制量,q是先验的模型噪声(很多没有这一项)
(2)预测状态协方差的更新公式
σ t , t − 1 = a 2 ∗ σ x ^ t − 1 , t − 1 + σ q {\sigma}_{t,t-1} = a^2* {\sigma}_{{\hat x}_{t-1,t-1}}+{\sigma}_q σt,t−1=a2∗σx^t−1,t−1+σq
- 系统模型的方差是变化的,系统的方差来源于两部分,一部分是上一时刻的估计值导致的误差,我们利用模型计算当前的状态时,只能使用上一次的估计值代替实际值。另一部分就是模型本身的误差,模型本身也会存在着系统误差。
(3)卡尔曼增益的更新公式
k t = σ x , t − 1 σ x , t − 1 + σ z k_t = \frac{{\sigma}_{x,t-1}}{{\sigma}_{x,t-1}+{\sigma}_{z}} kt=σx,t−1+σzσx,t−1
- 这就是上面推导出的对估计值方差的最佳估计,在这种情况下估计值应该方差最小
- 传感器的方差一般是固定的,可以认为是先验知道的。预测值的方差在上一步已经获得。
(4)估计状态的更新公式
x ^ t = ( 1 − k t ) ∗ x t − 1 + k t ∗ z t {\hat x}_{t} = (1-k_t)*x_{t-1}+k_t*z_t x^t=(1−kt)∗xt−1+kt∗zt
(5)估计状态协方差的更新公式
- 根据公式4就可以获得协方差:
σ x ^ t = ( 1 − k t ) 2 ∗ σ x t − 1 + k t 2 ∗ σ z , t {\sigma}_{{\hat x}_{t}} = (1-k_t)^2*{\sigma}_{x_{t-1}}+k_t^2*{\sigma}_{z,t} σx^t=(1−kt)2∗σxt−1+kt2∗σz,t - 再把公式3代入:

(6)扩展到多维情况
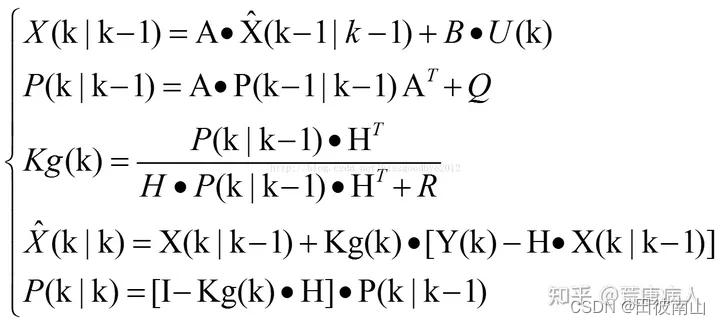
- H是观测值到状态值的转换矩阵
- Q是模型噪声,R是观测噪声。越小表示越相信对应的值,如果为0就代表完全相信(没有噪声当然可以完全相信了)
三、例子
(1)chatgpt生成的一维python代码
import numpy as np
import matplotlib.pyplot as pltdef kalman_filter(data, Q, R):# 初始化x = 0P = 1result = []for z in data:# 预测x_pred = x #没有控制量P_pred = P + Q# 更新K = P_pred / (P_pred + R)x = x_pred + K * (z - x_pred)P = (1 - K) * P_predresult.append(x)return result# 生成随机数据
np.random.seed(42)
data = np.random.normal(0, 1, 50) # 生成50个均值为0,方差为1的随机数# 添加噪声
data_noisy = data + np.random.normal(0, 0.8, 50) # 添加方差为0.8的高斯噪声# 卡尔曼滤波
Q = 0.1
R = 0.5
filtered_data = kalman_filter(data_noisy, Q, R)# 绘图
plt.figure(figsize=(12, 6))
plt.plot(data, label='True Data', color='blue')
plt.plot(data_noisy, label='Noisy Data', color='red', alpha=0.7)
plt.plot(filtered_data, label='Filtered Data', color='green', linestyle='--')
plt.legend()
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Kalman Filter Example')
plt.show()