4.3.2 旋转的万花筒
【问题】 万花简的初始形状如图4-4(a)所示,其中的圆圈代表万花简的闪烁点,每旋转一次万花简形状就演变一次,演变的规则是在末端再生出同样的形状,如图4-4(b)和图4-4(c)所示,求第n次旋转后有多少个闪烁点?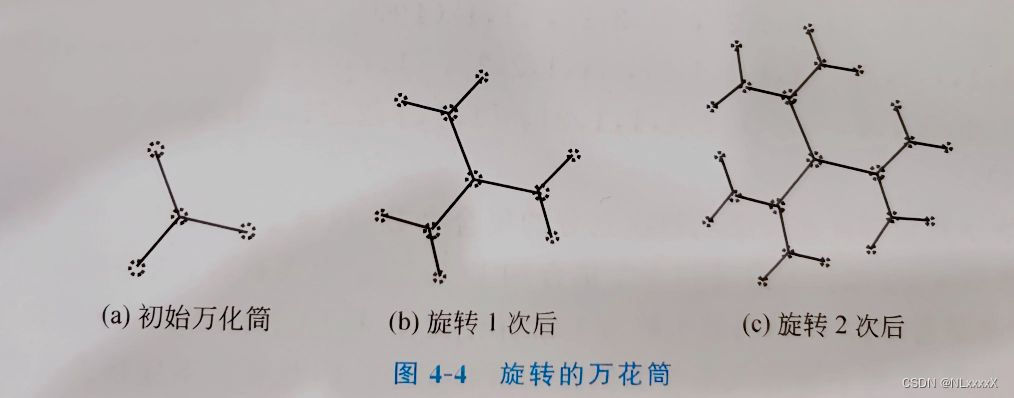
【想法】 仔细观察万花简的演变过程,初始时有4个闪烁点,第1次旋转在初始闪烁点的基础上,每个分支端点又多了2个闪烁点。设Sn表示第n次旋转的闪烁点个数,每次旋转都是在上一次旋转的每个分支端点又多了2个闪烁点,初始时有3个分支端点,第1次旋转有3×2个分支端点,每次旋转分支端点都会翻倍,得到如下递推关系式: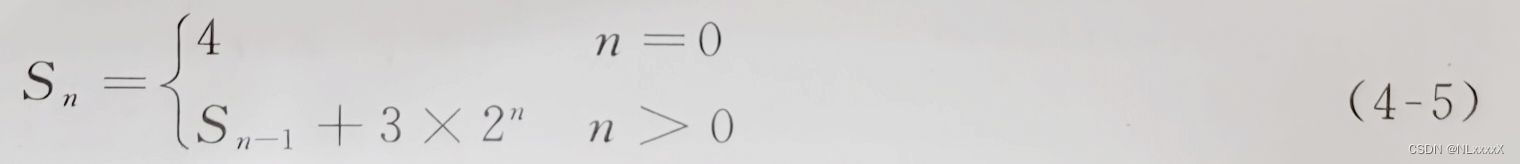
【算法实现】 设函数Kale实现旋转的万花筒,变量lamps 表示上一次旋转后的闪烁点,变量 addLamp 表示当次旋转闪烁点的增量,程序如下。
#include <iostream>
using namespace std;
int Kale(int n)
{
int i, lamps = 4, addLamp = 3;
for (i = 1; i <= n; i++)
{
addLamp *= 2;
lamps += addLamp;
}
return lamps;
}
int main( )
{
int n;
cout<<"请输入旋转次数:";
cin>>n;
cout<<"第"<<n<<"次闪烁点为"<<Kale(n)<<endl;
return 0;
}
【算法分析】 显然,算法Kale的时间复杂度为O(n)。
4.4.1 整数划分
【问题】 对于一个大于2的整数n,要求仅使用2的若干次幂的整数集合进行划分,使得集合中所有整数之和等于n,问可以有多少种划分?
【想法】列出一些整数的划分,寻找递推关系式:
2:(1, 1),(2)(2种)
3:(1, 1, 1),(1,2)(2种)
4:(1, 1, 1, 1),(1, 1, 2),(2, 2),(4)(4种)
5:(1, 1, 1.1, 1),(1, 1, 1, 2),(1, 2, 2),(1, 4)(4种)
6:(1,1, 1,1, 1,1), (1,1,1,1,2),(1,1,2,2),(1,1,4),(2, 2,2),(2,4)(6种)
7.(1,1,1,1,1,1,1),(1,1, 1,1,1,2),(1,1,1,2,2),(1,1,1,4),(1,2, 2,2),(1, 2,4)(6种)
令d,表示对整数n进行2的幂次划分的集合个数,观察上述划分实例,当n为奇数时,只需在整数n-1划分集合的每一个集合加上1;当n为偶数时,在整数n-1划分集合中的每一个集合加上1,得到最小数为1的所有划分,再将整数n/2划分集合的每一个集合中的元素翻倍,得到所有元素均为偶数的所有划分。因此有如下递推关系式:
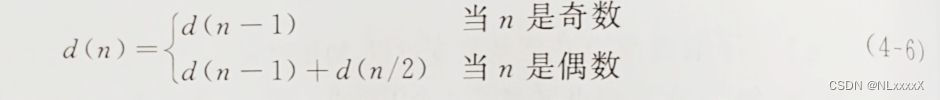
【算法实现】 设函数 Devide 实现集合划分,数组 d[n+1]表示对整数n进行2的幂次划分的集合数,程序如下,
#include <iostream>
using namespace std;
int Devide(int n)
{
int i, d[n+1] = {0};
d[1] = 1; d[2] = 2;
for (i = 3; i <= n; i++)
if (i % 2 != 0) d[i] = d[i-1];
else d[i] = d[i-1] + d[i/2];
return d[n];
}
int main( )
{
int n;
cout << "请输入一个整数:";
cin >> n;
int result = Devide(n);
// 输出划分的结果
cout << "对 " << n << " 进行划分的结果为:" << result << endl;
return 0;
}