资料：
桥式起重机防摇定位控制系统开发，毕江涛
基于输入整形的桥式起重机货物摆动控制策略研究，王冰清
基于输入整形技术的门座起重机吊重摆动控制研究，王云飞
基于变增益 PID 控制的起重机防摇摆设计与仿真，郭瀛舟
https://blog.csdn.net/wh_STUDY/article/details/126403817
https://zhuanlan.zhihu.com/p/402291172

一、动力学模型

1、时域模型

（1）非线性起重机

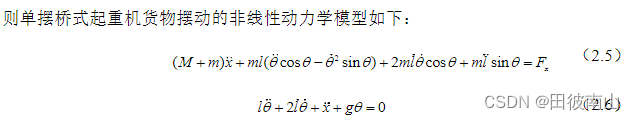
（2）线性化起重机

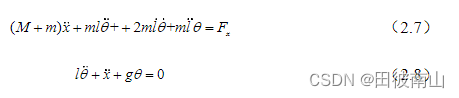
• 这个2.8少写了一个$2\dot{l}\dot{\theta }$

2、频域模型

(1) 输入加速度，输出摆角

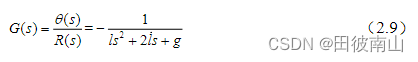
可以化为下面的标准型

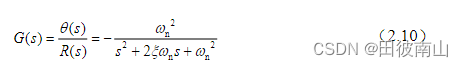
（2）输入速度，输出摆角

$$G(s)=\frac{\theta (s)}{v(s)}=\frac{s}{l{s}^2+2\dot{l}s+g}$$

二、输入整形算法

1、基本思想

• 这个思想很简单，考虑无阻尼的情况，当一个激励让系统产生震荡后，只要滞后半个周期再次给出一个等幅的激励，两个振荡的激励就会相互抵消。（这里只讨论ZV）
• 上面说的是无阻尼的情况，但是无阻尼是不可能的，在第一个振荡产生后的半个周期内，系统会因为阻尼的存在而趋于收敛，所以第二个激励要比第一个激励小。至于激励小多少，就是跟阻尼本身有关了，不过实际应用中有很多是阻尼较小的情况，其实可以忽视阻尼，直接给两个等幅的激励。下面这个图是考虑阻尼的情况。

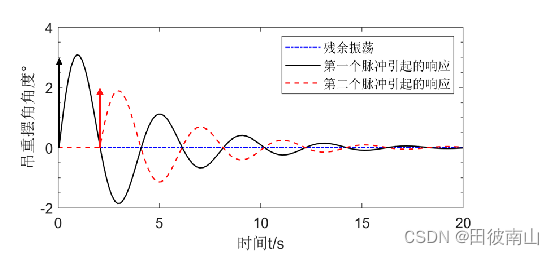
• 上面图中提到的残余振动是指当第二个激励给出后振荡的情况。

2、实现方法

（1）关键参数计算

• 可以想到如果想设计这个算法，我们只需要知道两个振荡的振幅如何分配以及两者的间隔即可。
  
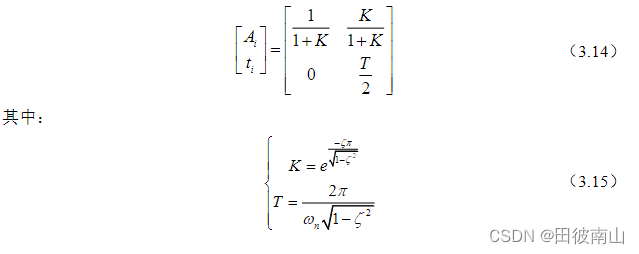
• 上面这个是ZV的设计公式，其中有几个点需要注意。首先，两次振幅之和为1，意味不会减低原本的幅度。
• T的计算公式就是一般二阶系统的计算公式，而第二次激励发出的时间就是周期的一半
• K的值受阻尼影响，当阻尼为0时，也就是等幅振荡时，两个激励幅度相等，并为总幅度的一半
• 注意两次信号都是在之前状态下再一次激励，所以整形后的信号是阶梯状的，这个可以看下面频域的图
• 下面是时域的表达式
  

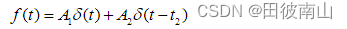
（2）整形后信号计算

• 如果是相对固定的阶跃信号，时域计算就可以了。但是如果输入信号会变化，会出现不同的信号组合，那么频域计算就简单一点了。
• 周期和幅度依旧使用上面的结果，下面进行频域的实现
• 下面这个是频域的计算形式，输入信号和整形器进行卷积，输入整形器就是两个时间和幅度不同的冲击信号的叠加
  
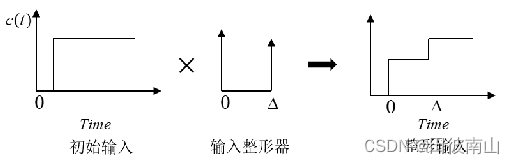
• 注意这个整体状态，一个阶跃信号进行整形后变成了一个分两次进行阶跃的信号，最终幅度与原来一致。
• 这里使用两个冲击信号组成输入整形器，主要是冲击信号具有显象性，在特定的时间会呈现之前信号的一定幅度。
• 频域计算过程
  $$Au(t)\ast (A_1\delta (t)+A_2\delta (t-a))=整形后的信号$$
  拉普拉斯变换：
  $$\frac{A}{s}\times A_1+\frac{A}{s}\times A_2{e}^{-as}=整形后的信号$$
  拉普拉斯逆变换：
  $$L^{-1}(\frac{A}{s}\times A_1+\frac{A}{s}\times A_2{e}^{-as})=A{A}_1\delta (t)+A{A}_2\delta (t-a)$$
  *最后这步是延迟性质

3、计算例子

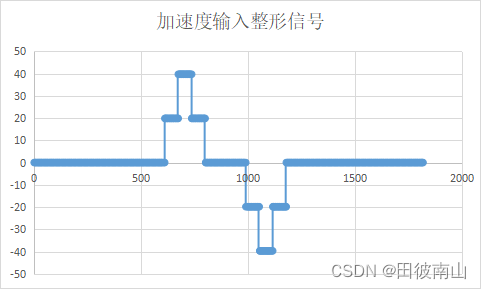
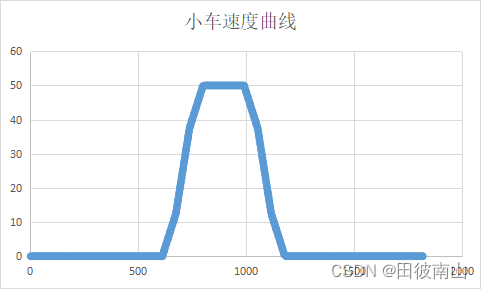
• 在实际应用中，因为涉及到阶跃的情况，对于电机来说加速度的阶跃是比速度的阶跃要容易的，所以一般对加速度进行输入整形，但是最终要通过加速度计算速度，再由电机控制速度。

• 这里是跑了一个具体的工况先加速，到达一定速度后匀速一小段，再减速到0。工况要求加速度出现了四次改变，所以有四次输入整形，最终是八次变化。