归并排序
归并排序是利用归并的思想实现的排序方法,该算法采用经典的分治策略(分治法将问题分成一些小的问题然后递归求解,而治的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
分而治之
可以看到这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。
过程:左部分排好序,右部分排好序,利用merge过程让左右整体有序(merge过程:谁小拷贝谁,直到左右两部分所有的数字耗尽)
归并排序算法有两个基本的操作,一个是分,也就是把原数组划分成两个子数组的过程。另一个是治,它将两个有序数组合并成一个更大的有序数组。
- 将待排序的线性表不断地切分成若干个子表,直到每个子表只包含一个元素,这时,可以认为只包含一个元素的子表是有序表。
- 将子表两两合并,每合并一次,就会产生一个新的且更长的有序表,重复这一步骤,直到最后只剩下一个子表,这个子表就是排好序的线性表。
分阶段
可以理解为就是递归拆分子序列的过程,利用二分法
递归深度为log2n。
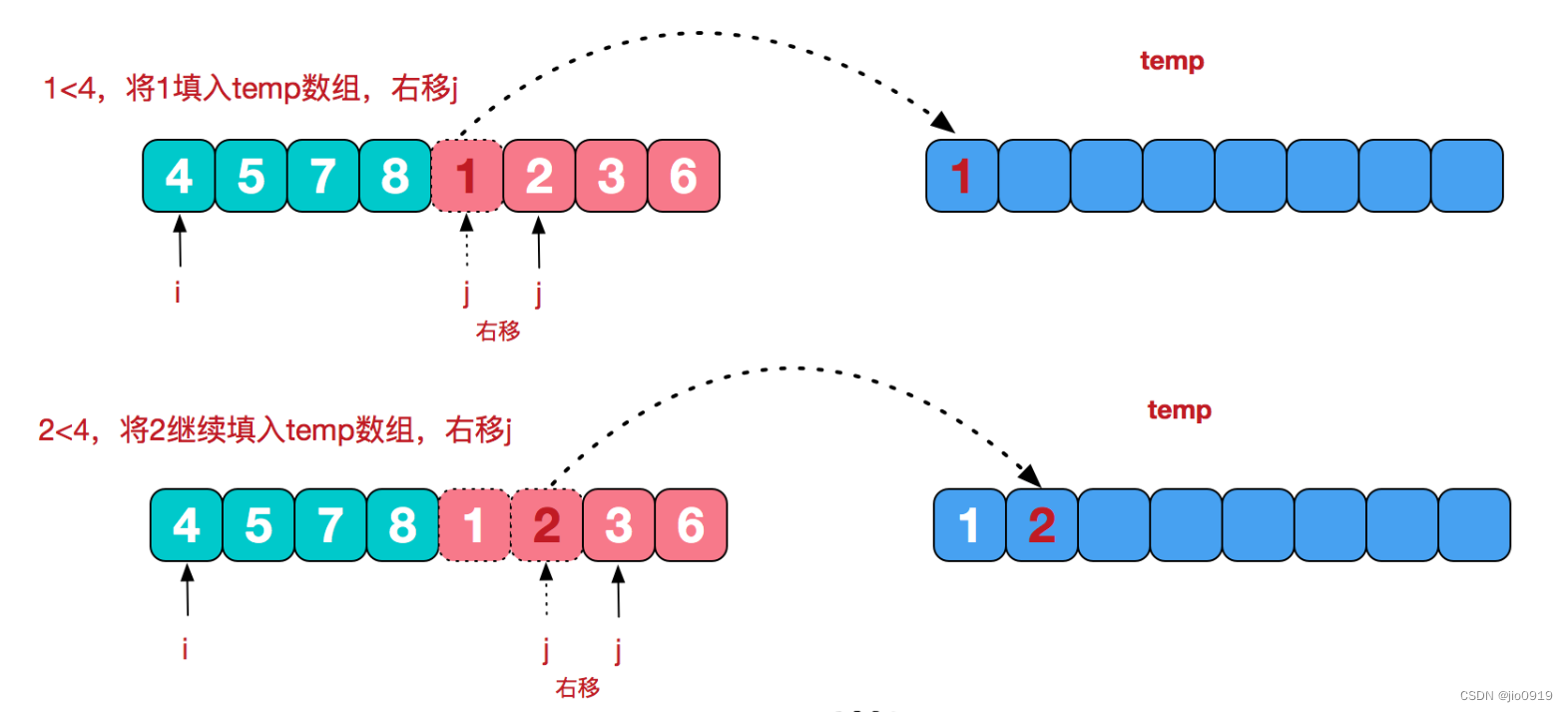
合并两个有序数组流程
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。

代码:
# include <stdio.h>int arr[100];
inr help[100];int n;void mergesort(int l, int r)
{if (l == r)return;int m = (l+r) / 2;mergesort(l, m);mergesort(m+1, r);merge(l, m, r); //让左右整体有序
}//让 l 到 r 变 有序
//把[l, m] 和 [m+1, r]进行合并
void merge(int l, int m, int r)
{int i = l;int a = l;int b = m+1; while (a <= m && b <=r){if (arr[a] <= arr[b]){help[i] = arr[a];a = a + 1;}else{help[i] = arr[b];b = b + 1;}i = i + 1;}//左侧指针,右侧指针,必有一个越界,另一个不越界while (a <= m){help[i] = a;i = i + 1;a = a + 1;} while (b <= r){help[i] = b;i = i + 1;b = b + 1;} for (int i=l; i<=r; ++i){arr[i] = help[i];}
}int main()
{scanf("%d", &n);for (int i=0; i<n; ++i)scanf("%d", &arr[i]);mergesort(0, n-1);}
归并分治

问题一
 本题发现
本题发现
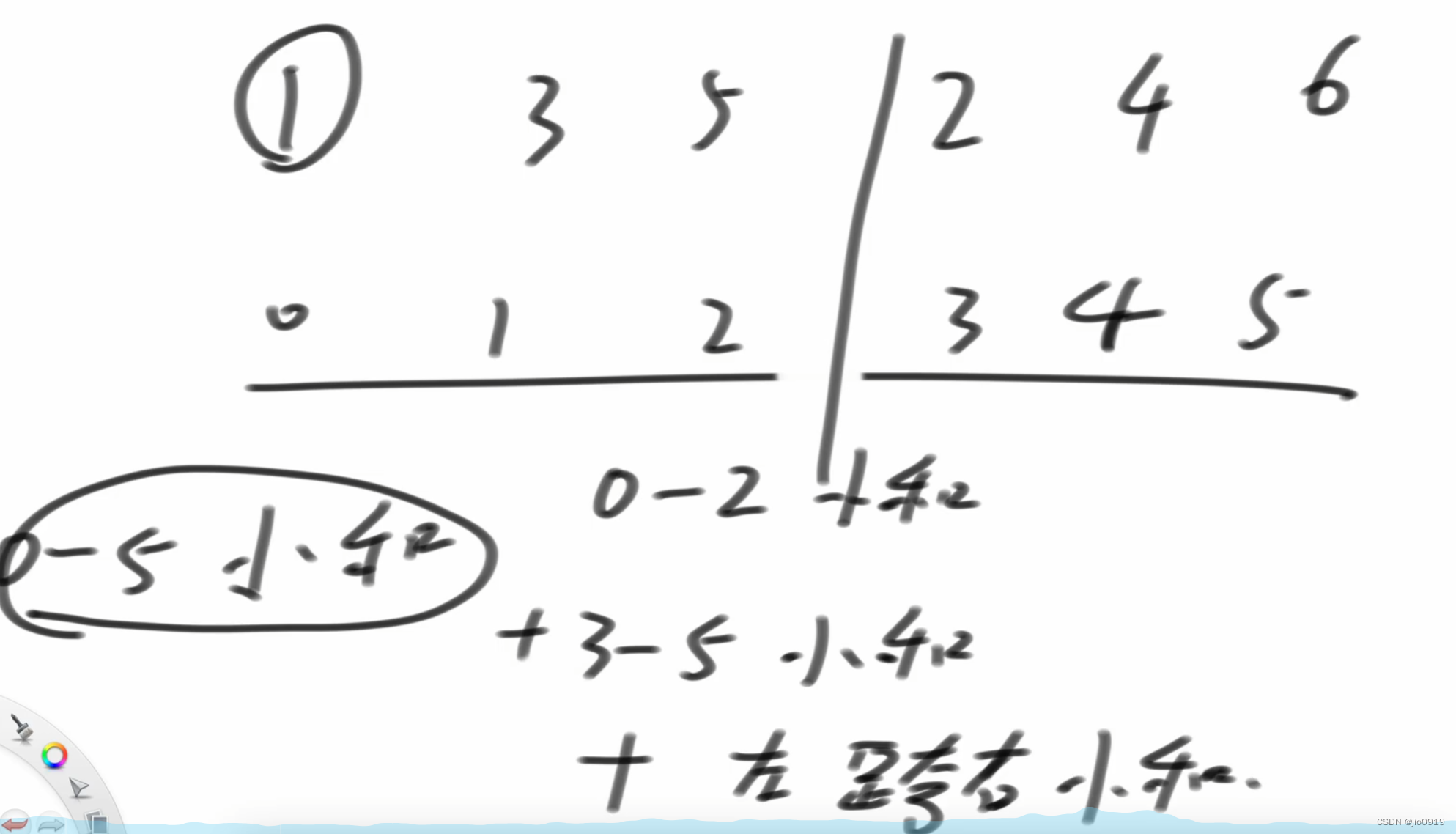
符合第一个原理
在计算跨越左右产生的答案时,我们发现如果左、右各有序,则会提高计算便利性
因此就可以考虑归并分治
代码:
# include <stdio.h>int arr[100];
int help[100];int n;int sum(int l, int r)
{if (l == r)return 0;int m = (l + r) / 2;return sum(l, m) + sum(m+1, r) + merge(l, m, r);
}int merge(int l, int m, int r)
{int ans = 0;int j = l;int sum = 0;for (int i=m+1; i<r; ++i){while (j <= m && arr[i] >= arr[j]){sum = sum + arr[j];j = j + 1;}ans = ans + sum;}int i = l;int a = l;int b = m + 1;while (a <= m && b <=r){if (arr[a] <= arr[b]){help[i] = arr[a];a = a + 1;}else{help[i] = arr[b];b = b + 1;}i = i + 1;}//左侧指针,右侧指针,必有一个越界,另一个不越界while (a <= m){help[i] = a;i = i + 1;a = a + 1;} while (b <= r){help[i] = b;i = i + 1;b = b + 1;} for (int i=l; i<=r; ++i){arr[i] = help[i];}
}int main()
{scanf("%d", &n);for (int i=0; i<n; ++i)scanf("%d", &arr[i]);int ans = sum(0, n-1);}问题二

符合第一个原理
在计算跨越左右产生的答案时,我们发现如果左、右各有序,则会提高计算便利性
因此就可以考虑归并分治
代码:
# include <stdio.h>int arr[100];
int help[100];int n;int cmp(int l, int r)
{if (l == r)return 0;int m = (l+r) / 2;return cmp(l, m) + cmp(m+1, r) + merge(l, m, r);
}int merge(int l, int m, int r)
{int j = l;int q = m+1;int sum = 0;int ans = 0;for (int i=l; i<=m; ++i){while (q <= r && arr[i] > arr[q] * 2){q = q + 1;}ans = ans + (q - m - 1) - i;}int x = l;int a = l;int b = m + 1;while (a <= m && b <=r){if (arr[a] <= arr[b]){help[x] = arr[a];a = a + 1;}else{help[x] = arr[b];b = b + 1;}x = x + 1;}//左侧指针,右侧指针,必有一个越界,另一个不越界while (a <= m){help[x] = a;x = x + 1;a = a + 1;} while (b <= r){help[x] = b;x = x + 1;b = b + 1;} for (int i=l; i<=r; ++i){arr[i] = help[i];}return ans;
}int main()
{scanf("%d", &n);for (int i=0; i<n; ++i)scanf("%d", &arr[i]);}