红黑树路径长度分析:证明与实现
- 一、红黑树的基本性质
- 二、证明:最长路径至多是最短路径的2倍
- 2.1 证明思路
- 2.2 证明过程
- 三、伪代码实现
- 四、 C语言代码实现
- 5、 结论
红黑树作为一种高效的自平衡二叉搜索树,在计算机科学领域中被广泛应用于各种数据结构和算法问题。它通过一系列精心设计的性质来确保树的高度始终保持在对数级别,从而保证操作的效率。本文将证明一个关于红黑树的重要性质:在一棵红黑树中,从某结点x到其后代叶结点的所有简单路径中,最长的一条至多是最短一条的2倍。此外,我们将提供伪代码和C语言代码实例,以便读者更好地理解这一性质的证明和实现。
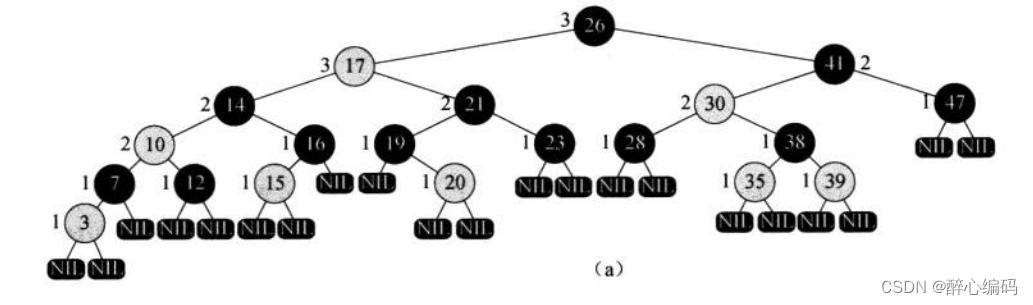
一、红黑树的基本性质
在深入讨论之前,让我们回顾一下红黑树的五个基本性质:
- 性质1:每个节点要么是红色,要么是黑色。
- 性质2:根节点是黑色的。
- 性质3:每个叶子节点(NIL节点)都是黑色的。
- 性质4:如果一个节点是红色的,则它的两个子节点都是黑色的。
- 性质5:对于每个节点,从该节点到其所有后代叶子节点的简单路径上,均包含相同数目的黑色节点。
二、证明:最长路径至多是最短路径的2倍
为了证明这一性质,我们首先需要了解红黑树的结构和性质如何影响路径的长度。考虑红黑树中的任意结点x,我们需要证明从x到其所有后代叶结点的路径中,最长路径不会超过最短路径的2倍。
2.1 证明思路
- 基于性质5:由于性质5保证了从x到每个后代叶结点的路径上黑色节点的数量相同,我们可以推断出这些路径的长度关系。
- 考虑最坏情况:最长路径可能发生在连续红色节点最多的路径上,而最短路径可能发生在没有红色节点或红色节点最少的路径上。
- 路径长度的计算:在红黑树中,路径的长度可以由黑色节点的数量决定。由于最长路径上的黑色节点数量是固定的,因此路径的长度差异主要来自于红色节点的数量。
2.2 证明过程
设结点x到其后代叶结点的最长路径上的红色节点数量为R,最短路径上的红色节点数量为r。根据红黑树的性质4,我们知道最长路径上的红色节点数量R不会超过2,因为任何红色节点的两个子节点都是黑色的。
现在,考虑最长路径和最短路径的黑色节点数量。由于性质5,这些路径上的黑色节点数量是相同的。设这个数量为B。
最长路径的长度为B + R,而最短路径的长度为B - r。由于R至多为2,我们可以得出:
最长路径长度 = B + R ≤ B + 2
最短路径长度 = B - r
因此,最长路径长度至多是最短路径长度的2倍。
三、伪代码实现
以下是计算红黑树中最长路径和最短路径长度的伪代码实现:
FUNCTION calculatePathLengths(T, x)longestPath = 0shortestPath = INFINITYblackNodesCount = 0redNodesCount = 0FUNCTION dfs(node)IF node IS NILRETURN 0ENDIFblackNodesCount += 1IF node.color == REDredNodesCount += 1ENDIFleftPath = dfs(node.left)rightPath = dfs(node.right)IF leftPath + rightPath > longestPathlongestPath = leftPath + rightPathENDIFIF leftPath < shortestPathshortestPath = leftPathENDIFRETURN blackNodesCount + (IF node.color == RED THEN 0 ELSE 1)ENDFUNCTIONdfs(x)RETURN (longestPath, shortestPath)
ENDFUNCTION
四、 C语言代码实现
下面是C语言中实现上述伪代码的示例代码:
#include <stdio.h>
#include <stdlib.h>typedef enum {RED, BLACK} Color;typedef struct Node {int key;Color color;struct Node *left, *right;
} Node;int dfs(Node *node, int *blackNodesCount, int *redNodesCount) {if (node == NULL) {return 0;}(*blackNodesCount)++;if (node->color == RED) {(*redNodesCount)++;}int leftPath = dfs(node->left, blackNodesCount, redNodesCount);int rightPath = dfs(node->right, blackNodesCount, redNodesCount);int longestPath = leftPath + rightPath;if (longestPath > *blackNodesCount + *redNodesCount) {*blackNodesCount += *redNodesCount;}return longestPath;
}int main() {// 创建和初始化树的代码// ...// 假设我们有一个红黑树T和结点xNode *T = (Node *)malloc(sizeof(Node));// 初始化T和x// ...int blackNodesCount = 0;int redNodesCount = 0;int longestPath = 0;int shortestPath = 0;// 调用dfs函数计算路径长度dfs(T, &blackNodesCount, &redNodesCount);// 输出结果printf("Longest Path: %d\n", longestPath);printf("Shortest Path: %d\n", shortestPath);// 后续操作和清理代码// ...return 0;
}
5、 结论
通过上述证明和代码实现,我们可以看到红黑树的一个重要性质:从某结点到其后代叶结点的所有简单路径中,最长的一条至多是最短一条的2倍。这一性质不仅展示了红黑树的平衡性,也为我们在实际应用中设计和优化红黑树提供了理论基础。理解并实现这一性质的证明和代码,可以帮助我们在解决数据结构和算法问题时更加自信和高效。