Abstract

提出了一种新颖的元学习方法，用于自动剪枝非常深的神经网络。首先训练一个称为PruningNet的元网络，该网络能够针对目标网络生成权重参数，以生成任何剪枝结构。使用简单的随机结构抽样方法来训练PruningNet。然后，应用进化过程来搜索表现良好的剪枝网络。这种搜索非常高效，因为权重是由经过训练的PruningNet直接生成的，在搜索时不需要任何微调。通过为目标网络训练单个PruningNet，可以在几乎没有人为参与的情况下，在不同约束条件下搜索各种剪枝网络。与最先进的剪枝方法相比，在MobileNet V1/V2和ResNet上展示了更优越的性能。

github仓库

1 Introduction

典型的剪枝方法包含三个阶段：训练大型过度参数化网络、剪枝不太重要的权重或通道、微调或重新训练剪枝后的网络。第二阶段是关键。它通常执行迭代分层剪枝和快速微调或权重重建以保持精度。

最近的一项研究发现，无论是否继承原始网络中的权重，剪枝网络都可以达到相同的精度。这一发现表明，通道剪枝的本质是找到良好的剪枝结构——逐层通道数。

然而，详尽地寻找最佳剪枝结构在计算上是令人望而却步的。考虑一个$10$层的网络，每层包含$32$个通道。分层通道数的可能组合可以是 $32^{10}$。

受到最近的神经架构搜索（NAS）的启发，特别是One-Shot模型，以及HyperNetwork中的权重预测机制，本文提出训练一个PruningNet，它可以为所有候选修剪网络结构生成权重，这样就可以通过评估验证数据的准确性来搜索性能良好的结构，这是非常高效的。

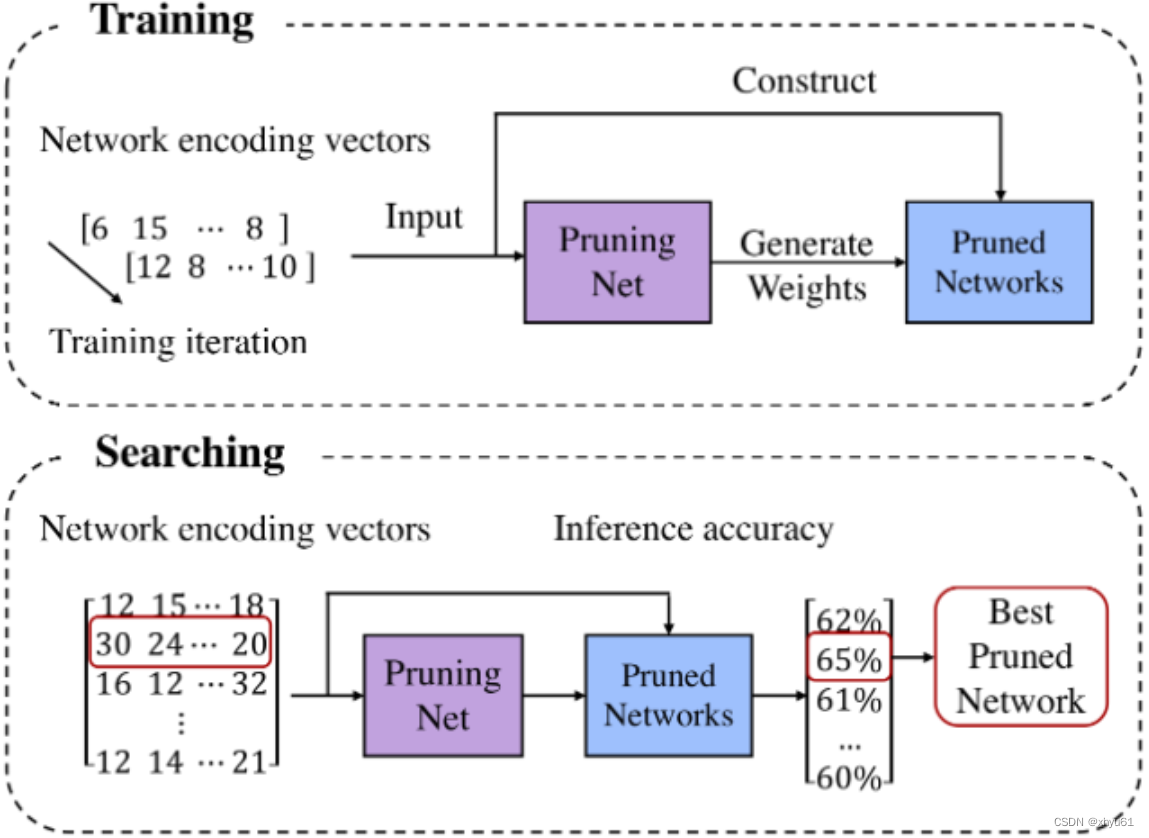
图1：MetaPruning有两步。1)训练PruningNet。每次迭代，随机生成一个网络编码向量(network encoding vectors)，并对应生成剪枝后的网络(Pruned Network)。PruningNet将网络编码向量作为输入并生成Pruned Network的权重。2)搜索最佳的Pruned Network。通过改变网络编码向量构建了许多剪枝网络，并使用PrunedNet预测的权重来评估它们在验证数据上的优劣。搜索时无需进行微调。

为了训练PruningNet，使用随机结构采样。PruningNet使用相应的网络编码向量生成剪枝网络的权重，即每层的通道数。通过随机输入不同的网络编码向量，PruningNet逐渐学习为各种修剪结构生成权重。训练结束后，通过进化搜索方法来搜索性能良好的剪枝网络，该方法可以灵活地结合计算FLOP或硬件延迟等各种约束。此外，通过确定每一层或每一阶段的通道来直接搜索最佳剪枝网络，可以在捷径中剪枝通道而无需额外的努力，这在以前的通道剪枝解决方案中很少得到解决。
本文将这个方法称为MetaPruning。

本文贡献分为4点：

• 提出了一种元学习方法，MetaPruning，用于通道剪枝。方法的核心是学习一个元网络Pruning Net，它为各种修建结构生成权重。通过单个经过训练的PruningNet，可以在不同约束下搜索各种剪枝网络。
• 与传统的剪枝方法相比，MetaPruning跳出繁琐的超参数调整，能够根据所需的指标直接进行优化。
• 与其他AutoML方法相比，MetaPruning可以轻松地在搜索所需结构时强制实施约束，而无需手动调整强化学习超参数。
• 元学习能够毫不费力地修剪类似ResNet结构的快捷连接中的通道，这并非易事，因为快捷连接中的通道影响不止一层。

3 Methodology

本节引入了元学习方法，用于自动修剪深度神经网络中的通道，修剪后的网络可以轻松满足各种约束。

公式化通道剪枝问题：
$$(c_1,c_2,\cdots ,c_l{)}^{\ast }=\underset{c_1,c_2,\cdots ,c_l}{\mathrm{argmin}}\mathcal{L}(\mathcal{A}(c_1,c_2,\cdots ,c_l;w)\text{s.t.}\mathcal{C}<\text{constraint}$$
$\mathcal{A}$为剪枝前的网络。尝试找到剪枝后的网络，从第一层到第$l$层具有$(c_1,c_2,\cdots ,c_l)$个通道，使得权重被训练后具有最小的损失，同时使成本$\mathcal{C}$满足约束（FLOP或延迟）。
为了实现这一目标，提出构建一个PruningNet，一种元网络，可以仅通过评估验证数据来快速获得所有潜在修剪网络结构的优点。然后可以应用任何搜索方法，即本文中的进化算法，来搜索最佳剪枝网络。

3.1 PruningNet training

通道剪枝并非易事，因为通道中的分层依赖性使得剪枝一个通道可能会显着影响后续层，从而降低整体精度。以前的方法试图将通道剪枝问题分解为逐层剪枝不重要通道的子问题或添加稀疏正则化。

考虑整体剪枝网络结构来执行信道剪枝任务，有利于寻找信道剪枝的最优解，并且可以解决捷径剪枝问题。然而，获得最佳剪枝网络并不简单，考虑到一个10层且每层包含32个通道的小型网络，可能的剪枝网络结构的组合是巨大的。

受最近工作的启发，该工作表明剪枝留下的权重与剪枝后的网络结构相比并不重要，这鼓励直接找到最佳剪枝后的网络结构。从这个意义上说，可以直接预测最佳剪枝网络，而无需迭代确定重要的权重过滤器。为了实现这一目标，构建了一个元网络 PruningNet，为各种修剪后的网络结构提供合理的权重，以对其性能进行排名。

PruningNet是一个元网络，它以网络编码向量$(c_1,c_2,\cdots ,c_l)$作为输入，并输出剪枝网络的权重：
$$W=PruningNet(c_1,c_2,\cdots ,c_l)$$

图2：提出的PruningNet随机训练方法。在每次迭代中，随机化一个网络编码向量。 PruningNet通过将向量作为输入来生成权重。剪枝网络是根据向量构建的。裁剪 PruningNet生成的权重以匹配 Pruned Network中的输入和输出通道。通过在每次迭代中改变网络编码向量，PruningNet可以学习为各种修剪网络生成不同的权重。

PruningNet块由两个全连接层组成。在前向传递中，PruningNet将网络编码向量（即每层的通道数）作为输入，并生成权重矩阵。同时，构造剪枝网络，每层的输出通道宽度等于网络编码向量中的元素。生成的权重矩阵被裁剪以匹配剪枝网络中输入和输出通道的数量，如图2所示。给定一批输入图像，可以使用生成的权重计算剪枝网络的损失。

在向后传递中，不是更新Pruned Networks中的权重，而是计算PruningNet中权重的梯度。由于PruningNet中全连接层的输出与Pruned Network中前一个卷积层的输出之间的重塑操作以及卷积操作也是可微的，因此可以轻松计算PruningNet中权重的梯度由链式法则。 PruningNet是端到端可训练的。PruningNet与Pruned Network连接的详细结构如图3所示。

图3：(a)PruningNet与Pruned Network连接的网络结构。PruningNet和Pruned Network通过网络编码向量和小批量图像的输入进行联合训练。(b)对PruningNet块生成的权重矩阵进行重塑和裁剪操作。

为了训练PruningNet，提出了随机结构采样。在训练阶段，网络编码向量是通过在每次迭代时随机选择每层的通道数来生成的。通过不同的网络编码，构建不同的Pruned Network，并由PruningNet提供相应的权重。通过使用不同的编码向量进行随机训练，PruningNet学会预测各种不同修剪网络的合理权重。

3.2 Pruned-Network search

PruningNet训练完成后，可以通过将网络编码输入PruningNet，生成相应的权重并对验证数据进行评估来获得每个潜在剪枝网络的准确率。
由于网络编码向量数量巨大，无法一一列举。为了找出约束下高精度的剪枝网络，使用进化搜索，它能够轻松地合并任何软或硬约束。

在MetaPruning中使用的进化算法中，每个剪枝网络在每一层中都用一个通道数向量进行编码，称为剪枝网络的基因。在硬约束下，首先随机选择一些基因，通过评估得到相应剪枝网络的准确率。然后选择准确度最高的前k个基因来产生突变和交叉的新基因。突变是通过随机改变基因中一定比例的元素来进行的。交叉意味着随机重组两个亲本基因中的基因以产生后代。可以通过消除不合格的基因来轻松地强制执行约束。通过进一步重复top k选择过程和新基因生成过程多次迭代，可以获得满足约束的基因，同时达到最高的准确率。具体算法参见Algorithm 1。

Algorithm 1: Evolutionary Search Algorithm

超参数：人口规模$\mathcal{P}$，突变数$\mathcal{M}$，交叉数$\mathcal{S}$，最大迭代次数$\mathcal{N}$。
输入：PruningNet，限制$\mathcal{C}$。
输出：具有最高准确率的基因${\mathcal{G}}_{\text{top}}$。

$g_0=\text{Random}(\mathcal{P}),\text{s.t.}\mathcal{C};$
${\mathcal{G}}_{\text{topK}}=\varnothing$
for $i=0:\mathcal{N}$ do:

{ G i , accuracy } = Inference ( P r u n i n g N e t ( G i ) ) \{\mathcal{G}_i,\text{accuracy}\}=\text{Inference}(PruningNet(\mathcal{G}_i)) {Gi​,accuracy}=Inference(PruningNet(Gi​))
G topK , accuracy topK = TopK ( { G i , accuracy } ) \mathcal{G}_{\text{topK}}, \text{accuracy}_\text{topK}=\text{TopK}(\{\mathcal{G}_i,\text{accuracy}\}) GtopK​,accuracytopK​=TopK({Gi​,accuracy})
${\mathcal{G}}_{\text{mutation}}=\text{Mutation}({\mathcal{G}}_{\text{topK}},\mathcal{M}),\text{s.t.}\mathcal{C}$
${\mathcal{G}}_{\text{crossover}}=\text{Crossover}({\mathcal{G}}_{\text{topK}},\mathcal{S}),\text{s.t.}\mathcal{C}$
${\mathcal{G}}_i={\mathcal{G}}_{\text{mutation}}+{\mathcal{G}}_{\text{crossover}}$
end for
G top1 , accuracy top1 = Top1 ( { G N , accuracy } ) \mathcal{G}_\text{top1},\text{accuracy}_\text{top1}=\text{Top1}(\{\mathcal{G}_\mathcal{N},\text{accuracy}\}) Gtop1​,accuracytop1​=Top1({GN​,accuracy})
return ${\mathcal{G}}_{\text{top1}}$

4 Experimental Results

在本节中，展示了提出的MetaPruning方法的有效性。首先解释实验设置并介绍如何在MobileNet V1、V2和 ResNet上应用MetaPruning，它可以很容易地推广到其他网络结构。其次，将的结果与统一的剪枝基线以及最先进的通道剪枝方法进行比较。第三，可视化通过MetaPruning获得的修剪网络。最后，进行消融研究以阐述方法中权重预测的效果。

4.1 Experiment settings

所提出的MetaPruning非常有效。因此在ImageNet 2012分类数据集上进行所有实验是可行的。

MetaPruning方法由两个阶段组成。在第一阶段，PruningNet是通过随机结构采样从头开始训练的，与正常训练网络一样需要$\frac{1}{4}$数量的epochs。进一步延长PruningNet训练在获得的Pruned Net中几乎没有产生最终的精度增益。在第二阶段，使用进化搜索算法来找到最佳的修剪网络。通过PruningNet预测所有PrunedNet的权重，搜索时无需微调或重新训练，这使得进化搜索非常高效。在8个Nvidia 1080Ti GPU上推断PrunedNet只需几秒钟。然后从头开始训练从搜索中获得的最佳PrunedNet。对于两个阶段的训练过程，使用标准数据增强策略来处理输入图像。对于MobileNets的实验，采用与相同的训练方案；对于ResNet，采用中的训练方案。所有实验的输入图像分辨率均设置为224×224。

在训练时，将原始训练图像分成子验证数据集和子训练数据集。子验证数据集包含从训练图像中随机选择的50000张图像，每个1000类别有50张图像，而剩余的图像则组成子训练数据集。在子训练数据集上训练PruningNet，并在搜索阶段评估剪枝网络在子验证数据集上的性能。在搜索时，使用20000张子训练图像重新计算BatchNorm层中的运行均值和运行方差，以正确推断剪枝网络的性能，这仅需几秒钟时间。在获得最佳剪枝网络后，将剪枝网络从头开始在原始训练数据集上进行训练，并在测试数据集上进行评估。