MATLAB实现数值求解高阶常微分方程组-编程知识

MATLAB实现数值求解高阶常微分方程组

一、高阶常微分方程组

高阶常微分方程是指包含多个高阶常微分方程的系统。这些方程通常涉及多个未知函数及其高阶导数。解决高阶常微分方程组通常比解决单个高阶常微分方程更为复杂，因为需要同时考虑多个方程和多个未知函数之间的关系。

一般来说，解决高阶常微分方程组的方法包括：

降阶法：通过引入新的变量或函数，将高阶方程转化为低阶方程或一阶方程组。这种方法可以简化问题，使其更容易解决。
分离变量法：如果方程组中的某些项可以分离出来，使得方程变得更容易解决，那么可以使用分离变量法。
特征线法：对于某些特定类型的高阶偏微分方程组，可以使用特征线法来求解。
数值方法：对于无法找到解析解的情况，可以使用数值方法来近似求解。这包括有限差分法、有限元法、谱方法等。

二、四阶龙格库塔方法

在本文中着重介绍利用四阶龙格库塔方法求解常微分方程，四阶龙格库塔方法（RK4）是是一种常用的数值积分方法，用于求解常微分方程的数值解。它是龙格库塔法的一种升级版，具有更高的精度。该方法通过计算多个斜率，并通过加权平均的方式得到下一个因变量的值。虽然四阶龙格库塔方法能提供较为精确的数值解，但由于需要计算多个斜率，所以计算量相对较大。

四阶龙格库塔法的原理基于泰勒级数展开，通过不断迭代来逼近微分方程的解。其基本思想是将微分方程中的导数用差分来代替，然后通过一系列计算步骤来逼近真实解。

具体来说，四阶龙格库塔方法的核心是求解导数值，并在指定的区间内取多个导数值进行加权平均，以得到更为精确的解。其求解式一般形式如下：

$y_{n+1} = y_n + \frac{h}{6} (k_1 + 2k_2 + 2k_3 + k_4)\\ k_1 = f(t_n)\\ k_2 = f(t_n + \frac{h}{2})\\ k_3 = f(t_n + \frac{h}{2})\\ k_4 = f(t_n + h)\\$

其中， $y_n$ 和 $y_{n+1}$ 分别是第n步和第n+1步的函数值，h是步长， $k_1, k_2, k_3, k_4$ 是在不同点上的斜率近似值。

总的来说，四阶龙格库塔方法是一种有效的数值积分方法，能够用于求解常微分方程的数值解，尤其适用于那些难以用数学方法直接求解的复杂方程。

三、MATLAB代码求解

clear;clc;clf;
tspan = linspace(0,0.08,100000);%自变量
initial = [0;29;1500];%初始值
[t,y] = ode45(@ode2,tspan,initial);%龙格——库塔法
figure(1)
yyaxis left
h1 = plot(t, y(:,1),'-','Color','b','LineWidth',1.5);
hold on
h2 = plot(t, y(:,2),'--','Color','b','LineWidth',1.5);
yyaxis right
h3 = plot(t, y(:,3),'-','Color','r','LineWidth',1.5);
hx = xlabel('Time (s)');
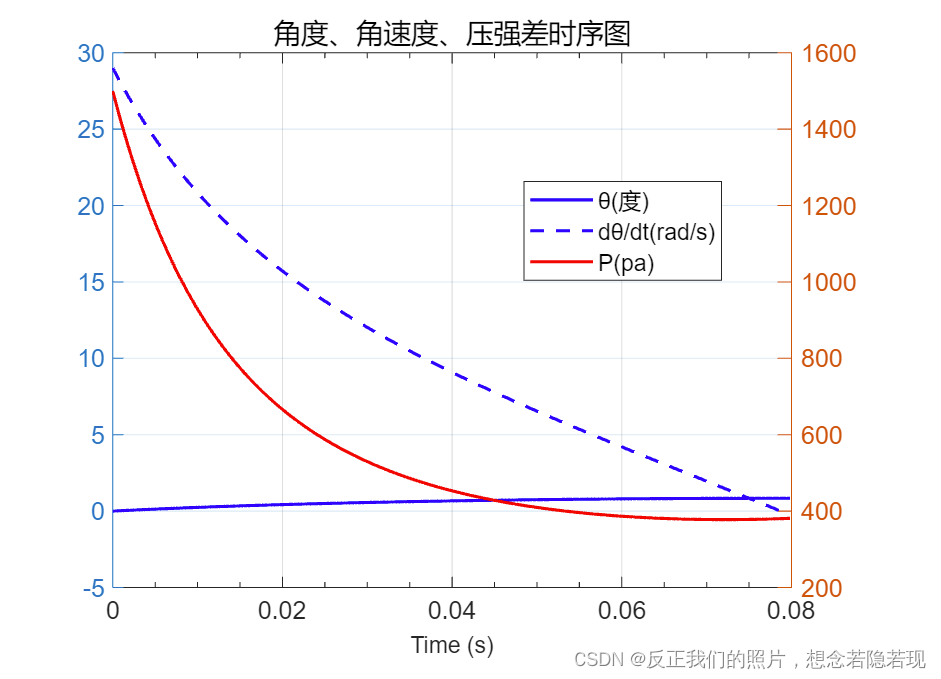
title('角度、角速度、压强差时序图');
set(gca,'Box','on',...'XGrid','on','YGrid','on',...'XMinorTick','on','TickLength',[0.02,0.02],...'TickDir','in');
hl = legend([h1,h2,h3],["θ(度)","dθ/dt(rad/s)","P(pa)"],"Position", [0.61266,0.57863,0.2,0.15]);
set(gca,'FontName','Helvetica','FontSize',12);
set([hl,hx],'FontName','Helvetica','FontSize',11);
function dtheta = ode2(t,theta)
%dtheta(2)的系数
a1 = 414.5/3.727;
a2 = -2.94/3.727;
%dtheta(3)的系数
b1 = 1100/1.47;
b2 = -2.94/1.47;
dtheta = zeros(3,1);
dtheta(1) = theta(2);
dtheta(2) = a1*cos(theta(1))+a2*theta(3);
dtheta(3) = b1+b2*theta(3)*cos(theta(1))*theta(2);
end

利用双y轴将数值求解可视化，蓝色实线和虚线对应左边坐标轴，红色实线对应右边坐标轴：