Toyota Programming Contest 2024#4（AtCoder Beginner Contest 348）（A~D）-编程知识

A - Penalty Kick

i,1~N。如果 i 是 3 的倍数输出x，否则输出o

#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define all(x) x.begin(),x.end()
#define EX exit(0)
#define fr first
#define se second
//#define endl '\n'
using namespace std;
using ll=long long;void solve(){int n;cin>>n;per(i,1,n){if(i%3==0){cout<<"x";}else cout<<"o";}
}signed main(){ios::sync_with_stdio(false),cin.tie(nullptr);int t=1;while(t--)solve();return 0;
}

B - Farthest Point

给你 N 个点，问你 1~N 每个点，各自的最远点是哪个，两点距离计算公式如下图所示。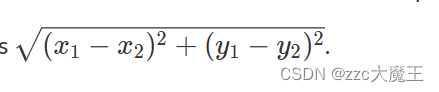

#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define all(x) x.begin(),x.end()
#define EX exit(0)
#define fr first
#define se second
//#define endl '\n'
using namespace std;
using ll=long long;void solve(){int n;cin>>n;int x[n+1],y[n+1];per(i,1,n){cin>>x[i]>>y[i];}per(i,1,n){int ansidx;bool flag=true;double dis;per(j,1,n){if(j!=i){if(flag){flag=false;ansidx=j;}else{double res=sqrt(pow(x[i]-x[j],2)+pow(y[i]-y[j],2));if(res>sqrt(pow(x[i]-x[ansidx],2)+pow(y[i]-y[ansidx],2))){ansidx=j;}}}}cout<<ansidx<<endl;}
}signed main(){ios::sync_with_stdio(false),cin.tie(nullptr);int t=1;while(t--)solve();return 0;
}

C - Colorful Beans

输入 N 种豆子，每种豆子美味度Ai，颜色Ci。

问：每个颜色的最小值x1,x2,x3,x4。max{x1,x2,x3,x4}是多少

#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define all(x) x.begin(),x.end()
#define EX exit(0)
#define fr first
#define se second
//#define endl '\n'
using namespace std;
using ll=long long;void solve(){int n;cin>>n;int ans=0;map<int,int>f;int a[n+1],c[n+1];per(i,1,n){cin>>a[i]>>c[i];if(!f[c[i]])f[c[i]]=a[i];else if(a[i]<f[c[i]])f[c[i]]=a[i];//同颜色里面取最小值}for(auto [color,val]:f){ans=max(ans,val);}cout<<ans;
}signed main(){ios::sync_with_stdio(false),cin.tie(nullptr);int t=1;while(t--)solve();return 0;
}

D - Medicines on Grid

从S点出发，是否能走到T点，每走一步花费 1 点能量，如果能量为 0 则不能走。（刚开始能量为0）

样例前面的 4*4 给的是网格图。

后面的 4 行是网格上的能量点：1,1,3就是点{1,1}上有能量 3。

当你在能量点上面的时候，你可以将目前有的能量变成当前能量点的数量。（注意不是增多也不是减少，是变成那个值）并且只能使用一次。

如果说暴力搜索我们考虑一种情况。

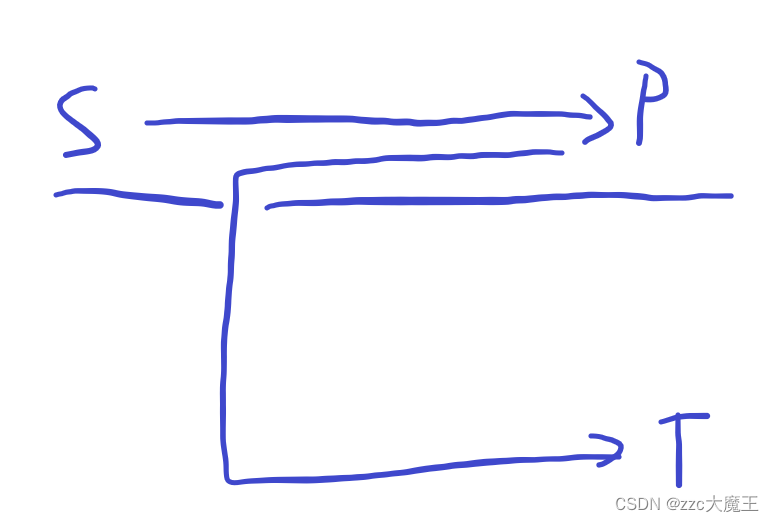
P是图上的能量点，必须要拿到这个能量点，才能到达终点T。

所以暴力搜索不行，如果历史点只访问一次，不会超时，但是答案错了。

如果每个点都走，那时间复杂度肯定爆了。

通过上面的分析可以发现，终点一定来自于能量点。

这样我们可以去找，能量点之间是否可以相互到达，以及能量点是否可以到达终点。

如果某个能量点可以被走到，并且这个能量点可以到达终点。那么就有解。

然后就是惊天大模拟：

起点是能量点的话，进队列，然后遍历剩下没被走过的能量点，看是否能被走到，能就加入队列，顺便判断一下是否能到终点即可。

BFS一次的复杂度是H*W=4e4（BFS求能量点到其他点的最短路）

而且题目中能量点最多只有300个

从每个能量点出发BFS一次，一共3e2*4e4≈1e7（刚好通过题目）

代码仅供参考，~~本蒟蒻写的太多了，可读性很差~~

#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define all(x) x.begin(),x.end()
#define EX exit(0)
#define fr first
#define se second
//#define endl '\n'
using namespace std;
using ll=long long;void solve(){int h,w;cin>>h>>w;string s[h+1];per(i,1,h){cin>>s[i];s[i]="0"+s[i];}struct Node{int x,y,val;}S,T;per(i,1,h){per(j,1,w){if(s[i][j]=='S'){S={i,j,0};}if(s[i][j]=='T'){T={i,j,0};}}}int n;cin>>n;//. 代表格子为空//# 代表障碍//S 起点//T 目标点//消耗 1 点能量水平或者垂直移动到相邻的空的格子//能量为0不能移动//(Ri,Ci)上有药，可以将能量设置成Ei，只能使用一次//BFS一次复杂度4e4   //最多300个补给点int r[n+1],c[n+1],e[n+1],toT[n+1],toS[n+1];map<array<int,2>,int>f;map<pair<int,int>,int>g;map<int,pair<int,int>>p;per(i,1,n){cin>>r[i]>>c[i]>>e[i];f[{r[i],c[i]}]=e[i];g[{r[i],c[i]}]=i;//补给点标号}int dis[305][305];//补给点到补给点的距离per(i,1,300){per(j,1,300){dis[i][j]=INT_MAX>>1;}}per(i,1,n)toS[i]=toT[i]=INT_MAX>>1;per(i,1,n){//toS,补给点去S的距离，toS去T的距离Node now={r[i],c[i],0};queue<Node>q;q.push(now);bool vis[h+1][w+1];per(i,1,h){per(j,1,w){vis[i][j]=false;}}int dx[4]={0,0,1,-1};int dy[4]={1,-1,0,0};while(q.size()){//BFSNode now=q.front();q.pop();if(vis[now.x][now.y])continue;if(f[{now.x,now.y}]){dis[i][g[{now.x,now.y}]]=min(dis[i][g[{now.x,now.y}]],now.val);dis[g[{now.x,now.y}]][i]=min(dis[g[{now.x,now.y}]][i],now.val);}if(now.x==S.x and now.y==S.y){toS[i]=min(toS[i],now.val);}if(now.x==T.x and now.y==T.y){toT[i]=min(toT[i],now.val);}vis[now.x][now.y]=true;per(i,0,3){Node nxt={now.x+dx[i],now.y+dy[i],now.val+1};if(nxt.x>=1 and nxt.x<=h and nxt.y>=1 and nxt.y<=w){if(s[nxt.x][nxt.y]!='#'){q.push(nxt);}}}}}if(!f[{S.x,S.y}]){//起始点没有能量cout<<"No";}else{//从补给点S开始能到达哪些点queue<int>q;bool vis[n+1];per(i,1,n)vis[i]=false;per(i,1,n){if(r[i]==S.x and c[i]==S.y){//起点,能量为e[i]q.push(i);vis[i]=true;}}while(q.size()){int now=q.front();q.pop();per(i,1,n){if(!vis[i]){if(e[now]>=dis[now][i]){vis[i]=true;q.push(i);}}}}per(i,1,n){if(vis[i] and e[i]>=toT[i]){cout<<"Yes";return;}}cout<<"No";}
}signed main(){ios::sync_with_stdio(false),cin.tie(nullptr);int t=1;while(t--)solve();return 0;
}