二叉树的介绍-编程知识

二叉树的介绍

学习堆排序时先了解下二叉树，因为堆排序中使用了二叉树。

一、二叉树介绍

二叉树（binary tree）树的每个节点最多有2个孩子节点。注意，这里是最多有2个，也可能只有1个，或者没有孩子节点。

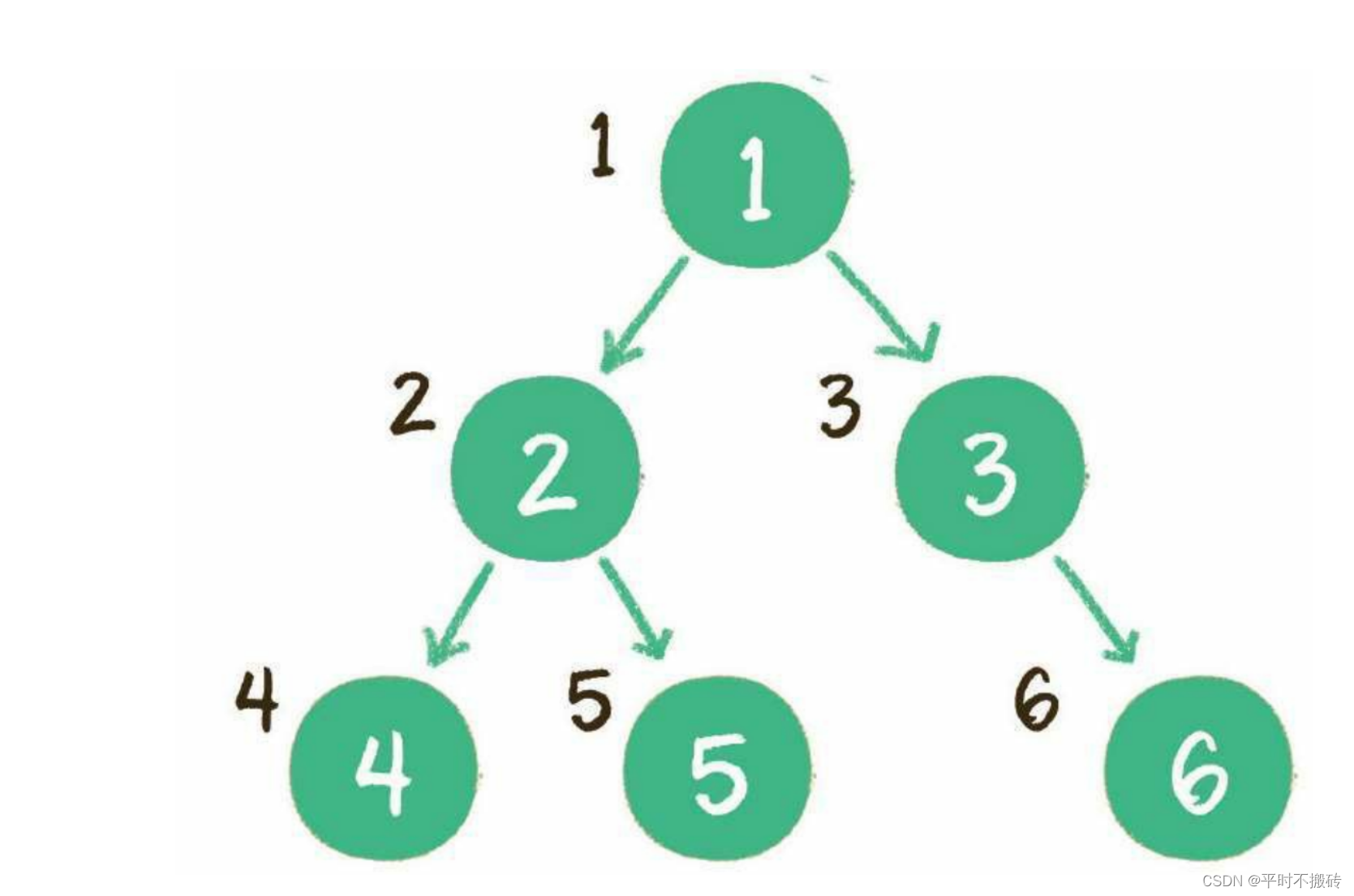
二叉树结构如图
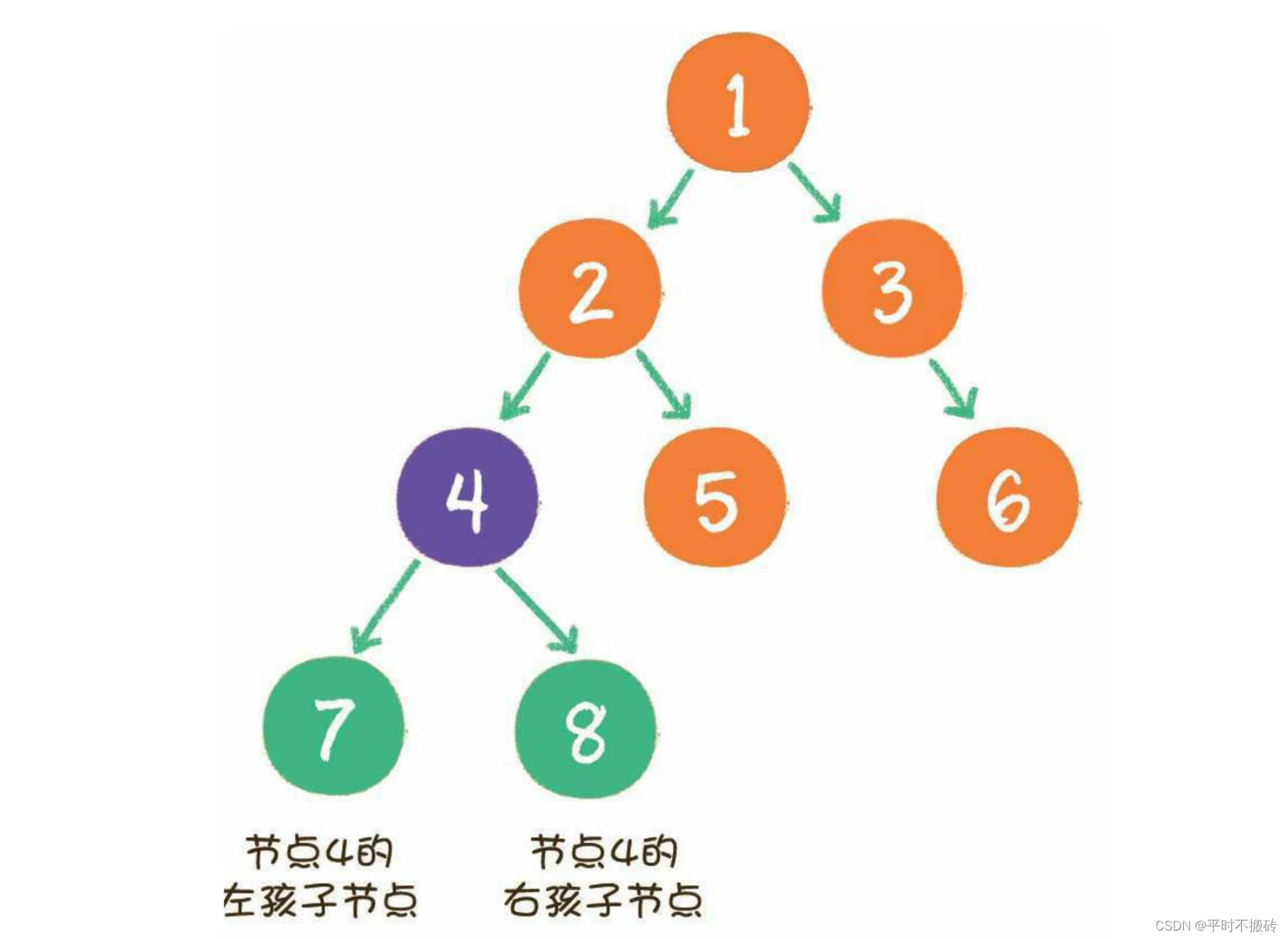
在这里插入图片描述

二叉树还有两种特殊的结构

满二叉树：二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上，那么这个树就是满二叉树。
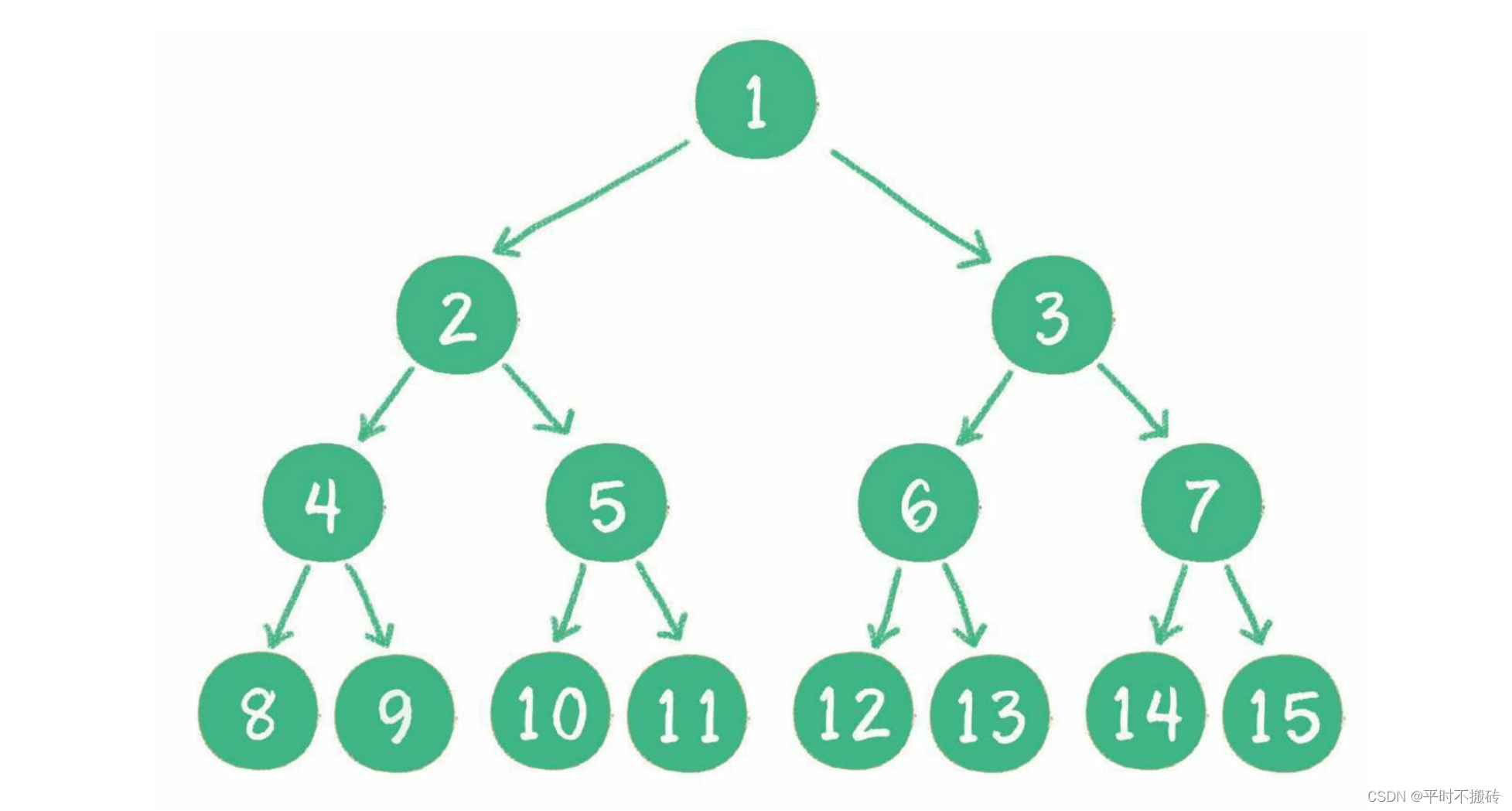
完全二叉树：完全二叉树的条件没有满二叉树那么苛刻，满二叉树要求所有分支都是满的；而完全二叉树只需保证最后一个节点之前的节点都齐全即可。

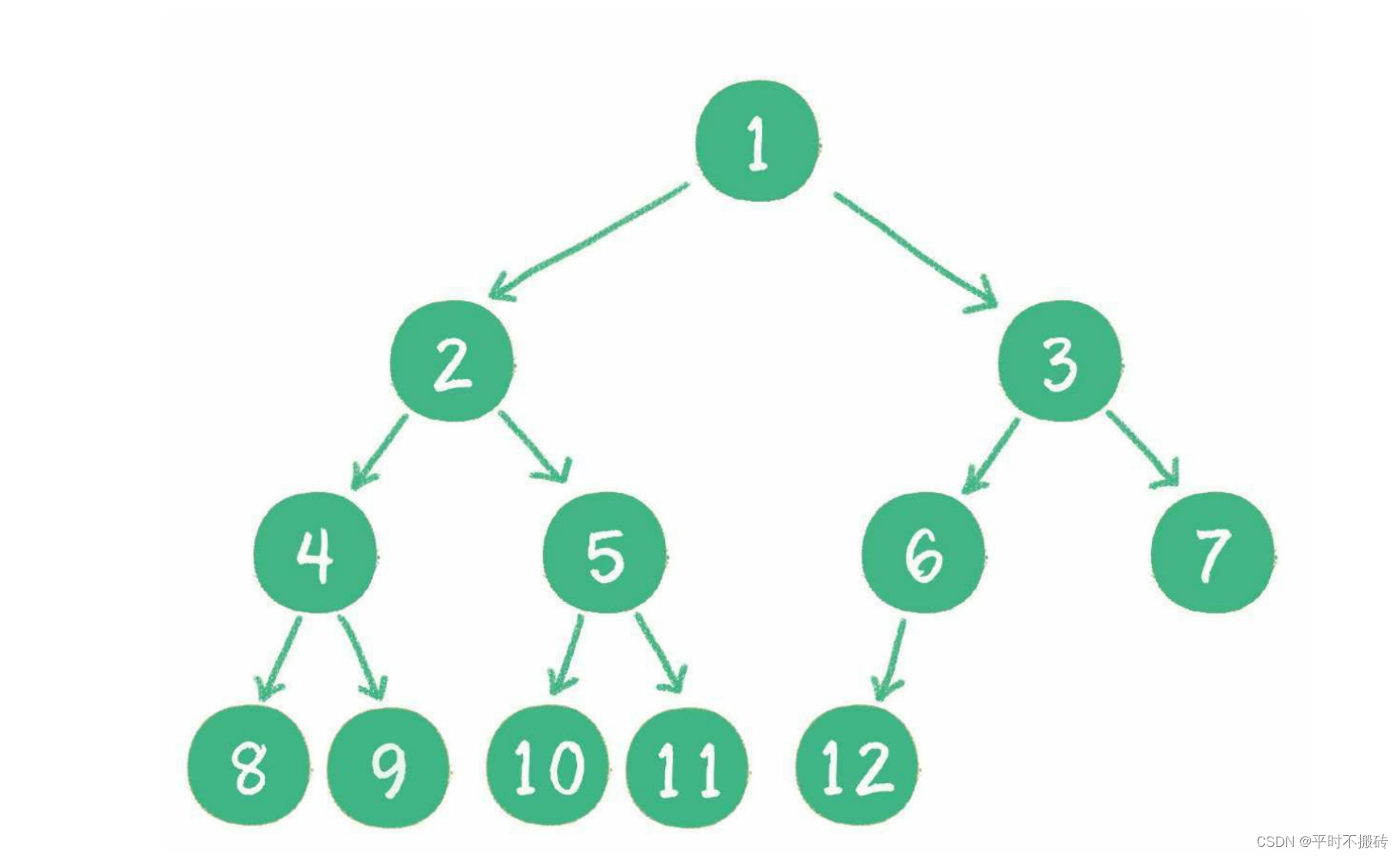
二、二叉树的数据结构

二叉树既可以用链表表示也能使用数组来表示。以下是使用Python实现这两种表示方式的示例。

链表表示

在链表表示中，每个节点通常包含三个字段：数据字段，左子节点引用和右子节点引用。我们可以定义一个简单的Node类来表示二叉树的节点，并使用这个类来构建二叉树。
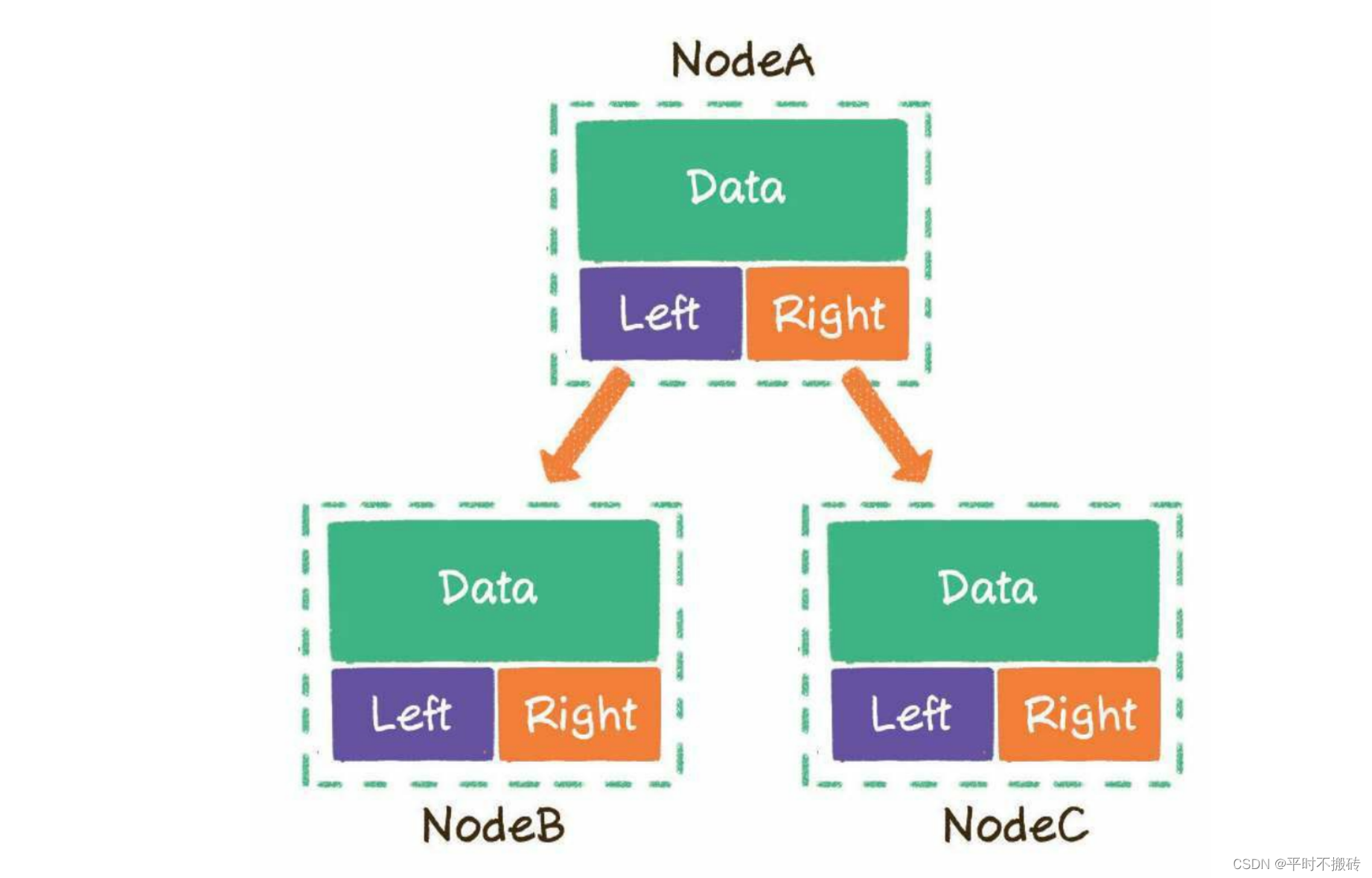
在这里插入图片描述

class Node:  def __init__(self, data):  self.data = data  self.left = None  self.right = None  # 示例：创建一个简单的二叉树  
root = Node(1)  
root.left = Node(2)  
root.right = Node(3)  
root.left.left = Node(4)  
root.left.right = Node(5)

数组表示

在数组表示中，对于索引为i的节点，其左子节点的索引为2i+1，右子节点的索引为2i+2（基于0的索引）。
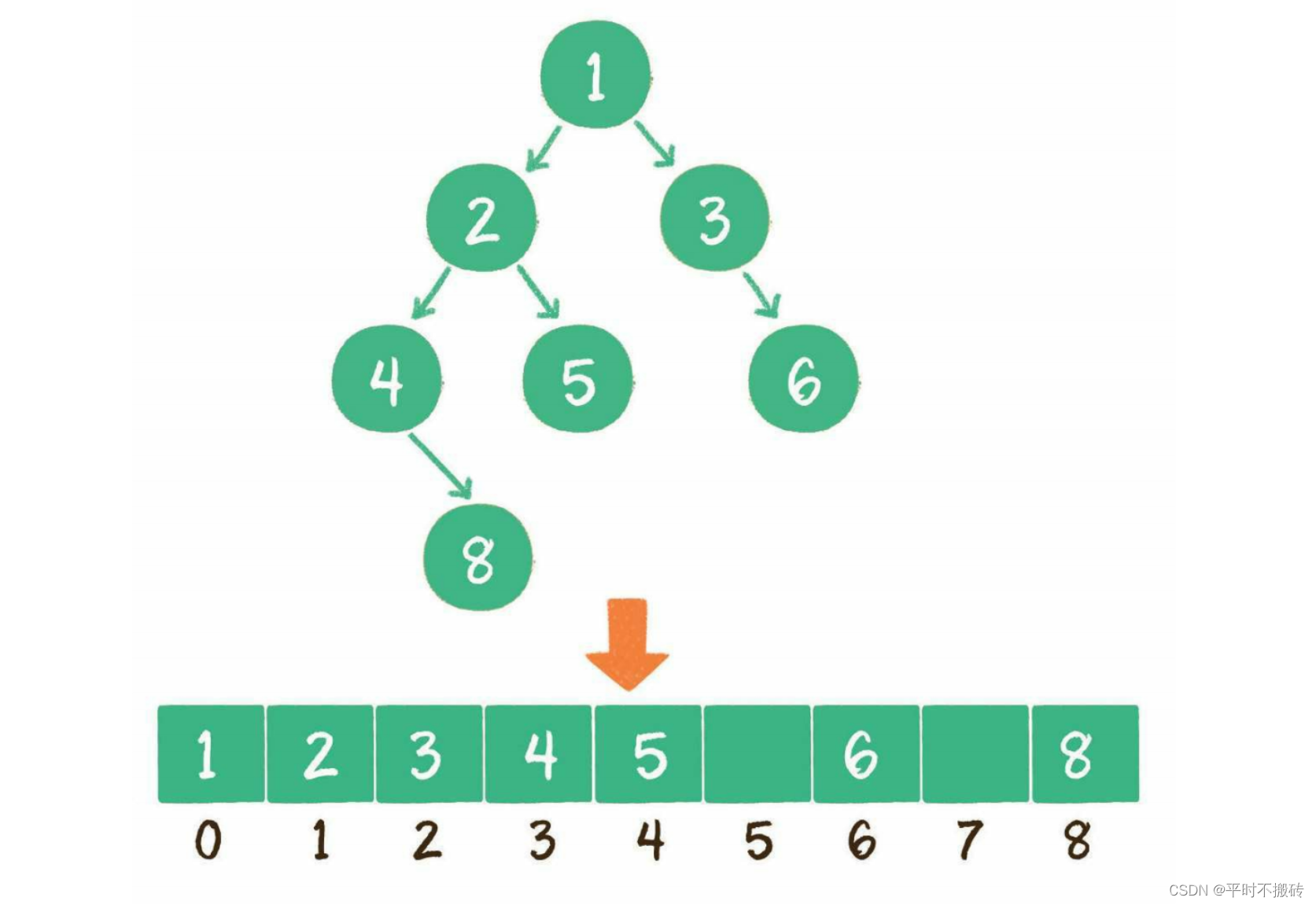
在这里插入图片描述

# 示例：
binary_tree_array = [1, 2, 3, 4, 5, None, 6, None, 8]  # None代表空节点  # 获取左子节点和右子节点的函数  
def get_left_child(parent_index, array):  return array[2 * parent_index + 1] if 2 * parent_index + 1 < len(array) else None  def get_right_child(parent_index, array):  return array[2 * parent_index + 2] if 2 * parent_index + 2 < len(array) else None  # 示例：访问根节点的左右子节点  
left_child = get_left_child(0, binary_tree_array)  
right_child = get_right_child(0, binary_tree_array)  
print(f"Left child of root: {left_child}")  
print(f"Right child of root: {right_child}")

在实际应用中，链表表示更加灵活，因为用链表表示更加直观，且当树不是完全二叉树时，会浪费存储空间。在Python中，由于链表节点的动态分配和引用关系的灵活性，链表表示更为常见。

三、二叉树的遍历

因为树并不是一个线性结构，所以树的遍历并没有列表那么简单，二叉树的遍历分为以下四种：

前序遍历
中序遍历
后序遍历
层序遍历

前序遍历

遍历规则是：先根节点，再左节点，最后再是右节点。
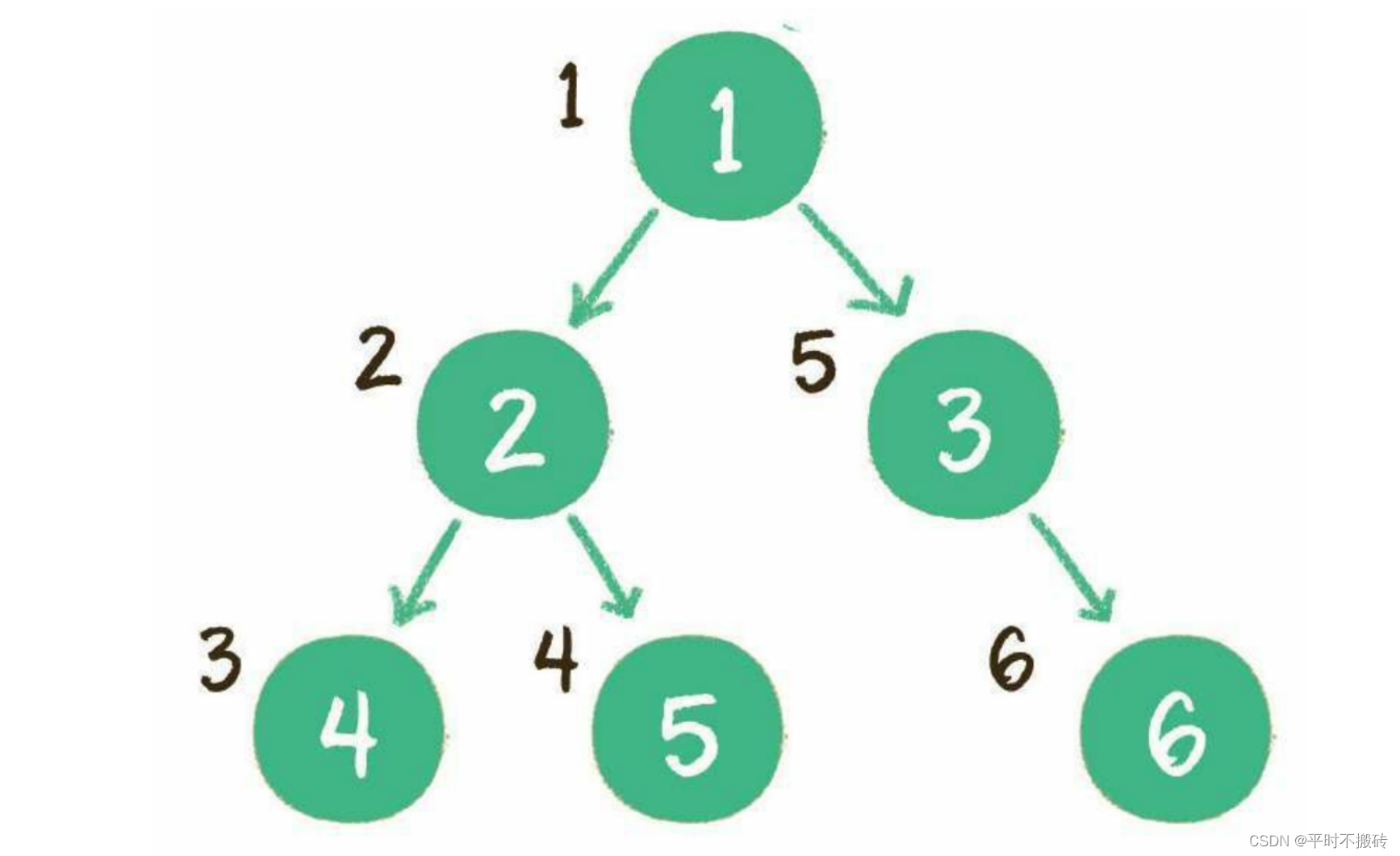
在这里插入图片描述

class Node:def __init__(self, data):self.data = dataself.left = Noneself.right = Nonedef preorder_traversal(root):if root is None:return []result = [root.data]result += preorder_traversal(root.left)result += preorder_traversal(root.right)return result# 示例
node1 = Node(1)
node2 = Node(2)
node3 = Node(3)
node4 = Node(4)
node5 = Node(5)
node6 = Node(6)
node1.left = node2
node1.right = node3
node2.left = node4
node2.right = node5
node3.right = node6
print("前序遍历:", preorder_traversal(node1))

中序遍历

遍历规则: 先左子树、再根节点、最后右子树。
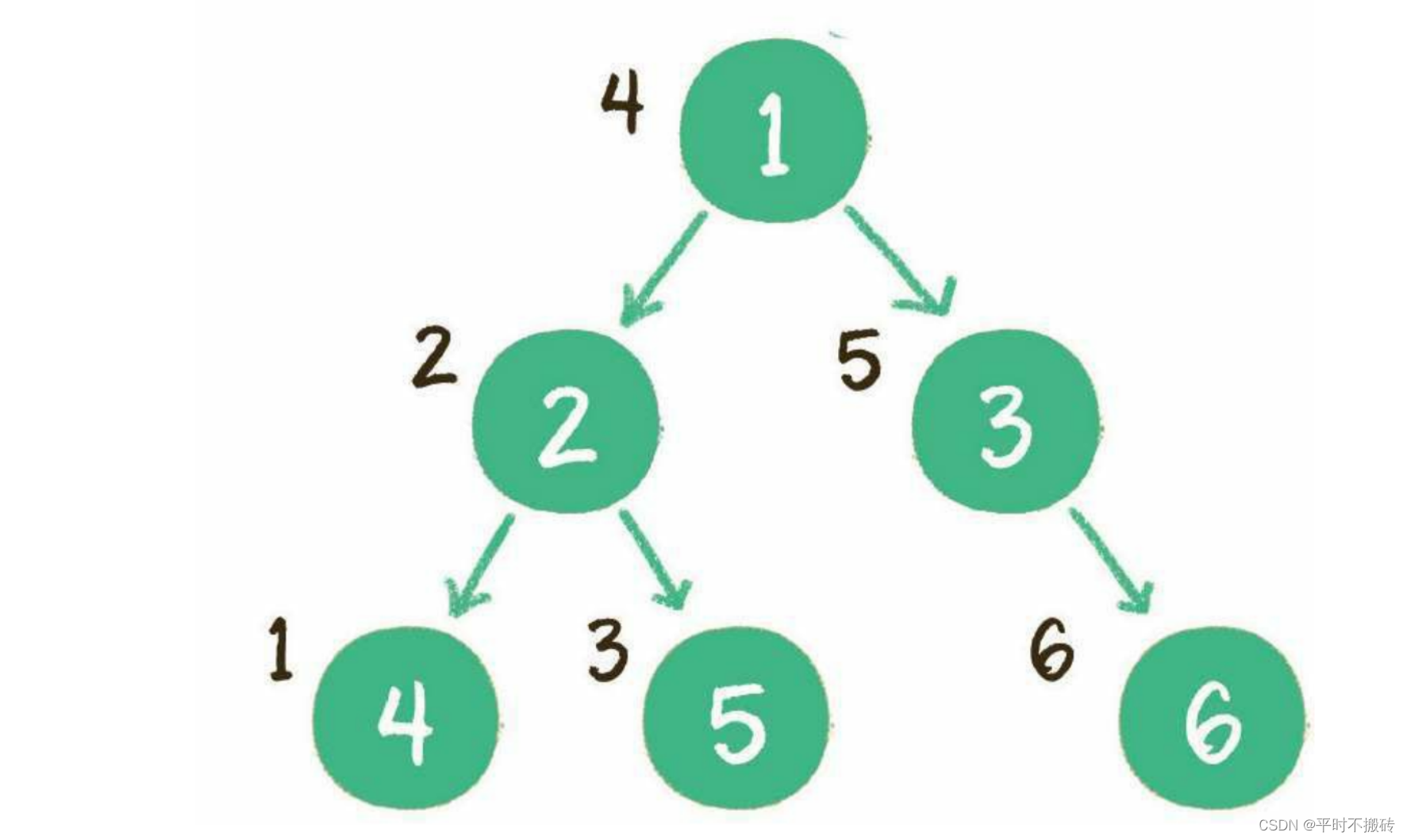
在这里插入图片描述

class Node:def __init__(self, data):self.data = dataself.left = Noneself.right = Nonedef inorder_traversal(root):if root is None:return []result = inorder_traversal(root.left)result += [root.data]result += inorder_traversal(root.right)return result# 示例
node1 = Node(1)
node2 = Node(2)
node3 = Node(3)
node4 = Node(4)
node5 = Node(5)
node6 = Node(6)
node1.left = node2
node1.right = node3
node2.left = node4
node2.right = node5
node3.right = node6
print("中序遍历:", inorder_traversal(node1))

后序遍历

遍历规则：先左子树、再右子树、最后根节点。
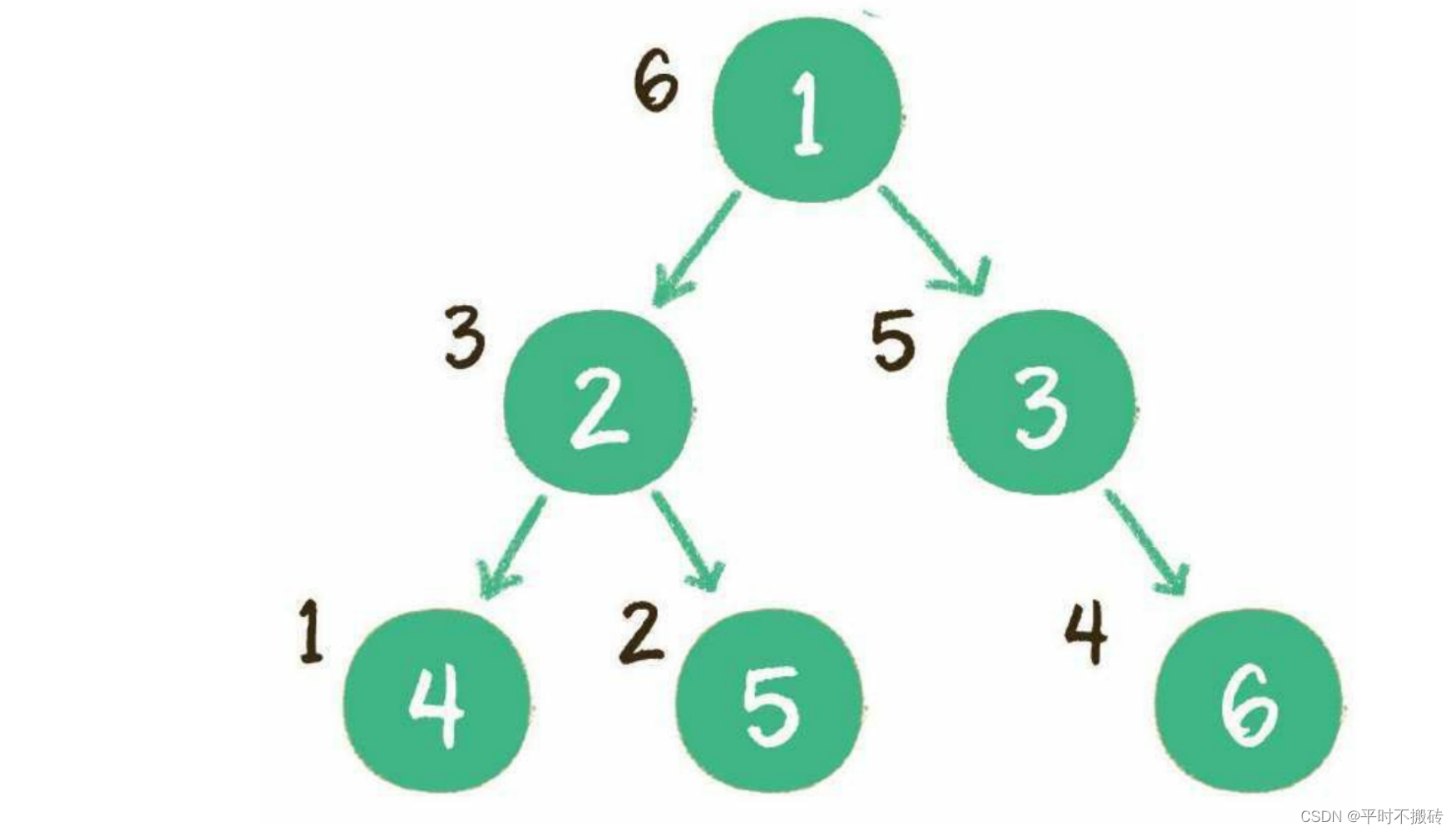
在这里插入图片描述

class Node:def __init__(self, data):self.data = dataself.left = Noneself.right = Nonedef postorder_traversal(root):if root is None:return []result = postorder_traversal(root.left)result += postorder_traversal(root.right)result += [root.data]return result# 示例
node1 = Node(1)
node2 = Node(2)
node3 = Node(3)
node4 = Node(4)
node5 = Node(5)
node6 = Node(6)
node1.left = node2
node1.right = node3
node2.left = node4
node2.right = node5
node3.right = node6
print("后序遍历:", postorder_traversal(node1))

层序遍历

遍历规则：照从根节点到叶子节点的层次关系，一层一层横向遍历各个节点，从上至下，从左至右。
在这里插入图片描述

from collections import dequeclass Node:def __init__(self, data):self.data = dataself.left = Noneself.right = Nonedef levelorder_traversal(root):if root is None:return []result = []queue = deque([root])while queue:level_size = len(queue)level_nodes = []for _ in range(level_size):node = queue.popleft()level_nodes.append(node.data)if node.left:queue.append(node.left)if node.right:queue.append(node.right)result.append(level_nodes)return result# 示例
node1 = Node(1)
node2 = Node(2)
node3 = Node(3)
node4 = Node(4)
node5 = Node(5)
node6 = Node(6)
node1.left = node2
node1.right = node3
node2.left = node4
node2.right = node5
node3.right = node6
print("层序遍历:", levelorder_traversal(node1))