1. 引言

前序博客：

• 递归证明——cycles of curves是必选项？

‘Foreign field’ 或 ‘non-native field’ 算术在ZKP（zero knowledge proof零知识证明）系统中随处可见。若想使用 ZKP 进行：

• 布尔运算
• 公钥密码学
• 或 证明组合

则无疑会遇到由于foreign field运算而导致的约束爆炸。
然而，若查看Arkworks等开源代码库（如https://github.com/arkworks-rs/r1cs-std/blob/master/src/fields/emulated_fp/mod.rs），会发现：

• 开发人员处理此问题的通用方式已经有一段时间没有更新了。

人们经常说，“可使用composition组合在受限 L1 (ETH) 上获得 XYZ 证明系统”，但：

• 如果不创建新颖且通常极具创造性的方法来处理“non-native”域运算，这是不切实际的。
• 事实上，协议经常会在 Gas 费方面遭受巨大打击，因为它们无法找出更优化的证明组合。

那么什么是foreign域以及处理它们的最新技术是什么？

foreign域运算是指：

• 对，属于与ZKP系统的native有限域不同的有限域元素进行运算。

有限域基础知识可参看：

• Wiki Finite field

如，ZKP 系统可能会使用一个大的素数域 (Fp) 进行本机操作，但需要证明有关另一个素数域 (Fq) 中的元素的陈述。之所以会出现挑战，是因为：

• 就所需约束的数量而言，用 Fp 表示 Fq 中的foreign域元素非常昂贵。

foreign域运算的低效率是：

• ZKP系统的实际可扩展性和成本的主要瓶颈，特别是对于本质上需要在多个域中操作的应用程序，如证明组合。
• 证明组合涉及验证证明，而该证明本身验证其他证明，需要在不同域进行“嵌套”操作。
  • 如，将Nova或Lasso等证明系统放入 Groth16 Wrapper中进行链上验证。
  • 或者在另一个可能具有更好内存效率的证明方案（如Nova）中使用Lasso证明。

2. 再次尝试 Lasso/JOLT

可通过在 Grumpkin 曲线上运行 Lasso 并使用 Groth16 进行组合来尝试证明组合。这意味着将整个 Lasso Verifier变成 BN254 scalar域上的电路。 Lasso 有几个涉及验证的步骤，其中之一是：

• 多项式承诺方案 (PCS)。当前的代码库使用 Hyrax PCS。
  • Hyrax Verifier在 Grumpkin base域（等于 BN254 scalar域）上执行两次 MSM。

在电路中使用的Grumpkin椭圆曲线中，scalar域为 Fr，而曲线的base域为 Fq。电路通常对应scalar域。Multi-scalar multiplication (MSM) 涉及计算椭圆曲线点的线性组合，其中scalar是 Fr 元素，point是Projective元素（坐标为 Fq域/也称为曲线的基域）。使用 Arkworks，可在电路中使用 NonNativeFieldVar 完成这项工作，这有一些优化…但仍然会导致数百万个约束。开销大约是 500 倍！

然后，电路将做sum-check Verifier工作，该工作具有潜在的non-native运算（Lasso/Jolt 中的sum-check Verifier将在 Grumpkin scalar域上工作，即 BN254 base域）。这样，将再次导致约束爆炸：

• Testudo, https://github.com/cryptonetlab/testudo是一个常见的代码库，人们可以参考它来了解其工作原理。该项目在 PCS 完成之前就停止了，但他们确实在电路中做了sum-check。

3. 那该怎么办？

许多人建议改用具有logarithmic对数Verifier开销的 PCS，如：

• HyperKZG：https://github.com/microsoft/Nova/blob/main/src/provider/hyperkzg.rs
• 或Zeromorph：Zeromorph: Zero-Knowledge Multilinear-Evaluation Proofs from Homomorphic Univariate Commitments

这确实有助于让Verifier进入一种“gas”费用更少的状态。在某些情况下，L1 甚至会为特定 PCS 准备好预编译。然而，如上所示，这种side-stepping侧步仍然不是最佳的，因为Verifier电路的其他部分将继续使用non-native域工作。即使研究人员不遗余力地消除它们，如：

• 在CycleFold: Folding-scheme-based recursive arguments over a cycle of elliptic curves中，尝试让Verifier “on-chain上链”时仍然存在成本。这意味着最终，将需要以某种方式或形式面对non-native域工作！

最先进的文献进展为：

• 2024年论文Beyond the circuit: How to Minimize Foreign Arithmetic in ZKP Circuits。在该论文中，作者介绍了三个涉及foreign域工作的新概念：
  • 1）使用拒绝采样，来证明，不同groups（即具有不同素数阶）的离散对数相等，的协议。这避免了在证明statment中嵌入foreign group运算。
  • 2）一种 Σ 协议，允许在电路外部执行椭圆曲线标量乘法，并使用哈希函数将其绑定到电路。这避免了电路内部昂贵的non-native域运算。像 Poseidon 这样的哈希函数在电路中工作非常高效。
  • 3）一种使用单个lookup argument来证明 AES 加密知识的算法，避免了电路中所需的布尔运算的。

其中：

• Σ 协议是一种令人惊讶的直接方式，将艰苦的工作委托给证明者，并让电路简单地使用哈希。
  

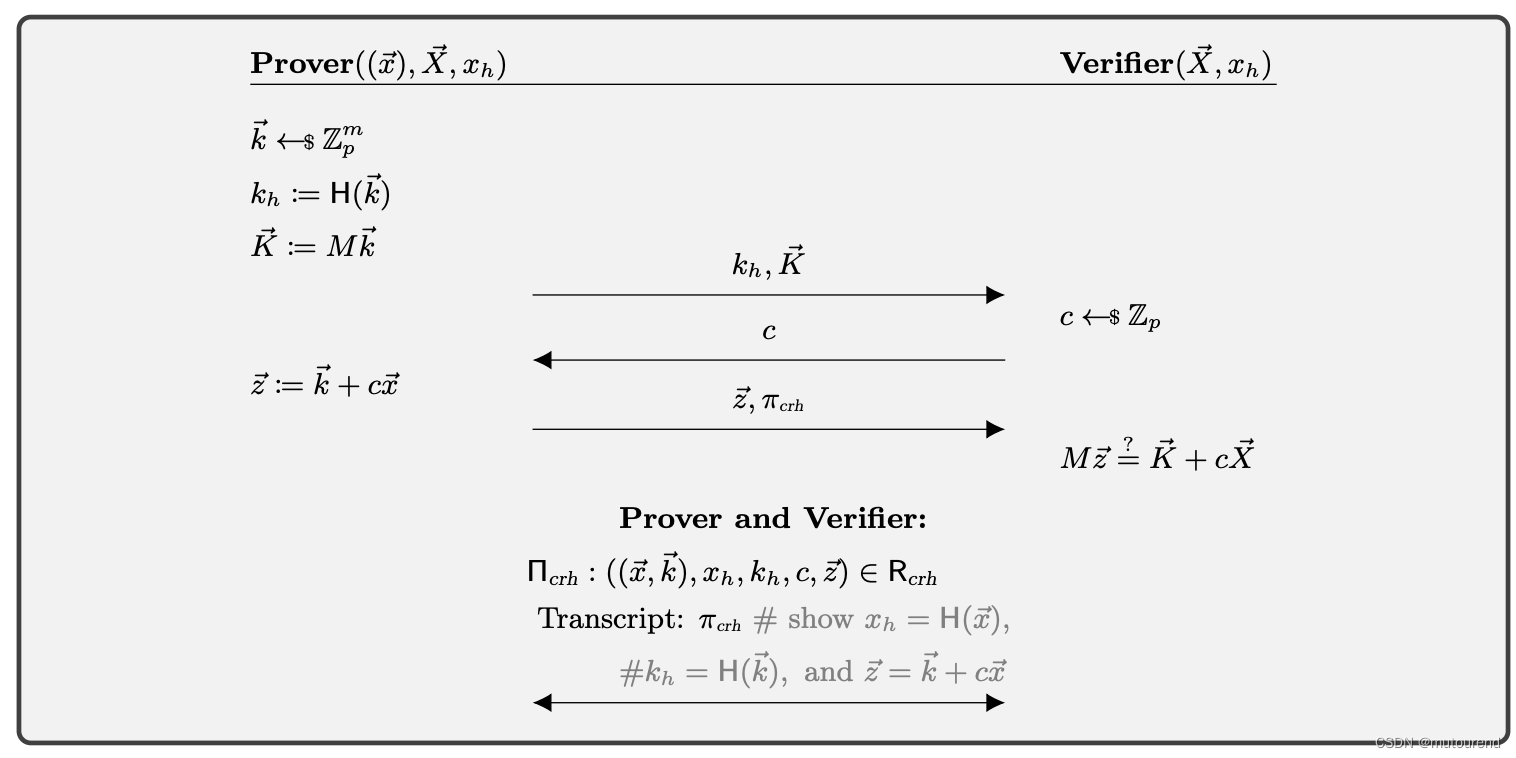
在这种情况下，电路中避免了non-native工作，但Verifier仍然需要进行检查。如果这些是曲线点，这不太可能成为问题，但在更一般的情况下，如矩阵向量乘积或 MSM 之类的东西，受约束的 L1 Verifier可能太昂贵而无法在实践中使用。

4. 有没有办法从电路中去除foreign域，同时保持较低的Verifier成本？

若可将 SigmaKit 的技巧与其他技术结合使用，就可创建电路和Verifier开销都很低的通用技术 (SigmaSuite)。这将成为在证明组合中处理foreign域运算的最先进技术。

有几个可能的方向可以实现这一点。如：

• 多次执行 Σ 协议技术，将工作移出电路并允许更简单的Verifier。第二步出现了问题，因为现在正在电路中对大vectors向量进行哈希处理。也许可通过默克尔树或哈希链来处理这些？然后，这个问题再次成为Verifier潜在的巨大成本。

Testudo 工作表明，对 R1CS 中的 Groth16 进行sum-check实际上是可能的。ICME团队建议：

• 使用 SigmaKit 的 Σ 协议结合sum-check协议来从电路中删除non-native域运算。
  • in-circuit sum-check Verifier可用于检查相等性并创建最终的压缩证明（Groth16）；否则，这些检查将由Verifier合约完成。
  • 此外，如果使用 Groth16，可以使用SnarkPack或其他方法聚合证明。这些技术的结合将产生用于证明组合的高性能电路（无需non-native域工作），并仍为链上Verifier提供简洁的证明。

ICME团队期待为这些工具的开源套件做出贡献，用于各种non-native域运算任务。 Sigmabus (SigmaSuite) 的想法可以添加到 Arkworks 或 Bellperson 等项目中并供所有人使用。

ICME团队致力于：

• 为NovaNet构建“The modular ZKP layer” 。

参考资料

[1] ICME 2024年4月4日博客 The cost of composition: an exploration in the state of the art for foreign field arithmetic in zero knowledge proofs