在二叉搜索树中，旋转操作是维护树平衡的重要技术之一，特别是在红黑树这种自平衡树结构中。旋转操作可以通过改变树中节点之间的父子关系来优化树的结构，从而保持树的平衡，确保树的操作效率。
在本文中，我们将详细介绍LEFT-ROTATE操作，这是一种在红黑树中常用的旋转技术。

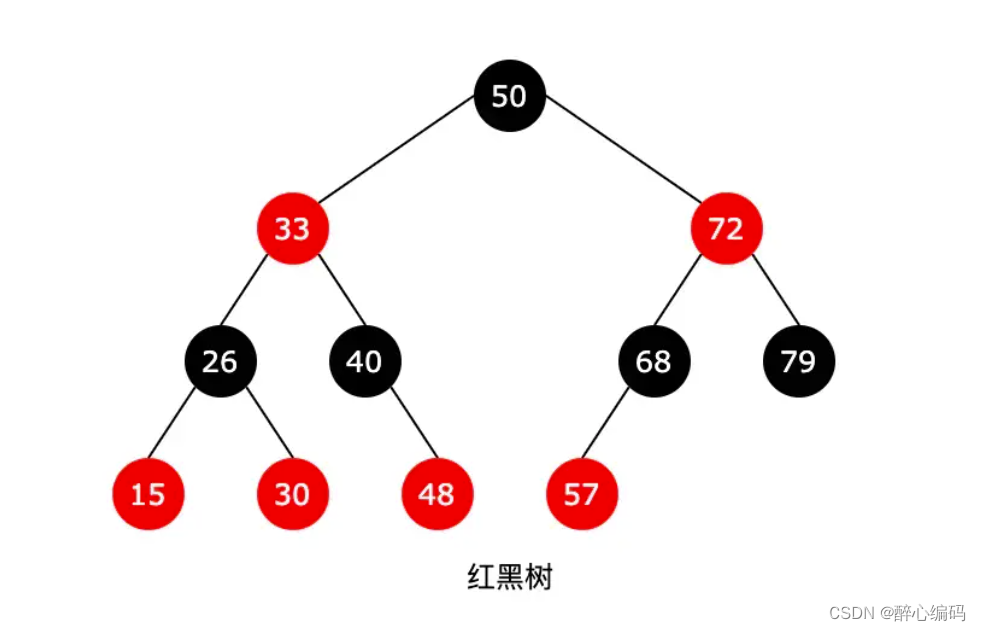
一、什么是LEFT-ROTATE？

LEFT-ROTATE是一种在二叉搜索树上进行的局部调整操作，它的目的是将某个节点的右孩子提升为新的父节点，同时将原父节点降为新根节点的左孩子。这种操作通常在插入或删除节点后进行，以修复可能违反红黑树性质的情况。

二、LEFT-ROTATE的步骤

LEFT-ROTATE操作可以分为以下几个步骤：

1. 选择旋转节点：首先，我们需要确定旋转的中心节点x。这个节点x是我们要提升其右孩子的节点。

2. 确定新根节点：x的右孩子y将成为新根节点。在旋转过程中，y将取代x在其父节点中的位置。

3. 调整子节点关系：将y的左孩子（如果有的话）赋值给x的右孩子。这样，原来的y的左孩子现在变成了x的右孩子。

4. 更新父节点指针：更新x的父节点指针，使其指向y。这是因为x现在成为了y的左孩子。

5. 调整颜色（在红黑树中）：如果在红黑树中进行旋转，还需要考虑颜色的调整。这通常涉及到检查和重新着色x和y，以保持红黑树的性质。

6. 更新父节点指针（在红黑树中）：如果在红黑树中，还需要更新x和y的父节点指针，以反映新的树结构。

三、LEFT-ROTATE的效果

通过LEFT-ROTATE操作，我们可以有效地调整树的结构，使得树更加平衡。这种操作有助于保持红黑树的性质，特别是确保从根节点到每个叶子节点的所有路径上黑色节点的数量相同。

四、例子

假设我们有以下的二叉搜索树：

    x/ \y   T.nil

其中x是旋转节点，y是x的右孩子。执行LEFT-ROTATE操作后，树的结构变为：

  y/ \
x  T.nil

在这个例子中，y成为了新的根节点，而x成为了y的左孩子。

五、伪代码示例

以下是LEFT-ROTATE操作的伪代码，假设我们有一个红黑树T，需要对节点x进行左旋操作：

FUNCTION LEFT-ROTATE(T, x)y = x.right  // y is the right child of xT.nil = y.left // T.nil is a sentinel node representing the nil leavesIF T.nil != y THENy.left = x  // The former right child of x becomes the new parent of its old left childENDIFx.right = y.left  // x's new right child is the former left child of yy.left = x  // y becomes the left child of x// Update the parent pointers and colors if necessary (for red-black trees)// Update the parent pointer of xx.p = y.p// If y was the child of the root, update the root of the treeIF y.p == NIL THENT.root = yELSE IF y == y.p.left THENy.p.left = yELSEy.p.right = yENDIF// Update the parent pointer of yy.p = x// Red-black tree specific adjustments (omitted for simplicity)
ENDFUNCTION

六、伪代码示例

以下是一个完整的C代码示例，实现了红黑树的左旋操作。请注意，这个示例仅包括左旋操作的函数，并没有包含整个红黑树的实现，例如插入、删除和平衡调整等其他相关函数。

#include <stdio.h>
#include <stdlib.h>// 定义颜色常量
#define RED   0
#define BLACK 1// 红黑树节点结构
typedef struct rb_node {int key;int color;struct rb_node *left;struct rb_node *right;struct rb_node *parent;
} rb_node;// 红黑树结构
typedef struct {rb_node *root;
} rb_tree;// 创建新的红黑树节点
rb_node* create_node(int key) {rb_node* new_node = (rb_node*)malloc(sizeof(rb_node));if (!new_node) return NULL;new_node->key = key;new_node->color = RED; // 新节点总是红色的new_node->left = NULL;new_node->right = NULL;new_node->parent = NULL;return new_node;
}// 左旋函数实现
void left_rotate(rb_tree *T, rb_node *x) {rb_node *y = x->right;// 确保x有一个右孩子if (!y) return;// 设置y的左孩子为x的右孩子x->right = y->left;if (y->left) {y->left->parent = x;}// 将y提升为x的父节点的位置y->parent = x->parent;if (x->parent) {if (x == x->parent->left) {x->parent->left = y;} else {x->parent->right = y;}} else {T->root = y; // x是树的根节点，旋转后y成为根节点}// 设置x为y的左孩子y->left = x;x->parent = y;// 这里我们没有处理颜色变化，因为在完整的红黑树实现中，// 颜色变化通常与插入和删除操作一起处理，以维护红黑树的性质。
}// 主函数，用于测试左旋操作
int main() {// 创建红黑树和一些节点rb_tree T;T.root = create_node(5); // 根节点T.root->left = create_node(3); // 左孩子T.root->left->left = create_node(1); // 左孩子的左孩子T.root->left->right = create_node(4); // 左孩子的右孩子T.root->right = create_node(7); // 右孩子T.root->right->left = create_node(6); // 右孩子的左孩子// 执行左旋操作left_rotate(&T, T.root->left); // 围绕节点3进行左旋// 打印旋转后的树结构（这里需要一个中序遍历函数）// ...return 0;
}

在这个示例中，我们首先定义了红黑树节点和树的结构，然后实现了创建新节点和左旋操作的函数。在main函数中，我们创建了一个简单的红黑树，并执行了一次左旋操作。

请注意，这个代码示例没有处理红黑树的颜色变化，这通常在插入和删除操作中一并处理。此外，为了完整地实现红黑树，还需要实现其他辅助函数，例如插入、删除、平衡调整等。

请注意，上述代码仅为示例，实际的红黑树实现会更复杂，包括颜色的维护和其他红黑树性质的保持。在实际应用中，还需要考虑哨兵节点（NIL）的处理，以及在插入和删除操作后进行的一系列平衡调整。

七、结论

LEFT-ROTATE是红黑树中的一种基本操作，它通过调整节点之间的关系来维护树的平衡。这种操作对于保持红黑树的高效性能至关重要，因为它确保了树的高度始终保持在O(log n)的范围内，从而保证了搜索、插入和删除等操作的效率。通过理解和掌握LEFT-ROTATE操作，我们可以更好地管理和优化红黑树，提高数据处理的性能。