方式一:string存储状态
题目传送门:845. 八数码 - AcWing题库
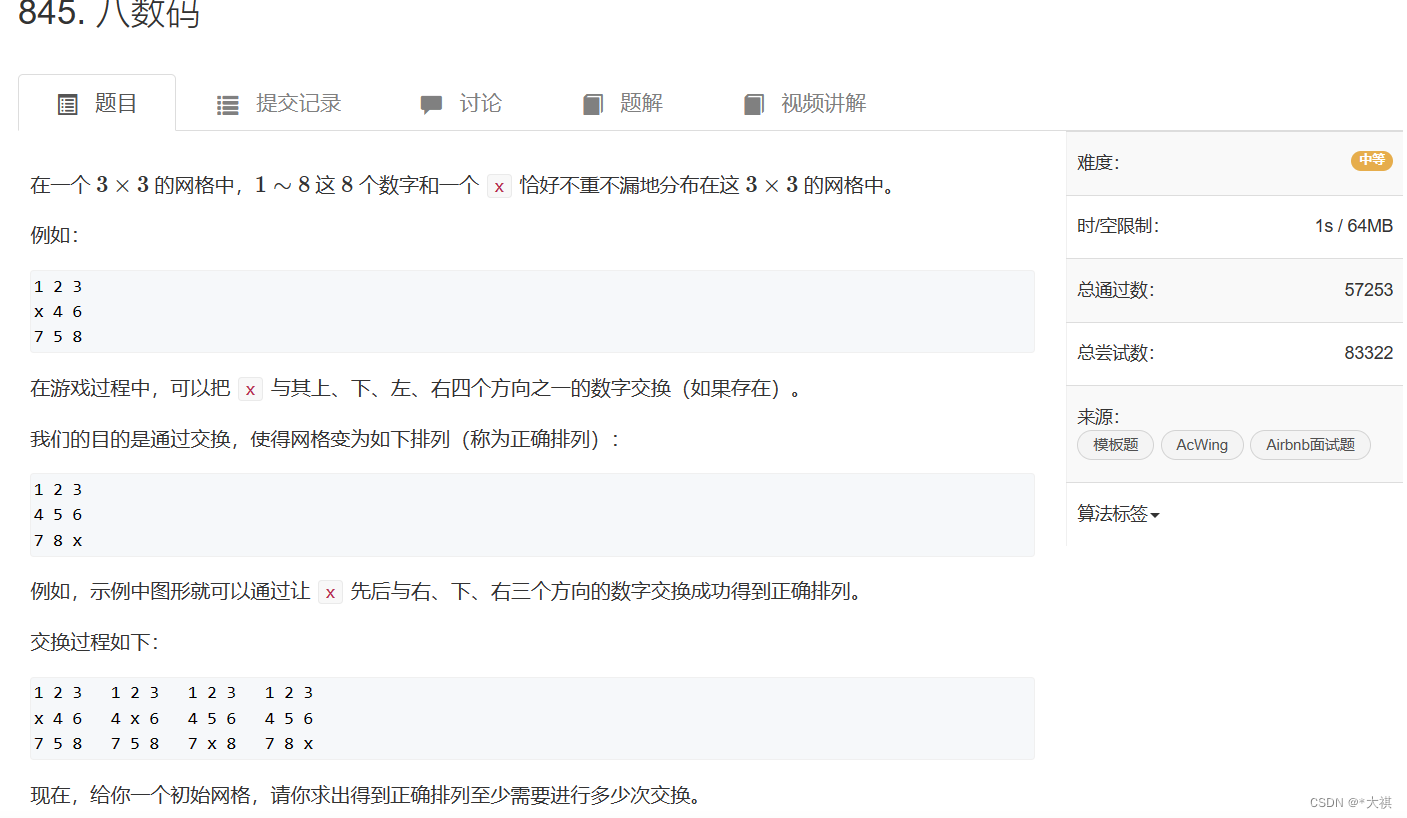
BFS适用于边权为1的最短路问题 ,而这题要求最少的交换次数,将每一次的九宫格状态当作一个“状态结点”,由当前这个结点可以扩展出其它状态【即 x 可以与其上下左右(若存在的话)交换】,每一种可能的交换都将是bfs“踏出的下一步结点”。
这题难在如何存储状态,并且同一种状态将会有多种方式得出,需要 “ 去重 ” 保存状态,每一个状态对应到达该状态的最短路(即x的交换次数)是多少,于是我们想到用map来存【状态-步数】,同样bfs队列里也加入到达的状态,九宫格的状态可以用字符串来表示。
编码阶段:九宫格转换为字符串存储
解码阶段:字符串转换为九宫格后 ,再加以交换操作
编码和解码的转换通过stirng的下标 与 九宫格的横纵坐标的联系来实现:设字符 x 在string中的下标为t,则在九宫格a中为 a[t/3][t%3] 。(下标都从0开始)同样地,九宫格中某个数字的横纵坐标分别为x和y,则其在sting中存储的下标应为 x*3+y。
本题还学到了swap交换的对象之广泛,可以直接对string中的两个字符做交换。
(此外unordered_map在此题中比普通map要快)
上代码:
#include<iostream>
#include<queue>
#include<string>
#include<unordered_map>
using namespace std;
int dx[]={-1,0,1,0},dy[]={0,1,0,-1}; //下标偏移数组,分别对应x的上右下左
unordered_map<string,int> mp;
queue<string> q;
int bfs(){string s;while(!q.empty()){s=q.front();q.pop();int stp=mp[s];if(s=="12345678x")return stp;int t=s.find('x'); //寻找下标int x=t/3, y=t%3; //由下标得到横纵坐标for(int i=0,tx,ty;i<4;i++){tx=x+dx[i];ty=y+dy[i];if(tx<0||tx>=3||ty<0||ty>=3)continue;//注意此处是>=3不是>3int t2=tx*3+ty; //转换为横纵坐标swap(s[t],s[t2]);if(!mp.count(s)){ //判重mp[s]=stp+1;q.push(s);}swap(s[t],s[t2]);}}return -1;
}
int main(){ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);string s,t;for(int i=0;i<9;i++){cin>>t;s+=t;}q.push(s);mp[s]=0;cout<<bfs();return 0;
}
方式二:用一个数(long long)存储状态
当然,这个适合输入全是数的情况(如x换为0)
题目传送门:P1379 八数码难题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
犯过的错就是,注意横纵坐标对应,从0开始存的就横纵坐标<3,从1开始存的就<=3 QAQ
直接上代码:
#include<iostream>
#include<map>
#include<queue>
using namespace std;
typedef long long ll;
map<ll,int> mp;
queue<ll> q;
int dx[]={-1,0,1,0},dy[]={0,1,0,-1},a[5][5];
ll t;
int bfs(){while(!q.empty()){t=q.front();q.pop();int stp=mp[t], x, y;if(t==123804765)return stp;//数转矩阵 for(int i=3;i>0;i--){for(int j=3;j>0;j--){a[i][j]=t%10;t/=10;if(!a[i][j])x=i, y=j;}}for(int i=0,tx,ty;i<4;i++){tx=x+dx[i];ty=y+dy[i];if(tx<1||tx>3||ty<1||ty>3)continue;swap(a[x][y],a[tx][ty]);//矩阵转数t=0;for(int i=1;i<=3;i++){for(int j=1;j<=3;j++){t=t*10+a[i][j];}} if(!mp.count(t)){mp[t]=stp+1;q.push(t);}swap(a[x][y],a[tx][ty]);}}
}
int main(){ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);//可忽略,关同步流来提速的cin>>t;q.push(t);mp[t]=0;cout<<bfs();return 0;
}