随想录日记part37

$time：$ 2024.04.06

---

---

主要内容：今天开始要学习动态规划的相关知识了，今天的内容主要涉及四个方面：
完全背包；零钱兑换 II ；组合总和 Ⅳ 和单词拆分

• 完全背包
• 518. 零钱兑换 II
• 377. 组合总和 Ⅳ
• 139.单词拆分

---

---

动态规划五部曲：
【1】.确定dp数组以及下标的含义
【2】.确定递推公式
【3】.dp数组如何初始化
【4】.确定遍历顺序
【5】.举例推导dp数组

Topic1完全背包

题目：

小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。他需要带一些研究材料，但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等，它们各自占据不同的重量，并且具有不同的价值。小明的行李箱所能承担的总重量为 N，问小明应该如何抉择，才能携带最大价值的研究材料，每种研究材料可以选择无数次，并且可以重复选择。

输入描述:

第一行包含两个整数，N，V，分别表示研究材料的种类和行李空间
接下来包含 N 行，每行两个整数 wi 和 vi，代表第 i 种研究材料的重量和价值

输出描述:

输出一个整数，表示最大价值。

输入：
$$\begin{gathered} 45 \\ 12 \\ 24 \\ 34 \\ 45 \end{gathered}$$
输出： $10$

思路：

接下来进行动规五步曲：
1.确定dp数组以及下标的含义:
dp[i]：行李空间为i时dp[i]能存下的最大价值。
2.确定递推公式:
dp[j]=Math.max(dp[j],dp[j-weights[i]]+values[i])
3.dp数组如何初始化
dp[0] 一定为0
4.确定遍历顺序
5.举例推导dp数组

代码如下：

import java.util.*;
class Main{public static void main (String[] args) {/* code */Scanner sc=new Scanner(System.in);int n=sc.nextInt();int v=sc.nextInt();int[] weights=new int[n];int[] values=new int[n];for(int i=0;i<n;i++){weights[i]=sc.nextInt();values[i]=sc.nextInt();}int[] dp=new int[v+1];dp[0]=0;for(int i=0;i<n;i++){for(int j=weights[i];j<=v;j++){dp[j]=Math.max(dp[j],dp[j-weights[i]]+values[i]);}}System.out.println(dp[v]);}
}

时间复杂度：$O(n\ast v)$
空间复杂度：$O(n)$

---

---

Topic2零钱兑换

题目：

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带符号整数。

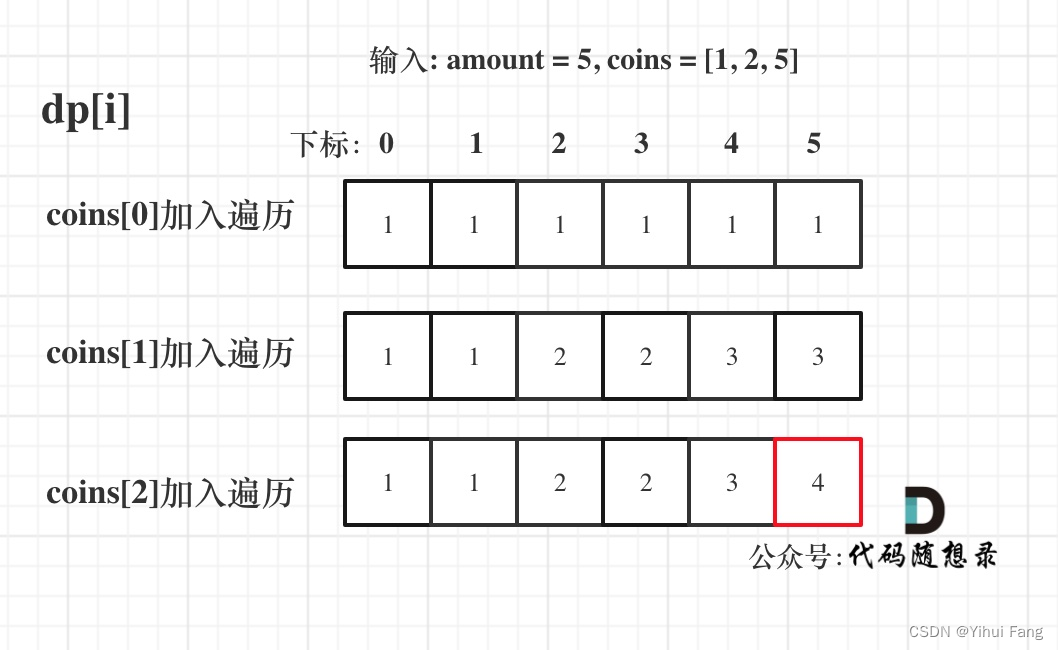
输入： $amount=5,coins=[1,2,5]$
输出： $4$
解释：
有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
思路：

按照上面的五个步骤进行分析：
1.确定dp数组以及下标的含义
dp[j]：凑足总额为j的方案数为dp[j]
2.确定递推公式
递推公式：dp[j] +=dp[j - coins[i]];
3.dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0，那么dp[0] = 0;
4.确定遍历顺序
5.举例推导dp数组

整体代码如下：

class Solution {public int change(int amount, int[] coins) {int[] dp=new int[amount+1];dp[0]=1;for(int i=0;i<coins.length;i++){for(int j=coins[i];j<=amount;j++){dp[j]+=dp[j-coins[i]];}}return dp[amount];}
}

时间复杂度：$O(n\ast amount)$
空间复杂度：$O(amount)$

---

---

Topic3组合总和

题目：

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。题目数据保证答案符合 32 位整数范围。

输入： $nums=[1,2,3],target=4$
输出： $7$
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。

思路：

按照上面的五个步骤进行分析：
1.确定dp数组以及下标的含义
dp[i]: 凑成目标正整数为i的排列个数为dp[i]
2.确定递推公式
dp[i] += dp[i - nums[j]]
3.dp数组如何初始化
dp[0]一定是1。
4.确定遍历顺序
如果求组合数就是外层for循环遍历物品，内层for遍历背包。
如果求排列数就是外层for遍历背包，内层for循环遍历物品。
5.举例推导dp数组

整体代码如下：

class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target + 1];dp[0] = 1;for (int i = 0; i <= target; i++) {for (int j = 0; j < nums.length; j++) {if (i >= nums[j])dp[i] += dp[i - nums[j]];}}return dp[target];}
}

时间复杂度：$O(target\ast n)$
空间复杂度：$O(n)$

---

---

Topic4单词拆分

题目：

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

输入： $s="leetcode",wordDict=["leet","code"]$
输出： $true$
解释：
返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。

思路：

按照上面的五个步骤进行分析：
1.确定dp数组以及下标的含义
dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词。
2.确定递推公式
如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，那么dp[i]一定是true。（j < i ）。所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
3.dp数组如何初始化
dp[0]一定是true。
4.确定遍历顺序
如果求组合数就是外层for循环遍历物品，内层for遍历背包。
如果求排列数就是外层for遍历背包，内层for循环遍历物品。
5.举例推导dp数组
整体代码如下：

class Solution {public boolean wordBreak(String s, List<String> wordDict) {HashSet<String> set = new HashSet<>(wordDict);boolean[] valid = new boolean[s.length() + 1];valid[0] = true;for(int i=1;i<=s.length();i++){for(int j=0;j<i&&!valid[i];j++){if(set.contains(s.substring(j,i))&&valid[j])valid[i]=true;}}return valid[s.length()];}
}

时间复杂度：$O(n^3)$
空间复杂度：$O(n)$

---

---

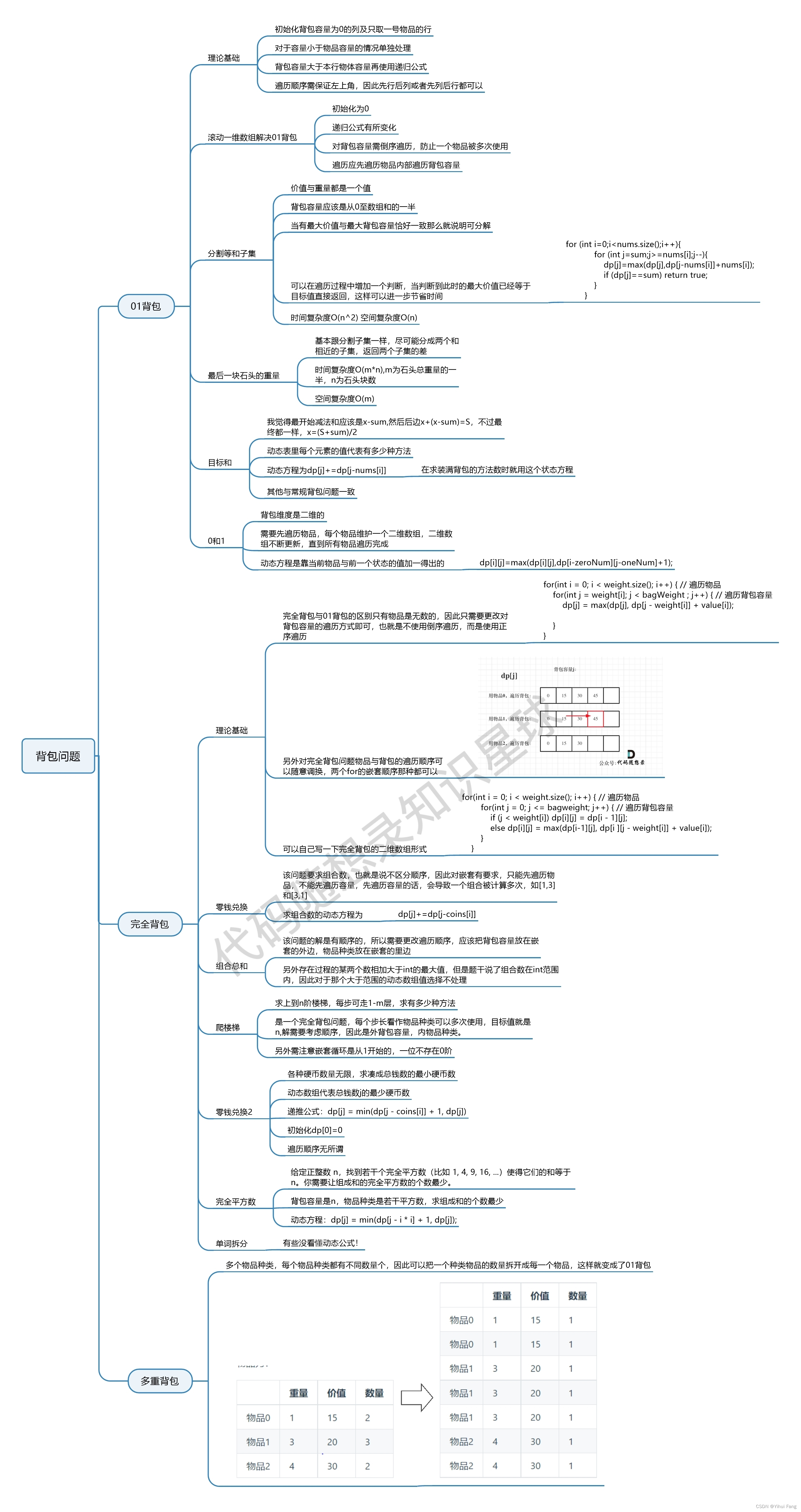
关于多重背包可以看这个链接
关于背包问题的总结看这个链接