原题链接:1388. 游戏 - AcWing题库
玩家一和玩家二共同玩一个小游戏。
给定一个包含 N 个正整数的序列。
由玩家一开始,双方交替行动。
每次行动可以在数列的两端之中任选一个数字将其取走,并给自己增加相应数字的分数。(双方的初始分都是 0 分)
当所有数字都被取完时,游戏结束。
分更高的一方获胜。
请计算,如果双方都采取最优策略进行游戏,则游戏结束时,双方的得分各是多少。
输入格式
第一行包含整数 N。
后面若干行包含 N 个整数,表示这个序列。注意每行不一定恰好包含一个数。
输出格式
共一行,两个整数,分别表示玩家一和玩家二的最终得分。
数据范围
2≤N≤100,
数列中的数字的取值范围为 [1,200]。
输入样例:
6
4 7 2 9
5 2
输出样例:
18 11
解题思路:
又是这种决策游戏,思想上还是有博弈论的,玩家一与玩家二都绝对的聪明都具有上帝视角,既让自己获得分数最大,也让对方获得的分数尽量少,两个玩家都是最优策略,不存在一方每次拿最大的,另一方每次拿最小的,而且应该每个玩家都有上帝视角。
样例:4,7,2,9,5,2
玩家一(先手):拿两边的4或2,但是我拿了4玩家二会拿7,我拿2,玩家二要么拿4要么拿5,这样7或9我势在必得一个,于是想了想我拿2
此时样例:4,7,2,9,5
玩家二:拿4的话玩家一会拿7,我拿5的话,玩家一会拿9,9>7,还是拿4划算
此时样例:7,2,9,5
玩家一:这时候肯定拿7,拿5的话,9就被玩家二拿去了
此时样例:2,9,5
玩家二:不管拿2,5都会让9被玩家1拿走,所有拿5,尽可能保证自己更大。
此时样例:2,9
玩家一:拿9
此时样例:2
玩家二:拿2,结束。
那么如何计算他们的分数呢,这就需要我们定义一个二维DP,可以看出样例中区间长度时不断递减的,每一次决策都会减少一个数,那么一个状态的DP可以由前一个状态转移过来,前一个要么取左边要么取右边,形成了此状态的DP,这不就是区间DP吗,dp[i][j]表示区间下表为i~j先手人获得的最大分数。
状态转移方程:dp[i][j]=max(w[i]+![\sum w[k] (i<k<=j)](https://latex.csdn.net/eq?%5Csum%20w%5Bk%5D%20%28i%3Ck%3C%3Dj%29) -dp[i+1][j], w[i]+
-dp[i+1][j], w[i]+ ](https://latex.csdn.net/eq?%5Csum%20w%5Bk%5D%28i%3C%3Dk%3Cj%29) -dp[i][j-1])
-dp[i][j-1])
这里定义的是dp[i][j]表示区间下表为i~j先手人获得的最大分数,假设选左边最优,既然选了那就要+w[i],为什么还要加上一个区间和(i<k<=j)还要减去dp[i+1][j],这里解释一下,既然选了左端点,那么区间就变为[i+1,j],玩家二的最优决策肯定时是dp[i+1][j],这个状态去转移玩家二下一次的最优决策,presum[j]-presum[i]为玩家二所能选的区间和,减去玩家二的最优决策所获得的分数,那么剩下的就是玩家一前一个状态的累计分数。
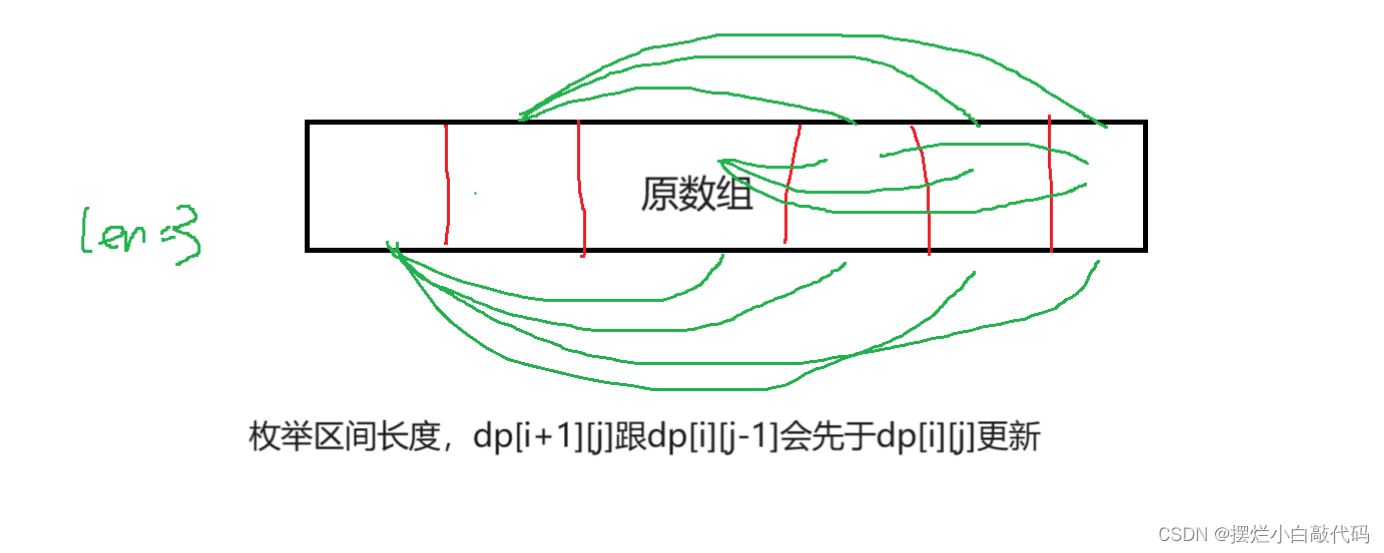
为了我们的状态能由上一个小状态转移过来,我们外循环枚举区间长度,这样保证了状态转移方程里面的数据已经更新了,内循环枚举区间起点,知道起点和区间长度,那么终点就可以计算出来。
AC代码:
#include<iostream>
using namespace std;
int n;
int w[105],dp[105][105],presum[105];//dp[i][j]为区间为i~j先手获得最大分数
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>w[i];presum[i]=presum[i-1]+w[i];}//区间DPfor(int len=1;len<=n;len++){//枚举区间长度for(int i=1;i+len-1<=n;i++){//枚举左端点int j=i+len-1;//右端点dp[i][j]=max(w[i]+presum[j]-presum[i]-dp[i+1][j],w[j]+presum[j-1]-presum[i-1]-dp[i][j-1]);//状态转移}}cout<<dp[1][n]<<" "<<presum[n]-dp[1][n]<<endl;return 0;
}题后总结:
这道题跟蓝桥杯练习系统的一个题很像,但好久没有写了,也忘记思路的,区间DP感觉很难理解,代码倒是很简洁。y总讲的是另一种定义,dp的含义是先手玩家与后手玩家分数的差值,虽然好理解一点,但是这种定义一般是想不出来的,这里就用了最一般的定义去写的,望大家理解。重难点在于状态转移方程,建议自己模拟一下过程,就很好理解了,文章说的比较多,若有错误的地方请大家指出,感谢观看。