文章目录
- 一、基础运算
- 二、矩阵的特殊运算
- 1、矩阵的转置
- 1.1、语法
- 1.2、示例
- 1.2.1、二维矩阵转置
- 1.2.2、更高维度的张量转置
- 2、方阵的行列式
- 2.1、计算行列式
- 2.2、示例:使用PyTorch计算行列式
- 3、方阵的迹
- 4、方阵的逆
- 4.1、计算矩阵的逆
- 4.2、使用PyTorch计算逆矩阵
二维张量又被称为矩阵。
对于矩阵的运算有加、减、逐元素乘、数乘、点积(矩阵乘法)、逐元素除、转置、逆、行列式。向量的点积(也称为内积或标量积)和矩阵的点积(通常指矩阵乘法)在数学上有不同的定义和用途,因此它们的计算方式也不相同。
一、基础运算
- 加法:矩阵的形状必须相同或者满足广播要求
- 减法:矩阵的形状必须相同或者满足广播要求
- 乘法(逐元素乘):矩阵的形状必须相同或者满足广播要求
- 除法:矩阵的形状必须相同或者满足广播要求
- 数乘
- 矩阵乘法:必须满足线性代数的矩阵乘法
import torch
matrix1=torch.tensor([[1,2,3],[1,2,3]])
matrix2=torch.tensor([[3,2,1],[3,2,1]])
matrix3=torch.tensor([[1,2],[1,2],[1,2]])
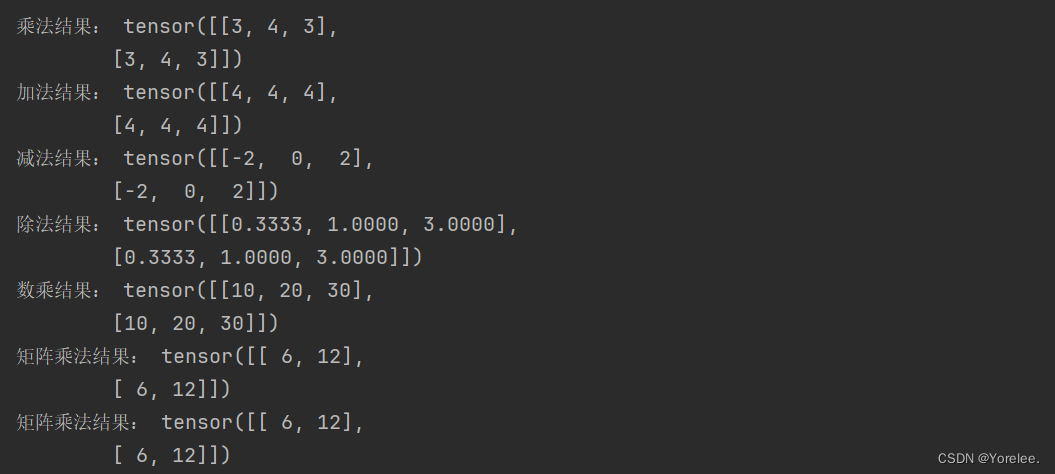
print("乘法结果:",matrix1*matrix2)
print("加法结果:",matrix1+matrix2)
print("减法结果:",matrix1-matrix2)
print("除法结果:",matrix1/matrix2)
print("数乘结果:",matrix1*10)
print("矩阵乘法结果:",matrix1@matrix3)#2×3 @ 3×2
print("矩阵乘法结果:",torch.matmul(matrix1,matrix3))#2×3 @ 3×2
二、矩阵的特殊运算
- 在PyTorch中,
torch.transpose函数是用来转置矩阵 - 在PyTorch中,可以使用
torch.det()函数计算方阵的行列式。 - 在PyTorch中,可以使用
torch.trace()函数计算方阵的迹。 - 在PyTorch中,可以使用
torch.inverse()函数计算方阵的逆。
1、矩阵的转置
在PyTorch中,torch.transpose 函数是用来转置矩阵或者更高维度的张量(Tensor)的。它可以交换张量的两个维度,对于二维张量(矩阵)来说,这等同于常规的矩阵转置操作。
torch.transpose对于二维张量(矩阵)来说,通常用于行列交换,等同于矩阵的转置操作。- 在处理多于两维的张量时,
torch.transpose提供了灵活性,可以选择任意两个维度进行交换。 - 如果需要对多维张量进行多次维度交换,可能会使用
torch.permute,它允许一次性重新排列多个维度。
1.1、语法
函数的基本语法如下:
torch.transpose(input, dim0, dim1)
input:要转置的输入张量。dim0:要交换的第一个维度。dim1:要交换的第二个维度。
1.2、示例
让我们看一些torch.transpose的使用示例:
1.2.1、二维矩阵转置
对于一个二维张量(矩阵),torch.transpose(matrix,0,1) 可以将其行和列交换。
import torch# 创建一个2x3的矩阵
x = torch.tensor([[1, 2, 3], [4, 5, 6]])
print("Original matrix:\n", x)# 转置矩阵
y = torch.transpose(x, 0, 1)
print("Transposed matrix:\n", y)
这将输出:
Original matrix:tensor([[1, 2, 3],[4, 5, 6]])
Transposed matrix:tensor([[1, 4],[2, 5],[3, 6]])
1.2.2、更高维度的张量转置
对于三维或更高维度的张量,torch.transpose可以用来交换任意两个维度。这很抽象,我们只需要关注矩阵的就行。
# 创建一个3x2x2的张量
x = torch.rand(3, 2, 2)
print("Original tensor shape:", x.shape)# 交换第一个维度和第二个维度
y = torch.transpose(x, 0, 1)
print("Transposed tensor shape:", y.shape)
这将输出形状变化的信息,例如,如果原始张量形状是(3, 2, 2),转置后的张量形状会是(2, 3, 2)。
2、方阵的行列式
行列式 det(A),是一个将 方阵 A 映射到实数的函数。矩阵的行列式是一个标量值,它提供了矩阵(线性变换)的一些重要性质的信息。对于一个方阵(即行数和列数相等的矩阵),其行列式可以通过多种方法计算,包括拉普拉斯展开、行列式的定义,或者更实用的方法,如LU分解。
行列式有几个重要的性质和几何意义:
- 非奇异性:一个矩阵是非奇异的(即可逆的)当且仅当其行列式不为零。
- 体积缩放因子:在几何上,一个方阵的行列式告诉我们,由该矩阵表示的线性变换改变了空间的多少倍体积。 如果行列式为1,意味着体积保持不变;如果行列式为负,意味着除了缩放,还进行了一个镜像反转。
- 行列式的乘积性:两个矩阵乘积的行列式等于这两个矩阵行列式的乘积,即det(AB) = det(A)· det(B)。
2.1、计算行列式
在PyTorch中,可以使用torch.det()函数计算方阵的行列式。
- .det: Expected a floating point or complex tensor as input.
2.2、示例:使用PyTorch计算行列式
import torch# 创建一个2x2的矩阵
A = torch.tensor([[1, 2], [3, 4]], dtype=torch.float)# 计算行列式
det_A = torch.det(A)
print(det_A)
输出:
tensor(-2.)
3、方阵的迹
方阵 A 的迹:对角线元素之和,通常表示为Tr(A)。
在PyTorch中,可以使用torch.trace()函数计算方阵的迹。
import torch# 创建一个2x2的矩阵
A = torch.tensor([[1, 2], [3, 4]])# 计算迹
Tr_A = torch.trace(A)
print(Tr_A)
输出:
tensor(5)
4、方阵的逆
矩阵的逆是线性代数中的一个重要概念,对于给定的方阵A,如果存在另一个方阵 B 使得 AB = BA = I,其中 I 是单位矩阵,则称 B 为 A 的逆矩阵。单位矩阵 I 是一个主对角线上所有元素都为1,其余元素都为0的方阵。
4.1、计算矩阵的逆
计算矩阵的逆可以通过多种方法实现,包括代数余子式法(对于小的矩阵)、高斯消元法或LU分解等。在计算机中,通常使用数值稳定的算法来计算较大矩阵的逆。
4.2、使用PyTorch计算逆矩阵
在PyTorch中,可以使用torch.inverse()函数计算方阵的逆。
import torch
A = torch.tensor([[1.0, 2.0], [3.0, 4.0]])
A_inv = torch.inverse(A)
print(A_inv)
这将输出矩阵 A 的逆:
tensor([[-2.0000, 1.0000],[ 1.5000, -0.5000]])


![[dvwa] CSRF](https://img-blog.csdnimg.cn/direct/79247570176e4b089d80d48f896262bf.png)