吴恩达机器学习理论基础
机器学习最常见的形式监督学习,无监督学习
线性回归模型概述
应用场景一:根据房屋大小预测房价
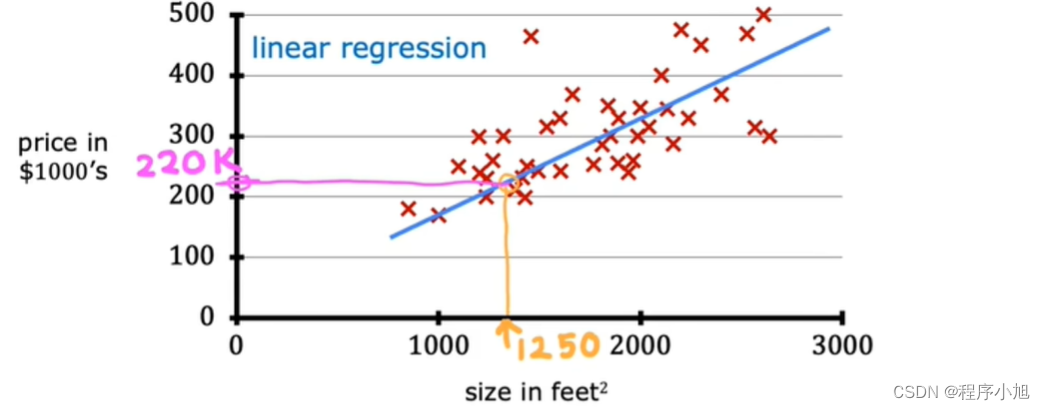
应用场景二:分类算法(猫狗分类)
核心概念:将训练模型的数据称为数据集(学习数据集以及描述数据集的基本符号)
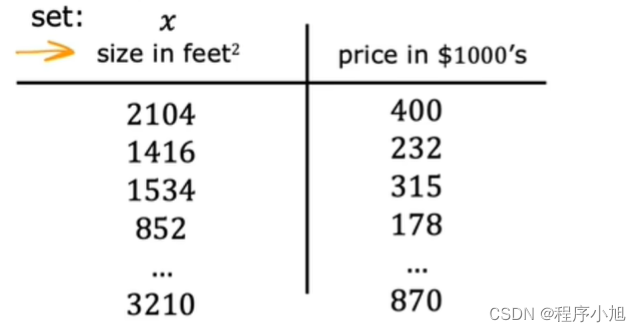
在机器学习中,这里表示输入的标准符号是小写的x,我们称之为输入变量,也称为特征或输入特征。
对于第一个训练示例(这对数字是(2104,400)。
监督学习中的训练集包括输入特征(例如房屋大小)和输出目标(例如房屋价格)。

其中函数f代表model(模型)是通常要学习的人工智能算法模型。将输入的特性通过模型进行预测给出输出的特征。
最简单的一种线性模型预测f(x)=wx+b的形式来进行回归预测分析(linear function)
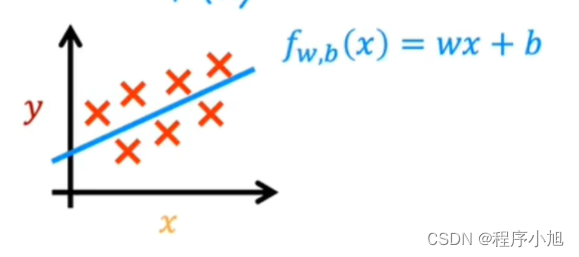
其中的函数f同样可能采用曲线的形式来进行描述,对于这种形式的模型我们统称为线性回归模型
更具体地说,这是具有一个变量的线性回归,其中短语“一个变量”表示只有一个输入变量或特征x,即房屋的大小。有一个输入变量的线性模型的另一个名称是单变量线性回归,其中 uni 在拉丁语中表示一个,而 variate 表示变量。
Cost Funcation代价函数(成本函数)
为了实现线性回归,第一个关键步骤是首先定义一个叫做成本函数的东西。
在机器学习中,模型的参数是您可以在训练期间调整以改进模型的变量。例如线性模型中的w和b两个参数(有时也称为系数或者权重)
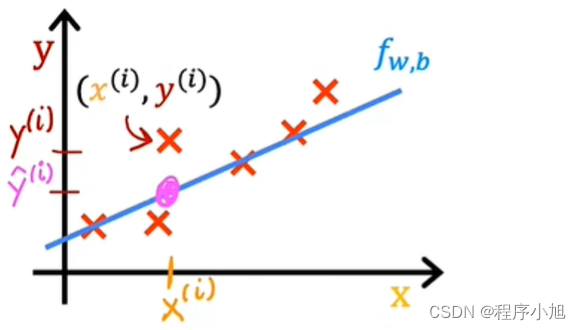
而成本函数(代价函数)是解决评价模型拟合程度的问题。通常常见的成本函数,包括了均方误差损失
线性回归中平方误差成本函数的数学表示
成本函数的实现实例分析
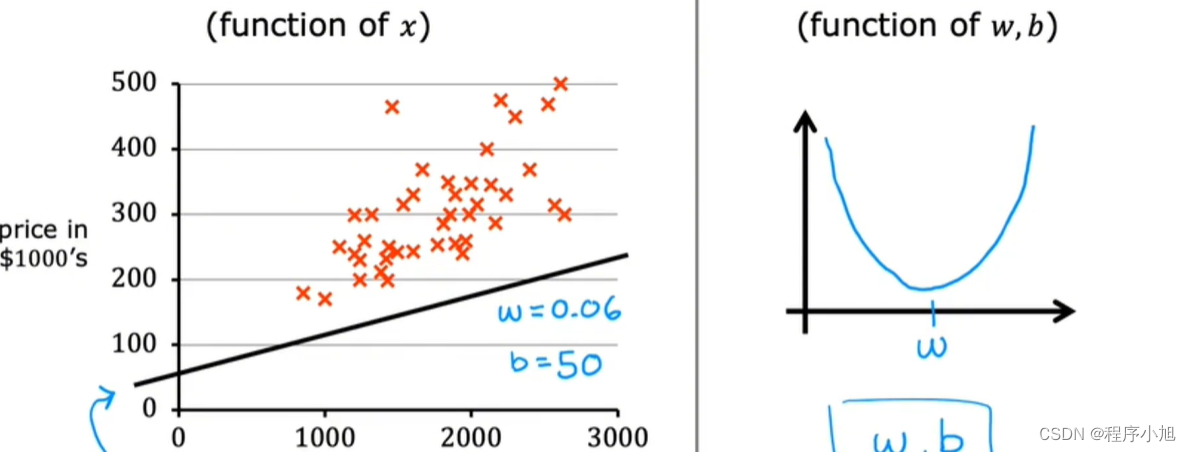
首先注意到,对于f下标w,当参数w固定不变,即始终为常数值时,则只是x的函数,也就是说y的估计值取决于输入x的值。
将b设置为0的情况

可以根据模型的预测结果来确定对应该线性模型的成本函数(损失函数)不同的参数w会对应不同的成本函数值如图当w=1时成本最小因此取1最为合适
成本函数由两个参数变为三个参数的变化示意图如下
加入参数b后变为三维空间中的一个曲面(函数)是一个3d曲面图形


此时整个曲面的最低点也就是成本函数取到最小值的地方,此处的参数w和参数b即是我们的线性回归模型所需要的参数信息。
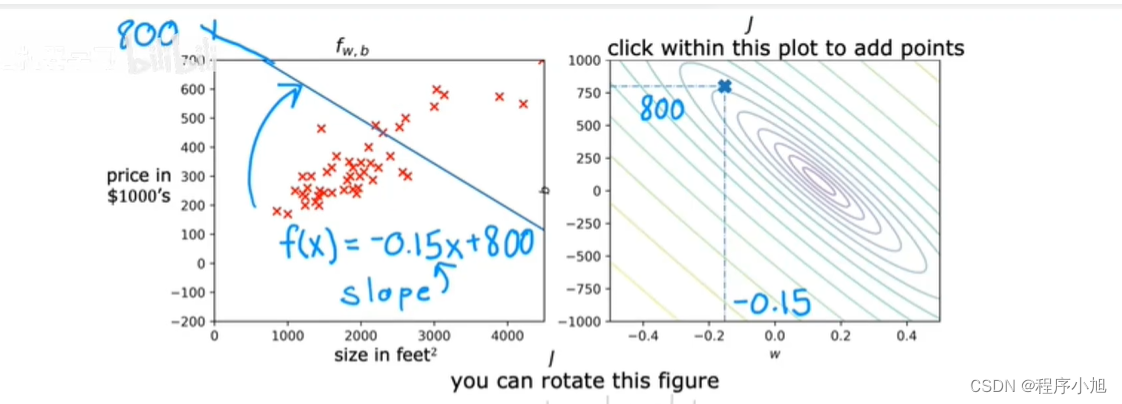
若此时沿z轴进行投影,可以得到等高线,沿梯度的方向进行移动可以确定最终的位置,为之后的梯度下降算法打下了一定的基础
线性回归线的对应关系线
成本函数取得最小值时所对应的情况
梯度下降(Gradient Descent)
你真正想要的是一种高效的算法,你可以用代码编写它来自动找到参数w和b的值,它们会给你最好的拟合线。使得成本函数取得最小值,可以通过梯度下降算法来进行实现
梯度下降和梯度下降的变体不仅用于训练线性回归,还用于训练所有 AI中一些最大和最复杂的模型。
梯度下降在机器学习中无处不在,不仅用于线性回归,还用于训练一些最先进的神经网络模型,也称为深度学习模型。
如图训练神经网络时所得到的成本函数(高度Z轴代表了成本函数值)

目标:从函数的顶部采用一定的算法,下降到函数的底部即成本函数对应最小的地方。