0 提纲

5.1 半监督学习
5.2 主动学习
5.3 代价敏感学习
5.4 多标签学习
5.5 多示例学习

1 半监督学习

用无标签的数据提升学习器的效果.

1.1 基本概念

半监督学习强调的是一种学习场景, 在该场景下, 无标签数据可以协助带标签数据提升预测质量.
监督学习: 训练数据都有标签, 相应的任务为分类、回归等.
无监督学习: 训练数据都没有标签, 相应的任务为聚类、特征提取 (如 PCA) 等.
半监督学习: 部分训练数据没有标签, 相应任务与监督学习一致.
从三者的关系可以看出, 半监督学习是从监督学习与无监督学习自然推导出来的.

1.2 学习场景

半监督学习的一大意义在于, 它导出了学习场景这个概念.

• 上午来了 100 个就诊者, 主治医生啥也没说, 实习生自悟, 把他们分成几个簇, 并且无法解释每簇的语义 (是否患病之类), 这是无监督学习场景中的聚类问题.
• 上午来了 100 个就诊者, 主治医生对每个人判断, 哪些患流感 (正例), 哪些没有 (负例). 实习生学习到流感的诊断方法. 下午来了新的就诊者, 实习生对他们进行诊断. 这是监督学习场景中的二分类问题.
• 上午来了 100 个就诊者, 主治医生对其中的 40 个人判断, 哪些患流感 (正例), 哪些没有 (负例). 实习生对剩下的 60 人进行诊断. 这是封闭世界半监督学习场景中的二分类问题.
• 上午来了 100 个就诊者, 主治医生对其中的 40 个人判断, 哪些患流感 (正例), 哪些没有 (负例). 下午来了新的就诊者, 实习生对他们进行诊断. 这是开放世界半监督学习场景中的二分类问题.

1.3 无标签数据协助提升学习器质量的讨论

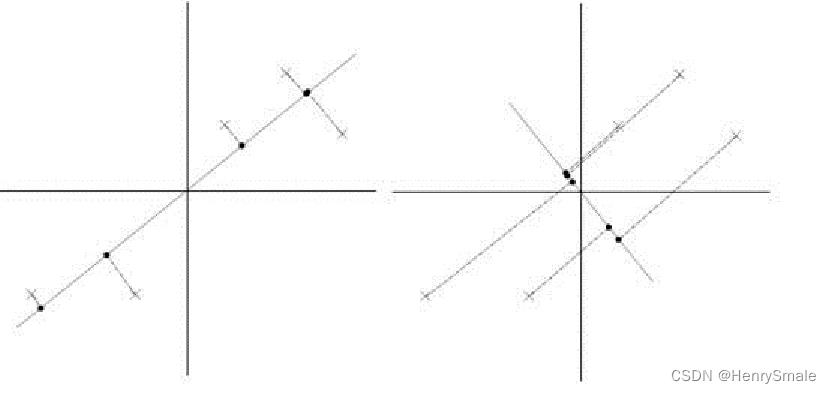
图 1中, + 表示正例, - 表示负例. 问: A, B 分别为正例还是负例?
直观来看, 应将 A 预测为负例, B 预测为正例. 如果你有机器学习的基础, 还可以用 kNN, SVM 之类进行强行解释, 不过这些不重要.

图 2 在图 1 的基础上增加了很多实例, 但我们不知道它们为正还是负. 现在重新判断A, B 分别为正例还是负例?

直观来看, A 与正例通过很多未标记数据 “连接” 起来, 而 B 与负例也通过很多未标记数据 “连接” 起来. 因此, 这个图中, 我们愿意相信 A 为正例, B 为负例.
为什么未标记数据让我们改变了主意? 因为他们带来了 数据分布 的巨大改变.

2 主动学习

人机交互获得专家的指导.

2.1 基本概念

主动学习是人机交互支撑的学习场景.
动机. 要想获得良好的学习效果, 通常需要大量的带标签数据. 在有些领域, 标签易于获取; 但在另外的领域, 打标签是专家的事情, 耗时耗力. 能不能使用更少的标签, 训练良好的学习器呢?
基本要求. 交互式的学习场景. 即: 人类专家根据机器的指定, 对相应数据打标签.
归属. 可以看作半监督学习的一种, 因为训练数据的一部分提供了标签.

2.2 主动学习的几种具体场景

冷启动封闭世界主动学习. 有 500 个样本, 先都没有给标签. 现在专家答应给其中 100 个打标签, 但其它 400 个需要机器预测.
冷启动开放世界主动学习. 有 500 个样本, 先都没有给标签. 现在专家答应给其中 100 个打标签. 机器需要对另外的一些样本 (未知样本) 进行预测.
一般情况下的封闭世界主动学习. 有 500 个样本, 其中 20 个标签已知. 现在专家答应给 80 个打标签, 但其它 400 个需要机器预测.
一般情况下的开放世界主动学习. 自己补上.

2.3 主动学习的核心问题

哪些样本的标签更有价值?
代表性强的样本. 把数据进行聚类, 聚类中心的样本具有良好的代表性. 其它样本很可能与它有相同的标签. 用这种思想可以设计出"基于聚类的主动学习方法".
不确定性强的样本. 有些样本有墙头草的潜质, 难于界定正负. 如果知道它们的标签, 就可以使用 SVM 进行分类, 相应地, 这次样本可能成为支撑向量 (support vector).

3 代价敏感学习

我们还是来谈钱吧.

3.1 常见的几类代价

代价敏感学习是将代价作为输入与优化目标时的机器学习.
代价是基础数据, 与应用有紧密联系.

• 测试代价. 很多数据不是免费的, 如体检时, 测血常规花 20 元, 心电图花15 元, B 超花200 元. 这些代价被称为测试代价 (test cost).
• 标记代价. 在主动学习场景下, 请专家给数据打标签需要付钱, 如每个标签花费 100 元. 这被称为标记代价 (label cost).
• 误分类代价. 将患有流感的病人叫回家, 医院要赔偿 10,000 元, 即 c(FN)=10,000; 将没有流感的就诊者留着住院治疗, 医院要赔偿 500 元, 即 (FP)=500. 相应地, 可以给出一个误分类代价矩阵.
• 延迟代价. 不清楚就诊者是否患病, 让其留院观察, 就诊者的误工开销为 200 元.

3.2 典型的代价敏感学习问题

代价是一类数据, 而且与其它数据处于不同维度, 本质上与机器学习: 数据的类型应该放在一起讨论. 可以把它当成一副狗皮膏药, 与不同的机器学习问题结合, 形成相应的代价敏感学习问题.
代价敏感分类问题：

• 输入: 数据, 标签, 误分类代价矩阵;
• 输出: 分类器;
• 优化目标: 平均误分类代价.

对于二分类问题, 当c(FN)=c(FP)>0 时, 代价敏感二分类问题退化为最大化准确率的二分类问题 (即不考虑代价).

代价敏感冷启动封闭世界主动学习问题：
输入: 数据, 标记代价, 误分类代价矩阵;
输出: 查询的标签, 分类器, 以及相应的预测值;
优化目标: 总代价;
假设总共有 800 个样本, 如果全让专家 (主治医生) 来打标签, 就要花 800×100=80,000 元. 正确的做法是让专家给某些重要样本打标签, 建立一个好的分类器, 冒着一定的误分类的风险, 对其它样本打标签.

测试代价敏感的特征选择问题：
输入: 数据, 标签, 各特征的测试代价;
输出: 特征子集;
优化目标: 最小化特征子集的测试代价之和.
约束条件: 特征子集与特征全集有相同的信息.
单位需要到组织 200 名 45 - 55 周岁的职工到医院进行体检, 确定检测的项目 (体检套餐) 就是一个测试代价敏感的特征选择问题.

3.3 解决数据不平衡问题是伪代价敏感学习

首先要明确两点：

• 代价作为基础数据, 都应该事先给出, 要么专家给出, 要么制度给出. 它们必须是输入, 而绝不会是输出 (被机器学习出来). 这是常识;
• 代价敏感学习的优化目标必须由代价定义, 而不应该是准确率之类.

一种常见的、错误的代价敏感学习概念如下: 由于数据中正负样本不平衡 (如1:99), 导致学习器偏向负样本. 为此, 将正例数量扩充至99 倍, 这样比例就变成 1:1, 可以愉快地进行学习了.

考虑两种情况：

• 正例表示有病 (如前段时间的新冠), 负例表示没病, 正例数远远少于负例数. 增加正例的比例, 分类器就会把更多的测试样本判断为正. 这样看起来好像是有道理的: 将大量负例隔离, 只为防止正例被漏掉在外传播;
• 正例数远远大于负例数. 这时候平衡正负例数量没有任何意义, 让所有人在家休息吃药不好吗?
  即使是第一种情况, 强行将比例变成1:1 也是不对的. 如果将c(FN):c(FP)=50, 即将正样本漏掉的代价很大, 这样才有利于把影响巨大的正样本找出来.

数据不平衡在现实很常见.
在极限多标签学习中, 正标签所占比例可以小到 0.1% 以下, 这时可以采用如下几种方式:

• 使用F1等评价指标;
• 使用基于序的评价指标.

反正不可以在没有代价数据的时候谈论代价敏感学习, 更不可以从数据中“学习”出各种代价设置. 再强调一遍: 作为“设置”, 它只可以是输入, 不可以是输出!

4 多标签学习

既感冒又肠炎, 真是一个悲伤的故事.

4.1 基本概念

多标签学习从标签个数上来扩展数据模型, 进一步还有标签分布学习.
将训练数据的标签表示为 $\mathbf{Y}$.

• 二分类问题: $\mathbf{Y}\in {-1,+1}^n$或者 $\mathbf{Y}\in {0,1}^n$.
• 多分类问题: $\mathbf{Y}\in {1,2,\dots ,k}^n$, 其中 $k$ 为类别数.
• 多标签学习问题: $\mathbf{Y}\in {0,1}^{n\times l}$, 其中 $l$为标签数. 这时$\mathbf{Y}$ 是一个布尔矩阵. 假设第 3 个标签表示猫, 则它为 1 的时候, 说明图片里有猫, 否则没有. 当$l<100$ 时, 称为多标签学习问题; 但 $l\ge 100$ 时 (这个尺度我也不好把握), 可以称为极限多标签学习问题.
• 标签分布学习问题: $\mathbf{Y}\in [0,1{]}^{n\times l}$. 这时$\mathbf{Y}$ 是一个小数矩阵 (每个数表示概率, 或者模糊数学中的隶属度).

这几个概念都是从标签的角度来定义的.

4.2 线性方案

数据矩阵$\mathbf{X}\in {\mathbb{R}}^{n\times m}$，标签矩阵 Y ∈ { 0 , 1 } n × l \mathbf{Y} \in \{0, 1\}^{n \times l} Y∈{0,1}n×l, 则可以学习权重矩阵$\mathbf{W}\in {\mathbb{R}}^{m\times l}$, 使得
$$\mathbf{XW}\approx \mathbf{Y}.$$
这种方案中, $\mathbf{W}$的第 $i$ 列对应于第 $i$ 个标签, 无法利用标签相关性.

4.3 主要应对的问题

标签相关性. 例如, 从训练数据看, 有猫和狗的时候, 多半也有老鼠. 根据这种规律就可以把一些图片中不明显的老鼠找出来. 如何有效利用标签相关性, 是多标签学习的核心问题.
标签稀疏性. 共有 100 种可能的动物, 但每张图片里一般只出现 1–5 种, 或者某些动物仅在少于 10 张图片里出现. 在极限多标签中, 标签稀疏性可能低于1%.
数据稀疏性. 数据的多个属性值为空, 或者无效. 在极限多标签中很严重.

5 多示例学习

我知道某堆蘑菇里有些有毒, 但不清楚是哪几个.

5.1 基本概念

多示例学习按照“包-样本”的方式组织数据, 并在包的级别上给标签.
与多标签学习类似, 多示例学习从数据的角度进行概念的扩展.
一个数据集由若干包 (bag) 组成, 每个包有若干示例 (即样本、对象, sample). 如果某个包中含有至少一个正样本, 则它为正包, 否则为负包.
说明:

• 由于标签打给包的, 最终可能也不知道具体的样本是正是负.
• 在进行预测的时候, 也仅给包打标签.
• 如果每个包仅有一个示例, 则退化为经典的机器学习.

5.2 常见方案

包映射. 将一个包映射为一个对象.
新的距离计算方式. 两个包的距离可以定义为:

• 最近点对的距离;
• 最远点对的距离;
• 包重心之间的距离.