一、梯度消失现象
当神经网络的输入值较大或较小时,其导数(梯度)都会接近于0。在反向传播过程中,这些微小的梯度经过多层网络逐层传递时,会不断被乘以权重矩阵(权重通常小于1),进一步导致梯度值缩小,直至几乎消失。这种现象称为“梯度消失”,它会使深度神经网络的学习过程变得极其缓慢,甚至无法有效训练深层网络。
二、Sigmoid激活函数
Sigmoid函数的公式为。其输出范围是(0,1)形状呈“S”型,两端趋于平缓,中间部分斜率较大。当输入值x非常大或者非常小的时候,Sigmoid函数的导数接近于0。
- 当x → -∞时,σ(x) → 0,σ'(x) → 0
- 当x → ∞时,σ(x) → 1,σ'(x) → 0
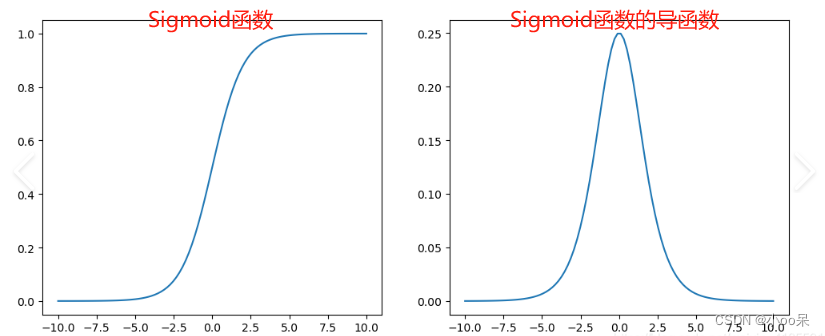
导致这一现象的原因在于Sigmoid函数的导数表达式为。当
非常接近0或者1时,
会迅速接近0,即梯度几乎消失。
三、Tanh激活函数
Tanh函数的公式为。取值在-1到1之间,图像形状类似拉伸的“S”形和Sigmoid函数很类似,其实Tanh函数相当于Sigmoid函数的平移
- 当x → -∞时,tanh(x) → -1,tanh'(x) → 0
- 当x → ∞时,tanh(x) → 1,tanh'(x) → 0

当输入值x的绝对值很大时,函数值也趋向于饱和(-1或1)。它的导数是,当tanh(x)非常接近-1或1时,tanh'(x)会迅速趋近于0,即梯度几乎消失。