论文信息
题目:Crowd-Robot Interaction:Crowd-aware Robot Navigation with Attention-based Deep Reinforcement Learning
作者:Changan Chen, Y uejiang Liu
代码地址:https://github.com/vita-epfl/CrowdNav
来源:arXiv
时间:2019
Abstract
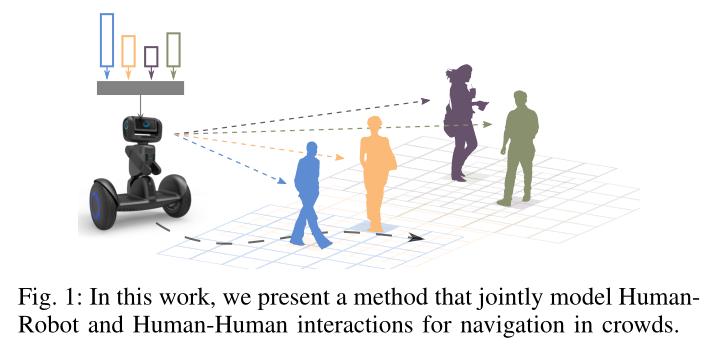
对于在拥挤空间中运行的机器人来说,以有效且符合社会规范的方式进行移动是一项重要但具有挑战性的任务。最近的工作显示了深度强化学习技术在学习社会合作政策方面的力量。然而,随着人群的增长,他们的合作能力会下降,因为他们通常将问题放松为单向人机交互问题。在这项工作中,我们希望超越一阶人机交互,并更明确地模拟人群与机器人交互(CRI)。
我们建议
(i)重新思考与自注意力机制的成对交互
(ii)在深度强化学习框架中联合建模人与机器人以及人与人的交互。我们的模型捕捉了密集人群中发生的人与人的互动,这间接影响了机器人的预期能力。
Introduction
遵守社交礼仪导航是一项具有挑战性的任务。
由于代理(例如人类)之间的通信并不广泛,因此机器人需要感知和预测人群的演变,这可能涉及复杂的相互作用(例如排斥/吸引)。轨迹预测方面的研究工作提出了几种手工或数据驱动的方法来模拟智能体之间的交互[12]-[15]。然而,将这些预测模型整合到决策过程中仍然具有挑战性。
作为替代方案,强化学习框架已用于训练计算高效的策略,这些策略隐式编码代理之间的交互和合作。尽管最近的工作[19]-[22]取得了重大进展,但现有模型仍然受到两个方面的限制:
i)人群的集体影响通常通过成对相互作用的简化聚合来建模,例如最大最小运算符[19]或LSTM[22],它们可能无法完全表示所有交互;
ii)大多数方法侧重于人类与机器人的单向交互,但忽略了可能间接影响机器人的人群内的交互。这些限制降低了复杂和拥挤场景中协作规划的性能
Background
Related Work
早期的工作主要利用精心设计的交互模型来增强机器人导航的社交意识。
一项开创性的工作是社会力[23]-[25],它已成功应用于模拟和现实环境中的自主机器人[26]-[28]。
另一种名为交互高斯过程(IGP)的方法将每个智能体的轨迹建模为单独的高斯过程,并提出一个交互势项来耦合单独的 GP 进行交互 [18]、[29]、[30]。在多智能体设置中,相同的策略应用于所有智能体,RVO [5] 和 ORCA [6] 等反应方法在相互假设下寻求联合避障速度。这些模型面临的主要挑战是它们严重依赖手工制作的功能,并且不能很好地泛化到各种人群合作的场景。
另一项工作使用模仿学习方法从期望行为的示范中学习政策。 [31]-[33] 中通过直接模仿专家演示来开发映射各种输入(例如深度图像、激光雷达测量和本地地图)以控制操作的导航策略。除了行为克隆之外,[10]、[11]、[34] 中还使用了逆强化学习,使用最大熵方法从人类数据中学习潜在的合作特征。这些工作中的学习成果高度依赖于示范的规模和质量,这不仅消耗资源,而且限制了人类努力学习的政策的质量。在我们的工作中,我们采用模仿学习的方法来热启动我们的模型训练。
强化学习(RL)方法在过去几年中得到了深入研究,并应用于各个领域,因为它开始在视频游戏中取得优异的性能[35]。在机器人导航领域,最近的工作已经使用强化学习从原始观察中学习静态和动态环境中的感觉运动策略[21]、[36],并利用代理级状态信息学习社会合作策略[19]、[20] ,[22]。为了处理不同数量的邻居,[19]中报告的方法通过最大最小操作从两个智能体适应多智能体情况,该操作针对人群的最坏情况采取最佳行动。后来的扩展使用 LSTM 模型按照与机器人的距离相反的顺序顺序处理每个邻居的状态 [22]。与这些简化相反,我们提出了一种新颖的神经网络模型来明确捕捉人群的集体影响。
Problem Formation
我们考虑一个导航任务,其中机器人穿过 n 个人的人群向目标移动。这可以表述为强化学习框架中的顺序决策问题[19]、[20]、[22]。
对于每个智能体(机器人或人类),位置 p = [ p x , p y ] p = [p_x, p_y] p=[px,py]、速度 v = [ v x , v y ] v = [v_x,v_y] v=[vx,vy] 和半径 r r r 可以被其他智能体观察到。机器人还知道其不可观察的状态,包括目标位置 p g p_g pg 和首选速度 v p r e f v_{pref} vpref 。我们假设机器人的速度 v t v_t vt 可以在动作命令 a t a_t at 之后立即达到,即 v t = a t v_t = a_t vt=at。令 s t s_t st 表示机器人的状态, w t = [ w t 1 , w t 2 , . . . , w t n ] w_t = [w^1_t ,w^2_t , . .. ,w^n_t] wt=[wt1,wt2,...,wtn]表示人类在时间 t t t的状态。机器人导航的关节状态定义为 s t j n = [ s t , w t ] s^{jn}_t = [s_t,w_t] stjn=[st,wt]。

我们遵循[19]、[20]中定义的奖励函数的公式,该函数奖励任务成就,同时惩罚碰撞或不舒服的距离

Value Network Training
价值网络通过时差法、标准经验回放和固定目标网络技术进行训练[19],[35]。如算法 1 中所述,模型首先使用一组演示者经验(第 1-3 行)通过模仿学习进行初始化,然后根据交互经验进行细化(第 4-14 行)。与之前的工作[19]、[20]的一个区别是,第7行中的下一个状态S jn t+1是通过查询环境的真实值而不是用线性运动模型近似来获得的,从而减轻了系统动力学问题训练。在部署期间,转移概率可以通过轨迹预测模型[12]、[13]、[15]来近似。

为了有效地解决问题(1),价值网络模型需要准确逼近隐式编码智能体之间社会合作的最优价值函数V*。该轨道之前的工作并未完全模拟人群互动,这降低了人口稠密场景的价值估计的准确性。在以下部分中,我们将提出一种新颖的人群机器人交互模型,该模型可以有效地学习在拥挤的空间中导航。
Approach
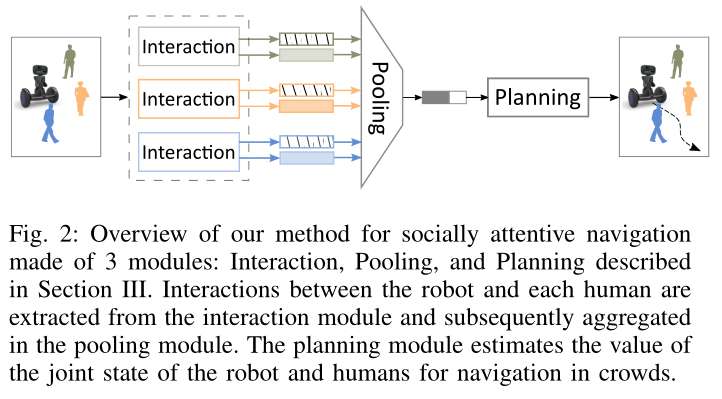
当人类行走在人口稠密的场景中时,他们会通过预测附近邻居的行为来与他人合作,特别是那些可能参与未来某些互动的邻居。这促使我们设计一个模型,可以计算相对重要性并编码邻近代理的集体影响,以实现社交合规导航。受社交池[13]、[15]和注意力模型[14]、[44]-[48]的启发,我们引入了一个由三个模块组成的社交注意力网络:
• Interaction module:显式地建模人机交互,并通过粗粒度局部映射对人机交互进行编码。
• Pooling module:通过自注意力机制将交互聚合成固定长度的嵌入向量。
• Planning module:估计机器人与人群的关节状态对于社交导航的价值。
Parameterization
我们遵循[19]、[22]中以机器人为中心的参数化,其中机器人位于原点,x轴指向机器人的目标。机器人和行走人变换后的状态为:

Interaction Module
每个人都会对机器人产生影响,同时也会受到他/她的邻居的影响。对人类之间的所有交互对进行显式建模会导致 O(N2) 复杂性 [14],这对于在密集场景中扩展的策略来说在计算上是不可取的。我们通过引入一个成对交互模块来解决这个问题,该模块显式地模拟人机交互,同时使用局部地图作为人机交互的粗粒度表示。
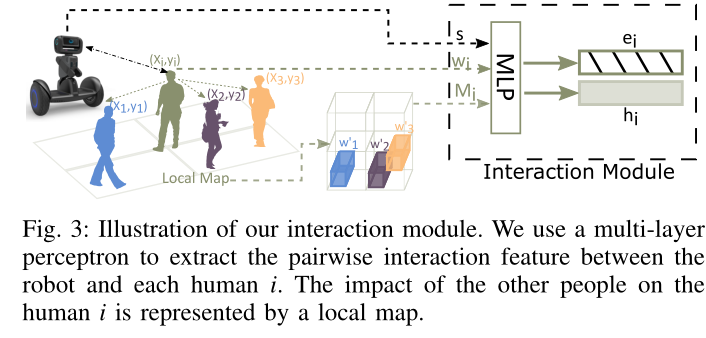
给定大小为 L 的邻域,我们构造一个以每个人 i 为中心的 L × L × 3 地图张量 M i M_i Mi 来编码邻居的存在和速度,在图 3 中称为局部地图:

我们使用多层感知器(MLP)将人类 i 的状态和地图张量 M i M_i Mi 以及机器人的状态一起嵌入到固定长度的向量 e i e_i ei 中:

嵌入向量 e i e_i ei 被馈送到后续的 MLP 以获得机器人和人 i 之间的成对交互特征:
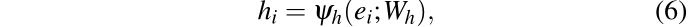

Pooling Module
由于不同场景中周围人群的数量可能会有很大差异,因此我们需要一个能够将任意数量的输入处理为固定大小的输出的模型。
Everett 等人 [22] 提出将所有人类的状态按照与机器人的距离降序依次输入 LSTM [49]。然而,最接近的邻居具有最强影响力的基本假设并不总是正确的。其他一些因素,例如速度和方向,对于正确估计邻居的重要性也至关重要,这反映了该邻居如何潜在地影响机器人的目标获取。利用自注意力机制的最新进展,其中序列中某个项目的注意力是通过查看序列中的其他项目来获得的[44]、[46]、[50],我们提出了一个社交注意力池模块以数据驱动的方式了解每个邻居的相对重要性以及人群的集体影响。
交互嵌入 e i e_i ei 转换为注意力分数 α i α_i αi 如下:
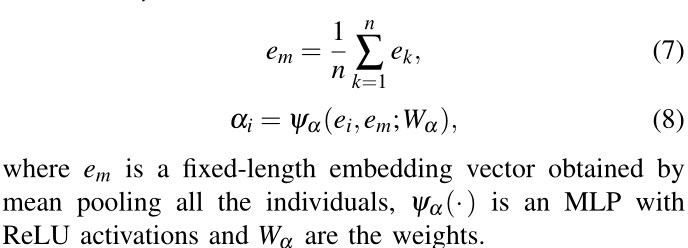
给定每个邻居 i 的成对交互向量 h i h_i hi 和相应的注意力分数 α i α_i αi,人群的最终表示是所有对的加权线性组合:
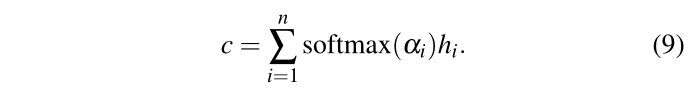
Planning Module
基于人群 c 的紧凑表示,我们构建了一个规划模块,用于估计合作规划的状态值 v:
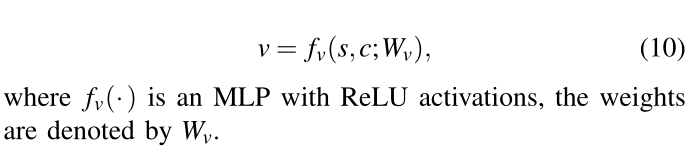
Implementation Details
局部地图是一个以每个人为中心的 4 × 4 网格,每个网格的边长为 1m 。函数 ϕ e ( ⋅ ) 、 ψ h ( ⋅ ) 、 ψ α ( ⋅ ) 、 f v ( ⋅ ) \phi_e(·)、ψ_h(·)、ψ_α(·)、f_v(·) ϕe(⋅)、ψh(⋅)、ψα(⋅)、fv(⋅) 的隐藏单元分别为 (150,100)、(100,50)、(100,100)、(150,100,100)。
我们在 PyTorch [51] 中实现了该策略,并使用 Adam [52] 以 100 的批量大小对其进行训练。对于模仿学习,我们使用 ORCA 收集了 3k 集演示,并以学习率 0.01 训练了策略 50 个时期。对于强化学习,学习率为0.001,折扣因子γ为0.9。 ε-贪婪策略的探索率在前 5k 集中从 0.5 线性衰减到 0.1,并在剩余 5k 集中保持 0.1。 RL 训练在 i7-8700 CPU 上花费了大约 10 个小时。
这项工作假设机器人具有完整的运动学,即它可以向任何方向移动。动作空间由 80 个离散动作组成:5 个速度在 (0, vpre f ] 之间呈指数分布,16 个方向在 [0, 2π) 之间均匀分布。
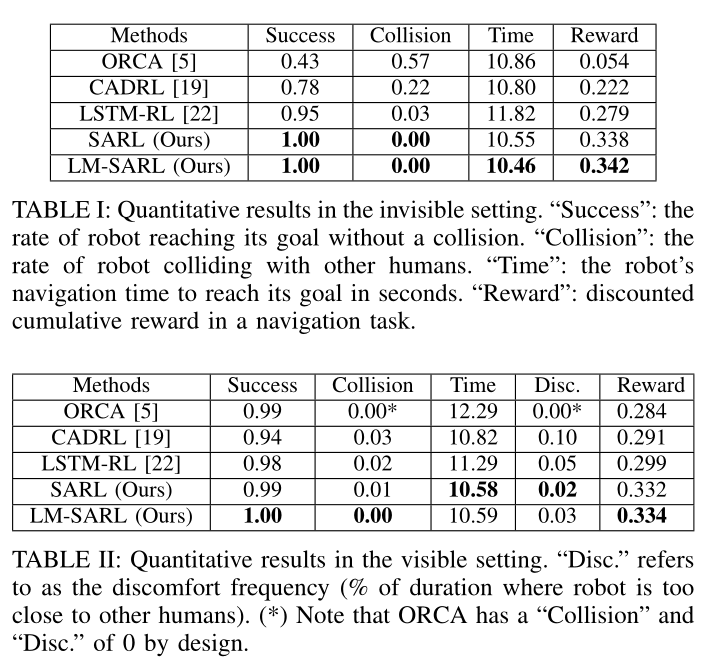
Experiments